Abstract
The study of heat transport has the potential to reveal new insights into the physics of mesoscopic systems. This is especially true of those that show the integer quantum Hall effect1, in which the robust quantization of Hall currents limits the amount of information that can be obtained from charge transport alone2. As a consequence, our understanding of gapless edge excitations in these systems is incomplete. Effective edge-state theory describes them as prototypical one-dimensional chiral fermions3,4—a simple picture that explains a large body of observations5 and suggests the use of quantum point contacts as electronic beam splitters to explore a variety of quantum mechanical phenomena6,7,8. However, this picture is in apparent disagreement with the prevailing theoretical framework, which predicts in most situations9 extra gapless edge modes10. Here, we present a spectroscopic technique that addresses the question of whether some of the injected energy is captured by the predicted extra states, by probing the distribution function and energy flow in an edge channel operated out-of-equilibrium. Our results show it is not the case and therefore that regarding energy transport, quantum point contacts do indeed behave as optical beam splitters. This demonstrates a useful new tool for heat transport and out-of-equilibrium experiments.
Similar content being viewed by others
Main
The integer quantum Hall effect, discovered nearly thirty years ago1, has recently experienced a strong revival driven by milestone experiments towards quantum information with edge states7,11,12. Beyond Hall currents, new phenomena have emerged that were unexpected within the free one-dimensional chiral fermions (1DCFs) model. The ongoing debate triggered by electronic Mach–Zehnder interferometer experiments7,13,14,15 vividly illustrates the gaps in our understanding. Coulomb interaction is seen as the key ingredient. In addition to its most striking repercussion, the fractional quantum Hall effect16, the edge reconstruction turns out to have deep implications on edge excitations. This phenomenon results from the competition between Coulomb interaction that tends to spread the electronic fluid, and the confinement potential: as the latter gets smoother, the non-interacting edge becomes unstable17. Theory predicts new branches of gapless electronic excitations in reconstructed edges10,18, which breaks the mapping of an edge channel onto 1DCFs and, possibly, the promising quantum optics analogy. For most edges realized in semiconductor heterojunctions (except by cleaved edge overgrowth19), edge reconstruction results in wide compressible edge channels separated by narrow incompressible strips9 and the new excited states are overall neutral internal charge oscillations across the edge channels’ width10.
In practice, the predicted extra neutral modes are transparent to Hall currents. More surprisingly, a linear I–V characteristic is frequently observed for tunnel contacts (different behaviours were also reported, for example, ref. 20), whereas a nonlinear characteristic is predicted21,22,23. This contradiction is resolved by assuming ad-hoc that only rigid displacements of compressible edge channels are excited by tunnel events, and not internal excitations10,21,22,24. The rigid displacement model arguably relies on the overriding strength of Coulomb interaction that tends to orthogonalize bare tunnelling electrons and correlated electronic fluids24. However, the above argument does not hold at arbitrary transmission probabilities, where several electron processes occur. Therefore, the role of predicted internal excitations has to be determined experimentally. The present work provides such a test. An edge channel is driven out-of-equilibrium with a quantum point contact (QPC) of arbitrary transmission, possibly exciting internal modes. A short distance away, the resulting energy distribution f(E) is measured with a tunnel-coupled quantum dot expected to probe only rigid displacement excitations, hereafter called quasiparticles. Consequently, the amount of energy injected into internal modes at the QPC would appear as an energy loss in f(E).
Measurements of the energy distribution in mesoscopic devices were first carried out in 1997 on metallic circuits using a superconducting tunnel probe25. In two-dimensional electron-gas systems, non-Fermi energy distributions could not be measured because transferring the techniques developed for metal circuits is technically challenging (although hot electrons have been detected, for example, ref. 26). Regarding the quantum Hall regime, the state of the art is the very recent qualitative probe of heating27. Here, we demonstrate that f(E) can be fully extracted from the tunnel current across a quantum dot. In the sequential tunnelling regime, the discrete electronic levels in a quantum dot behave as energy filters28, as previously demonstrated with double quantum dots29. Assuming a single active quantum-dot level of energy Elev, and ignoring the energy dependence of tunnel rates and tunnelling density of states in the electrodes, the quantum-dot current reads

where the subscript S (D) refers to the source (drain) electrode; fS,D are the corresponding energy distributions and IQDmax is the maximum quantum-dot current. In practice, fS,D are obtained separately by applying a large enough source–drain voltage (Fig. 1a,b) and the probed energy Elev=E0−e ηGVG is swept using a capacitively coupled gate biased at VG, with ηG being the gate voltage-to-energy lever arm and E0 an offset. Raw data ∂ IQD/∂ VG measured by lock-in techniques are proportional to ∂ fD,S(E)/∂ E.
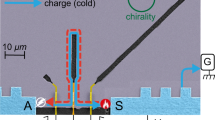
a, Schematic description of the energy distributions’ fD,S(E) spectroscopy with a single active electronic level of tunable energy Elev(VG) in the quantum dot. b, The current IQD (∂ IQD/∂ VG) is proportional to fS(E)−fD(E) (∂(fS(E)−fD(E))/∂ E) ignoring variations in tunnel rates and tunnelling density of states. c, Electron-beam micrograph of the sample. Surface metal gates appear brighter. Electronic excitations propagate anticlockwise along two edge channels of the quantum Hall regime. The outer edge channel (solid white lines) is partly transmitted (dashed lines) across the QPC and the quantum dot. The inner edge channel (not shown) is always reflected. The QPC is used to drive out-of-equilibrium the drain outer edge channel. Gates partly covered by the insets are grounded and do not influence the electron paths. Left inset: Non-interacting electrons prediction for fD(E) in the outer edge channel at the output of the QPC. Right inset: Equilibrium Fermi function fS emitted by a cold ground.
A tunable non-Fermi energy distribution is generated in an edge channel with a voltage-biased QPC. Similar set-ups were used previously to create imbalanced electron populations between co-propagating edge channels30, each characterized by a cold Fermi distribution. Only in a very recent experiment27 was an edge channel heated up. Beyond heating, f(E) is here controllably tuned out-of-equilibrium. Let us consider one edge channel and assume it can be mapped onto non-interacting 1DCFs. According to the scattering approach5, the energy distribution at the output of a QPC of transmission τ is a tunable double step (Fig. 1c, left inset)

where fD1 (fD2) is the equilibrium Fermi distribution function in the partially transmitted (reflected) incoming edge channel of electrochemical potential shifted by e VD1 (e VD2). In the presence of edge reconstruction, the above energy distribution applies to the quasiparticles if internal modes are not excited at the QPC. On the other hand, if internal modes are excited, there are no theoretical predictions because a QPC is very difficult to treat non-perturbatively in their natural bosonic formalism.
The sample shown in Fig. 1c was tailored in a two-dimensional electron gas realized in a GaAs/Ga(Al)As heterojunction, set to filling factor two and measured in a dilution refrigerator of base temperature 30 mK. The experiment detailed here focuses on the outer edge channel represented as a white line. The inner edge channel (not shown) is fully reflected by the QPC and the quantum dot. We checked that charge tunnelling between edge channels is negligible along the 0.8 μm propagation length from the QPC to the quantum dot.
We first carry out a standard nonlinear quantum-dot characterization28 (Fig. 2, top left inset). The two large signal stripes are frontiers of consecutive Coulomb diamonds and are accounted for by a single active quantum-dot level. Small contributions of three extra levels of relative energies {−95,30,130} μeV are also visible. The lever arm extracted from the stripes’ slopes is ηG≃0.052±9%.
Temperatures Tfit are obtained by fitting the quantum-dot drain dip and quantum-dot source peak in ∂ IQD/∂ VG (respectively, left and right peaks in bottom right inset), and from the single ∂ IQD/∂ VD peak at VD=0 (raw data not shown) with ηG=0.057. We assumed a single active level in the quantum dot and Fermi energy distributions in source and drain. Errors within T±10% are enclosed between the dashed lines. Top left inset: Surface plot of ∂ IQD/∂ VG (negative is brighter, positive darker) measured at T=30 mK for an outer (inner) drain edge channel biased at VD (−88 μV). The intense stripes’ slopes yield ηG=0.052±9%. The enclosed dashed lines outline the small contributions of other electronic levels. Bottom right inset: ∂ IQD/∂ VG measured at VD−VS=−88 μV for several temperatures.
Then, we test the spectroscopy with known Fermi functions by measuring ∂ IQD/∂ VG(VG) at VD1=VD2=−88 μV for several temperatures (Fig. 2, bottom right inset). By fitting these data with equation (1) using Fermi functions, we extract a fit temperature scaled by the lever arm Tfit/ηG. The value ηG=0.057, compatible with the nonlinear quantum-dot characterization, is found to reproduce best the mixing-chamber temperature T with Tfit. The drain and source fit temperatures are shown in Fig. 2, together with Tfit obtained using the standard procedure28 from ∂ IQD/∂ VD(VG) at VD≃0. We find deviations mostly within ±10% (dashed lines in Fig. 2) except for a saturation at Tfit≈50 mK possibly owing to a higher electronic temperature. In the following, we use ηG=0.057 obtained here in the same experimental configuration as to measure unknown f(E)s.
Electrons are now driven out-of-equilibrium in the drain outer edge channel. In the following, the electrode D2 and the inner drain edge channel are voltage biased at VD2=−88 μV and the source edge channels are emitted by a cold ground.
First, the bias voltage across the QPC is set to δ VD≡VD1− VD2=36 μV and its conductance GQPC=τ e2/h is tuned by applying VQPC to the bottom left gate in Fig. 1c (see Fig. 3a). Note that at 30 mK, we find the transmission τ is constant within 2% with the QPC voltage bias below 36 μV. Typical sweeps ∂ IQD/∂ VG(VG) and the corresponding fD(E) are shown in Fig. 3b and e, respectively. The quantum-dot drain negative contribution transforms from a single dip at τ={0,1} into two dips separated by a fixed gate voltage and with relative weights that evolve monotonously with τ∈]0,1[. The solid lines are fits with equation (2) using for fD1,D2 two Fermi functions shifted by a fixed energy and weighted by the factors τfit and 1−τfit. The values of τfit are found to deviate by less than 0.03 from the measured transmission τ (Fig. 3c), in accurate agreement with the free 1DCF model. The plus symbols in Fig. 3 correspond to data obtained in a second cooldown.
The QPC’s voltage bias is here fixed to δ VD≡VD1−VD2=36 μV. The data shown as plus symbols in c,d were obtained in a second cooldown with a renewed ηG=0.059±7%. a, Measured GQPC versus VQPC applied to the lower left metal gate in Fig. 1c. The symbols are data points obtained during the corresponding edge-channel spectroscopy. The solid line was measured earlier with δ VD=0. b, Measured ∂ IQD/∂ VG (symbols) for the quantum-dot drain contribution (data have been aligned in VG and normalized to IQDmax). The two dips correspond to a double-step energy distribution fD(E). c, The symbols are τfit obtained from fits of the data (solid lines in b) assuming fD(E) is the weighted sum of two Fermi functions. We find an accurate agreement with the non-interacting 1DCF model prediction τfit=GQPCh/e2. d, Generalized non-equilibrium temperature (symbols, see text) extracted from the data and theoretical prediction for free 1DCFs (solid line). The error bars are dominated by uncertainties on ηG. e, Energy distributions obtained by integrating the data in b.
In a second step, the QPC transmission is fixed to τ≈0.5 and the bias voltage δ VD is changed. Typical raw data are shown in Fig. 4a. These were obtained in a third cooldown with a quantum dot renewed by the thermal cycle showing no signs of extra quantum-dot levels in the probed energy range. The single dip in the quantum-dot drain contribution (bright) at δ VD=0 splits into two similar dips that are separated by a gate-voltage difference proportional to δ VD. In contrast, the quantum-dot source peak (dark) is mostly unchanged but slowly drifts parallel to one quantum-dot drain dip owing to the capacitive coupling between the drain and the quantum dot. In the first cooldown, VD1 was kept within [−106,−34] μV to minimize complications related to extra quantum-dot levels (lower bound) and to ensure well-separated source and drain contributions (upper bound). The symbols in Fig. 4b and e are, respectively, data and extracted fD(E) for the quantum-dot drain contribution at δ VD={−18,0,18,27,36,45,54} μV and τ=0.58. The solid lines in Fig. 4b are fits with equation (2) using the measured τ and for fD1,D2 two Fermi functions shifted in energy by the fit parameter −e ηGδ VG. The resulting ηGδ VG are plotted as symbols versus δ VD in Fig. 4c. Those obtained in the third cooldown are shown as purple star symbols using the renewed lever arm ηG=0.062. We find ηGδ VG≃δ VD as expected from the non-interacting 1DCF model. Deviations are always smaller than 8 μV (5 μV) for the first (third) cooldown, a reasonable agreement regarding uncertainties in ηG of ±10% (±5%).
The QPC’s conductance is here fixed to GQPC≈0.5e2/h. The data in a and the purple star symbols in c and d were obtained in a third cooldown with a renewed ηG=0.062±5%. a, Surface plot of ∂ IQD/∂ VG(δ VD,VG). The quantum-dot drain contribution (brighter) splits into two similar dips separated by a gate-voltage difference proportional to δ VD. b, Measured ∂ IQD/∂ VG (symbols) for the quantum-dot drain contribution. Data have been shifted vertically for clarity, and horizontally to align the peak corresponding to the fixed potential VD2. The solid lines are fits assuming fD(E) is the weighted sum of two Fermi functions. c, The symbols are the fit parameters ηGδ VG. The solid line is the prediction for non-interacting 1DCFs. d, Generalized non-equilibrium temperature (symbols) and theoretical prediction for free 1DCFs (solid line). The good data–prediction agreement demonstrates that internal modes are not excited at the QPC within our experimental accuracy. e, Energy distributions obtained by integrating the data in b.
In the two experiments above, we found the measured quasiparticle f(E)s verify predictions of the scattering approach. To establish the QPC/beam-splitter analogy one also needs to demonstrate that internal edge-channel modes are not excited. A direct test consists of extracting the quasiparticle heat current JEqp from the data, and comparing it with the full edge-excitations’ heat current JE obtained from power-balance considerations (see Supplementary Information for details):

The cancellation v ν=1/h of velocity (v) and density of states per unit length and energy (ν) that applies to the 1DCF quasiparticles permits us to obtain JEqp from the measured f(E) without any sample-specific parameters:

where μ is the electrochemical potential and θ(E) is the step function. Consequently, we measure quantitatively the quasiparticle heat current. The result of this procedure is shown as symbols in Figs 3d and 4d using the generalized non-equilibrium temperature  together with the prediction
together with the prediction  if none of the injected power is carried on by internal modes (solid lines). We find a good agreement Tqp≃T1DCF without fitting parameters and essentially in or close to error bars. Hence, within our experimental accuracy, the propagative internal modes do not contribute to heat transport and therefore are not excited. Note that the relatively small observed deviations are cooldown dependent, which suggests that the quantum-dot detector is responsible for these deviations. Indeed, the data can be more accurately accounted for including a second active quantum-dot level (see Supplementary Information). Last, preliminary data show a significant energy redistribution with the inner edge channel for propagations longer than 2 μm in the probed energy range. Therefore, the observed small discrepancies could also result from the finite 0.8 μm propagation length.
if none of the injected power is carried on by internal modes (solid lines). We find a good agreement Tqp≃T1DCF without fitting parameters and essentially in or close to error bars. Hence, within our experimental accuracy, the propagative internal modes do not contribute to heat transport and therefore are not excited. Note that the relatively small observed deviations are cooldown dependent, which suggests that the quantum-dot detector is responsible for these deviations. Indeed, the data can be more accurately accounted for including a second active quantum-dot level (see Supplementary Information). Last, preliminary data show a significant energy redistribution with the inner edge channel for propagations longer than 2 μm in the probed energy range. Therefore, the observed small discrepancies could also result from the finite 0.8 μm propagation length.
Overall, we demonstrate that QPCs in the quantum Hall regime are tunable electrical beam splitters for one-dimensional fermions, that is, rigid edge-channel displacements, (1) by comparing the energy distribution at a QPC output with predictions of the scattering approach5, and (2) by showing that internal edge-channel modes are not excited. This does not only rule out non-ideal QPC behaviours to explain the surprising phenomena observed on electronic Mach–Zehnder interferometers7,13,14,15, it also establishes a solid ground for future quantum information applications with edge states. Finally, an essential part of this work is the demonstration of a new technique to measure the fundamental energy-distribution function. It makes f(E) accessible for most systems where quantum dots can be realized. We expect it will trigger many new experiments dealing with heat transport, out-of-equilibrium physics and quantum decoherence.
References
Klitzing, K. v., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Fertig, H. A. A view from the edge. Physics 2, 15 (2009).
Halperin, B. I. Quantized Hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 25, 2185–2190 (1982).
Wen, X.-G. Theory of the edges states in fractional quantum Hall effects. Int. J. Mod. Phys B 6, 1711–1762 (1992).
Büttiker, M. Absence of backscattering in the quantum Hall effect in multiprobe conductors. Phys. Rev. B 38, 9375–9389 (1988).
Ionicioiu, R., Amaratunga, G. & Udrea, F. Quantum computation with ballistic electrons. Int. J. Mod. Phys. B 15, 125–133 (2001).
Ji, Y. et al. An electronic Mach–Zehnder interferometer. Nature 422, 415–418 (2003).
Samuelsson, P., Sukhorukov, E. V. & Büttiker, M. Two-particle Aharonov–Bohm effect and entanglement in the electronic Hanbury Brown–Twiss setup. Phys. Rev. Lett. 92, 026805 (2004).
Chklovskii, D. B., Shklovskii, B. I. & Glazman, L. I. Electrostatics of edge channels. Phys. Rev. B 46, 4026–4034 (1992).
Aleiner, I. L. & Glazman, L. I. Novel edge excitations of two-dimensional electron liquid in a magnetic field. Phys. Rev. Lett. 72, 2935–2938 (1994).
Fève, G. et al. An on-demand coherent single-electron source. Science 316, 1169–1172 (2007).
Neder, I. et al. Interference between two indistinguishable electrons from independent sources. Nature 448, 333–337 (2007).
Roulleau, P. et al. Direct measurement of the coherence length of edge states in the integer quantum Hall regime. Phys. Rev. Lett. 100, 126802 (2008).
Litvin, L. V., Tranitz, H. P., Wegscheider, W. & Strunk, C. Decoherence and single electron charging in an electronic Mach–Zehnder interferometer. Phys. Rev. B 75, 033315 (2007).
Bieri, E. et al. Finite-bias visibility dependence in an electronic Mach–Zehnder interferometer. Phys. Rev. B 79, 245324 (2009).
Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
MacDonald, A. H., Yang, S. R. E. & Johnson, M. D. Quantum dots in strong magnetic fields: Stability criteria for the maximum density droplet. Aust. J. Phys. 46, 345–358 (1993).
Chamon, C. de C. & Wen, X. G. Sharp and smooth boundaries of quantum Hall liquids. Phys. Rev. B 49, 8227–8241 (1994).
Chang, A. M., Pfeiffer, L. N. & West, K. W. Observation of chiral Luttinger behavior in electron tunneling into fractional quantum Hall edges. Phys. Rev. Lett. 77, 2538–2541 (1996).
Roddaro, S., Pellegrini, V., Beltram, F., Pfeiffer, L. N. & West, K. W. Particle-hole symmetric Luttinger liquids in a quantum Hall circuit. Phys. Rev. Lett. 95, 156804 (2005).
Conti, S. & Vignale, G. Collective modes and electronic spectral function in smooth edges of quantum Hall systems. Phys. Rev. B 54, R14309–R14312 (1996).
Han, J. H. & Thouless, D. J. Dynamics of compressible edge and bosonization. Phys. Rev. B 55, R1926–R1929 (1997).
Yang, K. Field theoretical description of quantum Hall edge reconstruction. Phys. Rev. Lett. 91, 036802 (2003).
Zülicke, U. & MacDonald, A. H. Periphery deformations and tunneling at correlated quantum Hall edges. Phys. Rev. B 60, 1837–1841 (1999).
Pothier, H., Guéron, S., Birge, N. O., Esteve, D. & Devoret, M. H. Energy distribution function of quasiparticles in mesoscopic wires. Phys. Rev. Lett. 79, 3490–3493 (1997).
Heiblum, M., Nathan, M. I., Thomas, D. C. & Knoedler, C. M. Direct observation of ballistic transport in GaAs. Phys. Rev. Lett. 55, 2200–2203 (1985).
Granger, G., Eisenstein, J. P. & Reno, J. L. Observation of chiral heat transport in the quantum Hall regime. Phys. Rev. Lett. 102, 086803 (2009).
Kouwenhoven, L. P. et al. in Mesoscopic Electron Transport Series E: Applied Sciences Vol. 345 (eds Sohn, L. L., Kouwenhoven, L. P. & Schön, G.) 105–214 (Kluwer Academic, 1997).
van der Vaart, N. C. et al. Resonant tunneling through two discrete energy states. Phys. Rev. Lett. 74, 4702–4705 (1995).
van Wees, B. J. et al. Anomalous integer quantum Hall effect in the ballistic regime with quantum point contacts. Phys. Rev. Lett. 62, 1181–1184 (1989).
Acknowledgements
The authors gratefully acknowledge discussions with M. Buttiker, P. Degiovanni, C. Glattli, P. Joyez, A. H. MacDonald, F. Portier, H. Pothier, P. Roche and G. Vignale. This work was supported by the ANR (ANR-05-NANO-028-03).
Author information
Authors and Affiliations
Contributions
Experimental work and data analysis: C.A., H.l.S. and F.P.; nanofabrication: C.A. and F.P. with input from D.M.; heterojunction growth: A.C. and U.G.; theoretical analysis and manuscript preparation: F.P. with input from coauthors; project planning and supervision: F.P.
Corresponding author
Supplementary information
Supplementary Information
Supplementary Information (PDF 538 kb)
Rights and permissions
About this article
Cite this article
Altimiras, C., le Sueur, H., Gennser, U. et al. Non-equilibrium edge-channel spectroscopy in the integer quantum Hall regime. Nature Phys 6, 34–39 (2010). https://doi.org/10.1038/nphys1429
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1429
This article is cited by
-
Non-thermal Tomonaga-Luttinger liquid eventually emerging from hot electrons in the quantum Hall regime
Communications Physics (2023)
-
Direct determination of the topological thermal conductance via local power measurement
Nature Physics (2023)
-
Quasiparticle Andreev scattering in the ν = 1/3 fractional quantum Hall regime
Nature Communications (2023)
-
Quantized charge fractionalization at quantum Hall Y junctions in the disorder dominated regime
Nature Communications (2021)
-
Relaxation and revival of quasiparticles injected in an interacting quantum Hall liquid
Nature Communications (2020)