Main

Bound electron–hole particles, known as excitons, are fascinating objects in semiconductor nanostructures. In a quantum well with a thickness of the order of a few nanometres, the external motion of the exciton is quantized in the direction perpendicular to the well, whereas it is free within the plane of the well. When the quantum well is placed in a high-finesse microcavity, the strong-coupling regime between excitons and light is easily reached14, giving rise to exciton–photon mixed quasiparticles called polaritons, which are an interesting kind of two-dimensional composite boson. Thanks to their sharp dispersion, polaritons have a small effective mass (of the order of 10−5 times the free-electron mass) that allows the building of many-body coherent effects, such as Bose–Einstein condensation15,16, at a lattice temperature of a few kelvins. Furthermore, their partially excitonic character results in strong interactions between polaritons, which are expected to lead to the appearance of superfluid phenomena. Indirect evidence of superfluid motion in polariton systems has recently been reported through the observation of pinned quantized vortices9, Bogoliubov-like dispersions10 and pioneering experiments on polariton parametric oscillators11. Despite these remarkable works, a direct demonstration of exciton–polariton superfluidity is however still missing. In this Letter, we report the observation of superfluid motion of a quantum fluid of polaritons created by a laser in a semiconductor microcavity.

In our experiments, to probe superfluidity we study the perturbation that is produced in an optically created moving polariton fluid when a static defect is present in the flow path, as proposed in refs. 12, 13. This procedure is a direct application to the polariton system of the standard Landau criterion of superfluidity5, originally developed for liquid helium and recently applied to demonstrate superfluidity of atomic Bose–Einstein condensates (refs 17, 18). The flow without friction characteristic of a superfluid is demonstrated in the case of polaritons as a flow without scattering.

To explore the quantum fluid regime a complete control of three key parameters is needed: the in-plane momentum of polaritons (that is, the polariton flow velocity), the oscillation frequency of the polariton field, and its density. In this respect polaritons constitute an ideal system from the experimental point of view. The strength of the polariton–polariton interaction within the fluid can be controlled through the particle density, which in turn is changed in a precise way by adjusting the incident laser power. Their partially photonic character also allows the creation of polariton fluids with a well-defined oscillation frequency, ωp, which is that of the excitation laser, and with a well-defined linear momentum, kp, by choosing the angle of incidence θp (kp=(ωp/c)sinθp, where c is the light speed). The possibility of controlling the polariton fluid oscillation frequency is in stark contrast with equilibrium systems, such as atomic condensates, where the oscillation frequency of the condensate is fixed by the equation of state relating the chemical potential to the particle density3: owing to their relatively short lifetime (of the order of few picoseconds), the steady state of an excited microcavity results from the interplay between the pumping rate and the radiative as well as non-radiative losses. This feature results in much wider possibilities in the structure of the system’s spectrum of elementary excitations than in the equilibrium case12,13,19,20,21,22.

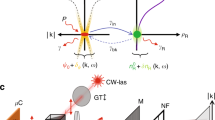
In our experiment, a polariton fluid is excited in a microcavity sample (see the Methods section), cooled at 5 K, with a circularly polarized beam from a frequency-stabilized, single-mode continuous-wave titanium:sapphire laser. The laser field continuously replenishes the escaping polaritons in the fluid. The beam is focused onto the sample in a spot of ∼100 μm in diameter with angles of incidence between 2.6∘ and 4.0∘ (Fig. 1a). The wavelength of the pump laser is around 836 nm, close to resonance with the lower polariton branch. The images of the surface of the sample (near-field emission) and of the far field in transmission configuration are simultaneously recorded on two different high-resolution CCD (charge-coupled device) cameras. With the use of a spectrometer and at low-power, off-resonance excitation, the characteristic parabolic lower-polariton dispersion can be observed, as shown in Fig. 1b.

Figure 1: Experimental set-up and polariton dispersion.
figure 1

a, Overview of the experimental excitation and detection conditions. b, Lower-polariton-branch dispersion in the linear regime as observed after non-resonant excitation. Points A and B denote the excitation energy and momentum corresponding to the results shown in Figs 2 and 3, respectively. c, Analytically calculated spectrum of excitations under low-power resonant pumping at the point indicated by the yellow dot for low pump momentum (point A in b). Injected polaritons can elastically scatter to the same energy states as those indicated by the green arrow. Ep refers to the energy of the pump beam. d, Spectrum of excitations under strong resonant pumping under the conditions of superfluidity— Fig. 2c-III, c-VI and d-III, d-VI—where the Landau criterion is fulfilled and injected polaritons cannot scatter owing to the absence of available final states at the energy of the pump. The red section demonstrates the strongly modified linear shape due to polariton–polariton interaction. e,f, Analytically calculated spectra for larger pump momentum (point B in b) at low and high density, respectively. At high density, corresponding to that of Fig. 3b-II, b-V and c-II, c-V, the linear spectrum of excitations results in cs<vp and the Čerenkov regime is attained.

Full size image

To study the propagation properties of the injected polariton fluid, the centre of the excitation spot is placed on top of a natural point-like defect present in the sample. Defects of different sizes and shapes appear naturally in the growth process of microcavity samples (see Supplementary Information). At low excitation power and quasiresonant excitation of the lower polariton branch, polariton–polariton interactions are negligible: in the near-field (real-space) images, the coherent polariton gas created by the laser is scattered by the defect and generates a series of parabolic-like wavefronts around the defect, propagating away from it, mostly in the upstream direction (Figs 2c-I and 3b-I). They result from the interference of an incident polariton plane wave with a cylindrical wave produced by the scattering on the defect. In momentum space, polariton scattering gives rise to the well-known Rayleigh ring23 that is observed in the far-field images (Figs 2c-IV,3b-IV).

Figure 2: Superfluid regime.
figure 2

(See Supplementary Videos S1 and S3.) Observation of polariton fluids created with a low in-plane momentum of −0.337 μm−1 (excitation angle of 2.6 ∘) and an excitation-laser blue-detuning of 0.10 meV with respect to the low-density polariton dispersion (point A in Fig. 1b). a, Experimentally observed (solid points) and calculated (open points) transmitted intensity (proportional to the mean polariton density) as a function of the excitation power. b, Relative scattered polariton intensity as a function of excitation density, as calculated (open points) and measured experimentally (solid points), in an area in momentum space indicated by the yellow rectangle in c-IV, which drops by a factor of four at the onset of the superfluid regime (red line). c-I–III (c-IV–VI), The experimental near-field (far-field, that is, momentum-space) images of the excitation spot around a defect for the excitation densities marked in a by coloured rectangles. At low power (c-I) the polariton fluid scatters on the defect, giving rise to parabolic wavefronts and a corresponding elastic scattering ring (c-IV). At high powers the emission patterns are significantly affected by polariton–polariton interactions (c-II) and eventually show the onset of a superfluid regime (c-III). In momentum space, the approach and eventual onset of a superfluid regime is demonstrated by the shrinkage (c-V) and collapse (c-VI) of the scattering ring. d, The corresponding calculated images. Solid dot in c-IV and d-IV: momentum coordinates of the excitation beam.

Full size image
Figure 3: Čerenkov regime.
figure 3

(See Supplementary Videos S2 and S4.) Observation of a polariton fluid created with kp=−0.521 μm−1 (angle of incidence of 4.0∘) and an excitation-laser blue-detuning of 0.11 meV with respect to the low-density polariton dispersion (point B in Fig. 1b). a, Experimentally observed (solid points) and calculated (open points) mean polariton density as a function of the excitation power. b-I–III (b-IV–VI), The experimental near-field (far-field, that is, momentum-space) images of the excitation spot around a photonic defect, for the corresponding excitation densities marked in a by coloured squares. At low power the emission is characterized by parabolic wavefronts around the defect in real space (b-I) and by a Rayleigh elastic scattering ring in momentum space (b-IV). As the excitation density is increased, the onset of polariton–polariton interactions leads the system to the Čerenkov regime (cs<vp), characterized by linear wavefronts in real space around the defect (b-II) and a strong modification of the scattering ring in momentum space (b-V). At higher excitation densities the Čerenkov-like regime is maintained (b-III, b-VI). c, The corresponding calculated images. Solid dot in b-IV and c-IV: momentum coordinates of the excitation beam.

Full size image

As the laser intensity is augmented, polariton–polariton interactions increase, resulting in the single-polariton dispersion curves being shifted towards higher energies (blue-shift due to the repulsive interactions) and also becoming strongly distorted as a consequence of collective many-body effects12,13. In a simplified picture, for a specific density |ψc|2, from parabolic (Fig. 1c) the dispersion is predicted to become linear in some k-vector range with a discontinuity of its slope in the vicinity of the pump wavevector kp (see Fig. 1d and refs. 12, 13). Under these conditions, a sound velocity can be attributed to the polariton fluid, being given by

where g is the polariton–polariton coupling strength and m is the effective mass of the lower polariton branch. If the flow velocity vp of the polariton fluid (given by vp=ℏkp/m) is chosen such that the sound speed cs>vp, then the Landau criterion for superfluidity is satisfied, as shown in ref. 13. In such a case, as no states are any longer available for scattering at the frequency of the driving polariton field (see Fig. 1d), the polariton scattering from the defect is inhibited and the fluid is able to flow unperturbed.

This situation is observed in Fig. 2, where the real- (c-III) and momentum- (c-VI) space images of the polariton fluid in the presence of a ∼4-μm-diameter defect are shown for a pump angle of incidence of 2.6∘, corresponding to a low in-plane momentum of k∥=−0.337 μm−1 (vp=6.4×105 m s−1, point A in Fig. 1b). The superfluid regime is first attained only in the centre of the Gaussian excitation spot for the excitation density corresponding to Fig. 2c-II. As the intensity of the excitation laser is increased, the superfluid condition extends to the rest of the spot (Fig. 2c-III), whereas the density in its central part hardly changes. Simulations based on the solution of polariton non-equilibrium Gross–Pitaevskii equations (see ref. 13 and the Methods section) are shown in Fig. 2d. The calculations have been carried out by fitting the size and depth of the defect and by adjusting the values of g and |ψ|2 around the experimentally estimated values (|ψ|2 is obtained from the experimental emitted intensity and g is estimated from the aperture of the Čerenkov fringes as discussed later on). Whereas at low excitation density (Fig. 2c-I,IV,d-I,IV) the fluid presents parabolic density wavefronts in real space and a scattering ring in momentum space as mentioned above, at higher excitation density the scattering ring collapses (Fig. 2c-V,VI,d-V,VI), showing that any scattering of the polariton fluid by the defect is inhibited and that unperturbed flow is eventually attained. In real space (Fig. 2c-III,d-III), a complete suppression of the density modulation is observed (see also Supplementary Video S1). In all these figures, we can see an excellent agreement between the observed effects and the theory.

The collapse of the scattering ring in the superfluid regime is clearly summarized in Fig. 2b, where the ratio between the polaritons scattered to a constant area in momentum space (dashed yellow rectangle in Fig. 2c-IV) and the total polariton density is plotted as a function of the excitation density: when the superfluid regime is obtained, the scattered light drops by a factor of four. Note that this factor is limited here by the finite size of the excitation spot and is expected to attain much higher values if larger pump spots are used.

It is important to stress that the evidence of superfluidity presented here is substantially different from what was observed in ref. 11, which shows the dispersionless propagation of a polariton bullet even when crossing a defect. Although these results strongly suggest a superfluid character, the propagation of the sizeable polariton bullet on top of a homogeneous fluid under parametric scattering conditions cannot be described in terms of the Bogoliubov theory of a weakly perturbed fluid. In contrast, the experimental study reported in the present Letter is consistent with the Landau criterion and allows a clear demonstration of superfluidity in a quasi-homogeneous polariton fluid. It has also been suggested to exploit the Landau criterion to investigate photonic superfluidity in nonlinear optical systems24,25,26, but no experimental studies have yet been reported.

The qualitative shape of the perturbation created in the fluid by the defect is studied in Fig. 3 in a different regime (see also Supplementary Video S2). For this purpose, a polariton fluid with a higher momentum is created using a laser beam with a larger incidence angle, of 4.0∘ (kp=−0.521 μm−1, point B in Fig. 1b). This allows us to enter a regime where the Bogoliubov dispersion of collective excitations has a sound-like nature, with a sound speed that is now lower than the flow speed (cs<vp). This is shown in Fig. 1f, where the calculated spectrum of excitations for the density at which a sound velocity is well defined presents a linearized dispersion together with available states at the same and lower energies than the pump. The generalized Landau condition for superfluidity is not fulfilled and the defect is able to generate collective Bogoliubov excitations in the fluid. They manifest as a Čerenkov-like density modulation pattern with characteristic straight wavefronts in the real-space images (Fig. 3b-II,III) and as a strongly reshaped Rayleigh scattering ring in the far-field emission pattern12,13 (Fig. 3b-V,VI). A similar density pattern was recently observed in atomic Bose–Einstein condensates propagating against a localized optical potential at supersonic velocities27. At lower pump power (Fig. 3b-I,IV), the Bogoliubov excitations go back to single-particle ones (Fig. 1e) and the parabolic-shaped modulation corresponding to the standard Rayleigh scattering ring is recovered, as in Fig. 2c-I,IV. The calculated images also reproduce these observations as shown in Fig. 3c: again, the agreement with the experimental observations is excellent.

Let us note that the observation of the linear Čerenkov-like wavefronts in Fig. 3c-II is a direct indication of the existence of a well-defined sound speed in the system. The measure of the angle of aperture φ between the linear waves generated by the defect allows the precise determination of the sound speed in the system, given by sin(φ)=cs/vp. In the conditions of Fig. 3c-II we find cs=8.1×105 m s−1. With the use of equation (1) the polariton–polariton coupling constant ℏg can be estimated, being of the order of 0.01 meV μm2, which is consistent with previously predicted values on the exciton–exciton interaction28.

We have reported a direct experimental demonstration of superfluidity in a fluid of exciton–polaritons flowing in a semiconductor microcavity. By varying the pump intensity, we have observed that the system goes from a non-superfluid regime in which a static defect creates a substantial perturbation in the moving fluid to a superfluid one, in which the polariton flow is no longer affected by the defect. In a supersonic regime, superfluid propagation is replaced by the appearance of a Čerenkov-like perturbation produced by the defect, in agreement with theoretical predictions and detailed calculations. Our observations pave the way towards the investigation of a rich variety of quantum fluid effects associated with the non-equilibrium nature of the microcavity polariton system.

Methods

Sample.

The sample used in this experiment is an AlGaAs microcavity grown by molecular beam epitaxy. The length of the cavity is 2λ and it contains three In0.04Ga0.96As quantum wells of 80 Å placed at the maxima of the electromagnetic field of the cavity mode. The two Bragg mirrors forming the cavity are made of alternated λ/4 layers of AlAs and GaAs, with reflectivities between 99.85 and 99.95%. In the strong-coupling regime, we measured a Rabi splitting of 5.1 meV. The high finesse of this microcavity leads to polariton linewidths of ∼100 μeV at low power excitation. In the cavity under study the substrate has been polished to make transmission measurements. All discussed experiments have been done at a cavity–exciton detuning of −1.1 meV.

Experimental set-up.

To pump polaritons in our microcavity, we use a frequency-stabilized, continuous-wave, single-mode Ti:sapphire laser (linewidth: 1 MHz). The narrow linewidth and stability of the excitation source is a key parameter in our experiment as it allows the excitation of a well-defined polariton mode.

The beam is spatially filtered by coupling to an optical fibre, it is circularly polarized using zero-order half- and quarter-wave plates and it is focalized on the sample by a lens. To avoid thermal effects caused by the laser illumination, the beam is chopped with a 3.2% duty cycle, at a frequency of about 200 Hz. The light emitted by the microcavity is collected in transmission geometry with a wide-numerical-aperture ocular. The polarization-resolved detection line allows us to simultaneously image the near field (image of the sample) and the far field (the Fourier plane of the collecting ocular, momentum space of the emission). In the latter case, the use of an imaging spectrometer in the detection path allows for the energy–momentum resolution of the emission, giving access to the dispersion curves, such as that shown in Fig. 1b.

Gross–Pitaevskii equation.

Figures 2d and 3c show the result of simulations based on the solution of the polariton non-equilibrium Gross–Pitaevskii equations:

where

ψX(C) is the exciton (cavity-photon) wavefunction, x the in-plane two-dimensional space vector, t time, Fp, ℏkp and ℏωp the amplitude, momentum and energy of the pump field, respectively, ℏωX(C) the energy of the excitons (cavity photons) at k=0, γX(C) the decay rate of the excitons (cavity photons), 2ΩR the vacuum Rabi splitting between the polariton modes, VX(C) the excitonic (photonic) potential that accounts for the defects present in the sample and g the exciton–exciton interaction potential. x0 indicates the bidimensional coordinates of the centre of the Gaussian spot on the sample, and δx is the radial width of the circular Gaussian spot. Let us note that in our simulations we have just considered photonic defects with a depth of 1 meV, that is, VX=0, but similar results are expected in the case of considering excitonic defects. In the simulations, the size of the defects is 4 μm and 5 μm, respectively, for Figs 2 and 3.

Only for the calculation of the spectra of excitations presented in Fig. 1, the Gross–Pitaevskii equation was used for a spatially homogenous excitation. In this case, the equations have been linearized around the steady-state solution, allowing us to calculate the Bogoliubov-like excitation spectrum as discussed in refs 12 and 13.

Note: When originally published online, the supplementary information for this article was incomplete. The new complete version is now available to download.