Main

Earlier angle-resolved photoemission spectroscopy (ARPES) experiments mapped the basic band structure of URu2Si2 in the paramagnetic state (above To), establishing the existence of hole pockets at the Γ, Z and X points of the Brillouin zone15,16,17. These experiments revealed strong disagreements with the calculations for the electronic structure and the Fermi surface of URu2Si2. It was speculated that this was due to the presence of narrow features from the U–5f states, not taken into account by the calculations, and difficult to characterize experimentally with the resolutions available at that time17. So far, no reports exist of high-resolution ARPES experiments below or across To. The pressing question is to determine experimentally the electronic structure near the Fermi level (EF), including the heavy 5f states, above and below To.

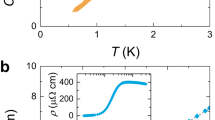
Figure 1 summarizes our findings for the temperature evolution of the electronic structure near EF. Figure 1a shows the spectra of electrons with k∥, the momentum component parallel to the sample surface, integrated over angles along the (110) direction at two temperatures above and below To. At T=26 K, that is, above To, the only apparent feature is a surface state at binding energies EB<−35 meV, observed at all investigated temperatures (see Supplementary Information). In contrast, at 13 K, below To, a narrow peak at EB≈−7 meV appears, indicating the presence of a quasiparticle band. A systematic study of the temperature dependence of this quasiparticle band is shown in Fig. 1b–d. In these figures, we normalized the spectra by the Fermi–Dirac distribution, following a well-established procedure18 to reveal the thermally occupied part of the spectral function up to energies ∼5kBT above EF. The angle-integrated data of Fig. 1b show that at 26 K the quasiparticle band lies at EB≈5 meV; at 18 K≈To it appears right at EF, and below To the band shifts to energies below EF. At 10 K, the quasiparticle peak is located at EB≈−7 meV. Figure 1c presents a quantitative evaluation of the integrated quasiparticle band energy as a function of T/To from several spectra taken along the (110) and (100) directions, implying that the shift of this quasiparticle band occurs over an extended region of momentum space. Figure 1d shows the angle-resolved data at the same temperatures as in Fig. 1b. The data at 26 and 18 K show a flat band above EF and at EF, respectively. It corresponds to the narrow peak observed in the angle-integrated data of Fig. 1b at those temperatures. Interestingly, the spectral weight of this flat band seems to be confined to a momentum region within k∥=±0.2 Å−1, momenta at which there is a clear hint of a Fermi-level crossing. In the spectra at 13 and 10 K, that is, below To, the quasiparticle band exhibits a narrow dispersion, showing that it is a band of itinerant heavy quasiparticles. We will discuss all of these observations in detail below.

Figure 1: Temperature dependence of the heavy-quasiparticle band in URu2Si2.
figure 1

a, Photoemission spectra integrated within ±0.2 Å−1 along the (110) direction at 13 K (blue) and 26 K (red). Below To=17.5 K, a quasiparticle (QP) peak appears below EF. For all temperatures, a surface state (SS) at EB<−35 meV is observed. b, Spectra integrated within ±0.2 Å−1 along the (110) direction and normalized by the Fermi–Dirac distribution, at various temperatures around To: 26 K (red), 18 K (green), 13 K (blue) and 10 K (black). The zero-intensity level of each spectrum is indicated by the colour bars in the right axis. The triangle markers give the peak position. c, Energy of the quasiparticle peak in the integrated spectra as a function of T/To for cuts along the (110) (triangles) and (100) (circles) directions. The error bars in T are due to thermal instabilities during the experiment. The error bars in the peak energy are calculated from the peak positions in spectra integrated over different momenta windows around k∥=0. d, Angle-resolved spectra along the (110) direction for the same temperatures as in b. The intense hole-like feature dispersing below EB∼−35 meV is the surface state shown in a.

Full size image

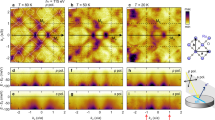
Figure 2 shows the angle-resolved data along the (110) direction at T=13 K. The ARPES intensity map (Fig. 2a) shows the narrow quasiparticle band dispersing down to W≈−7 meV, where |W| is the width of the band. Figure 2b shows energy distribution curves (EDCs) in the region close to EF of this intensity map. The EDCs having the leading edge closest to EF are plotted in bold, corresponding to momenta kLE=±0.2 Å−1. For |k|<|kLE|, distinct quasiparticle peaks of resolution-limited width (∼5 meV) are observed. From the values of W and kLE, an estimate of the effective mass () of these quasiparticles can be obtained from the relation . This yields (me is the free electron mass), confirming that this band corresponds to heavy quasiparticles. This value of is among the largest values ever measured by ARPES in any material. The values of and kLE agree well with values given by specific-heat data6 and de Haas–van Alphen measurements7. Notice also from Fig. 2b that for |k|>|kLE| the leading edge of the spectra shifts to larger binding energies. This suggests that the spectral weight of the heavy-quasiparticle band spreads over a large momentum window, as best seen in data along the (100) direction (see Fig. 3). Figure 2c shows momentum distribution curves (MDCs) from the intensity map in Fig. 2a. Besides the peaks corresponding to the hole-like surface state, two lateral shoulders are observed (shown by the dashed lines). They correspond to a light-hole-like conduction band with , dispersing through EF at Fermi momenta kF=±0.2 Å−1, that is, kF=kLE within experimental resolution. Figure 2d shows the average of the energy and momentum second derivatives of the intensity map in Fig. 2a. This enables us to visualize the conduction band and the spectral weight of the heavy-quasiparticle band spreading beyond |kLE|.

Figure 2: Heavy-quasiparticle band in the hidden-order state and hybridization with a conduction band along the (110) direction.
figure 2

a, ARPES intensity map along the (110) direction at 13 K. The map shows a heavy-quasiparticle band dispersing down to ∼7 meV below EF. b, EDCs of the intensity map in a in the region close to EF. The EDCs in which the leading edge is closest to EF are drawn in bold. c, MDCs from the intensity map in a. Each MDC is normalized to its area. The two central peaks correspond to the hole-like surface state, and two lateral shoulders to a light conduction band that disperses through EF. d, Average of second derivatives along the energy and momentum axes (see the Methods section), showing the heavy-quasiparticle band, the surface state and the hole-like conduction band. In all panels, the dashed lines are guides to the eye.

Full size image
Figure 3: Heavy-quasiparticle band in the hidden-order state and hybridization with a conduction band along the (100) direction.
figure 3

a, ARPES intensity map along the (100) direction at 15 K, with the heavy-quasiparticle band dispersing down to ∼4 meV below EF. The dotted white lines show conduction bands dispersing through EF. b, EDCs of the intensity map in a in the region close to EF. The EDCs in which the leading edge is closest to EF are drawn in bold. The dashed line is a guide to the eye for the dispersion of the heavy-quasiparticle band. This band, clearly extending beyond the Fermi momenta, is also visible in the raw data map of a.

Full size image

Figure 3 summarizes the data along the (100) direction at T<To. The raw map (Fig. 3a) clearly shows the band of itinerant heavy quasiparticles approaching EF at kLE=±0.15 Å−1, the light-hole-like conduction band dispersing through EF at the same momenta and the tails of spectral weight extending beyond |kLE|. The last of these have a clear quasiparticle peak structure, as seen in the corresponding EDCs (Fig. 3b), with a hole-like dispersion of velocity ∼12 meV Å, estimated from the peak’s change in energy in the momentum range [−0.15,−0.6] Å−1.

We now discuss the implications of our data, and the links to observations from other probes. Our results explicitly demonstrate that itinerant heavy quasiparticles participate in the Fermi-surface instability that leads to the hidden order in URu2Si2, as indirectly suggested by recent neutron-scattering and transport experiments9,10. Furthermore, note from Figs 2 and 3, that the momenta where the conduction band and heavy quasiparticle coincide correspond to the momenta where the heavy-quasiparticle band bends back from EF. This suggests that the whole structure arises from the hybridization of the light conduction band with a band of localized states, probably of 5f character; however, owing to the finite experimental resolution, we cannot observe a hybridization gap directly. From our angle-resolved data at 26 and 18 K in Fig. 1d, it seems that these bands hybridize already above To, when the band of localized states is at EB>EF. This agrees with the observed rapid drop in resistivity below ∼50 K in URu2Si2, which is usually ascribed to the crossover from the single-impurity to the coherent quasiparticle behaviour6. Indeed, previous ARPES experiments on URu2Si2 above To showed strong evidence for the presence of f–d hybridization17. The transition to the hidden-order state shifts the heavy-quasiparticle part of the resulting spectral function to EB<EF. There, it is clearly observed as a dispersing band of heavy quasiparticles, creating a new heavy-electron pocket embedded within the light-hole pocket already present at T>To. The Fermi momenta of the heavy-electron and light-hole pockets are very close (indistinguishable with our resolution), implying compensated Fermi-surface volumes. This explicitly confirms recent conclusions based on the observed quadratic field dependence of the magneto-resistance at T<To (ref. 19). Moreover, such a band-shift across the Fermi surface might be the microscopic origin of the observed changes in the thermal and transport properties of URu2Si2 during the hidden-order transition4,6,8,9,11. For instance, from the resolution-limited width of the heavy-quasiparticle peak, a lower limit for the heavy-quasiparticle lifetime can be estimated, yielding 0.13 ps. The group velocity of these quasiparticles (see Fig. 2) is |vQP|≈|W/kLE|=35 meV Å. Thus, our data can explain thermal transport measurements9,20 that found that heavy electrons of comparable Fermi velocity, and with lifetimes of about  ps, appear below To: such long-lived heavy electrons arise from the heavy-quasiparticle band dropping below EF. Note also from Figs 2 and 3 that the Fermi wavevectors along the (100) and (110) directions are small and different, proving the existence of anisotropic small-sized Fermi-surface pockets around the Γ point in URu2Si2, as indirectly suggested by other techniques7. As pointed out recently19, the existence of an anisotropic Fermi surface with multi-band compensated structure, directly observed in our data, is of prime importance in understanding the exotic superconducting state of this material (Tc=1.5 K) for which the hidden order is a precursor.

The reordering of the portions of the Fermi surface that involve heavy quasiparticles, shown by our data, is not predicted by any current theory of the hidden-order transition, including recent state-of-the-art density-functional calculations of the electronic structure21. Furthermore, such a kind of Fermi surface instability, which in the case of the hidden order is associated with a second-order phase transition and the onset of a collective order of yet unknown nature, has never been observed before. It differs, for instance, from the single-impurity to coherent-Kondo-lattice transition, in which the f-electrons, although shifted by the hybridization with the conduction band, become incorporated to the Fermi surface only after the transition, the transition not being of second order. It also differs from usual density-wave transitions, which induce only back-folding of the participating bands. In fact, several theories and recently proposed scenarios suggest that the hidden-order arises from some kind of Fermi-surface nesting22,23,24,25. Although this is an interesting possibility, we note that our results cannot be understood in terms of band-nesting alone, putting strong constraints on models for the hidden-order transition.

One way of interpreting our data is that the hidden-order transition reorganizes the spectral function of this strongly interacting many-electron system. The observed shift of the heavy-quasiparticle band would then be a consequence of this many-body effect. A proof-of-principle of this possibility, which does not need to invoke band-nesting, has been recently given for the specific case of the magnetic order–disorder transition in the two-dimensional doped Kondo-lattice model26, but the underlying model is general to any collective mode (not necessarily of magnetic origin). In this scenario, the reconstruction of the heavy-fermion Fermi surface would be driven by a collective mode that is in competition with, and has the same energy scale as, the Kondo screening. In the case of URu2Si2, where it is established that the transition is not of magnetic origin27, the field is open for material-specific theoretical investigations to test this idea.

We anticipate that our results will be an invigorating trigger in the experimental and theoretical exploration of the fascinating behaviour of URu2Si2 and the hidden-order puzzle. Future experiments should address the important questions of the precise shape of the Fermi-surface topology, including the heavy-quasiparticle pockets, and how other portions of it change, or get gapped, across the transition. High-resolution soft-X-ray resonant photoemission experiments28 could be used to test whether the heavy band around the Γ point is of 5f character. Future theories should incorporate heavy fermions, possibly through d–f hybridization, together with strong correlations, something not done yet for URu2Si2, to explore how collective modes would lead to the kind of instability observed here.

Methods

Sample preparation and measurement technique.

The high-quality URu2Si2 single crystals were grown in a tri-arc furnace equipped with a Czochralski puller, and subsequently annealed at 900 ∘C under ultrahigh vacuum for 10 days29. The high-resolution ARPES experiments were carried out with a Gammadata R4000 analyser and a monochromatized vacuum ultraviolet lamp at h ν=21.2 eV (He Iα). At this photon energy, the accessed region in momentum space at near-normal emission is very near the Γ point (less than 0.15 Å−1 above Γ002; ref. 17). The energy resolution for the used analyser settings was 5.18 meV, determined similar to previous experiments30. The temperature during each measurement was found by fitting a Fermi–Dirac distribution to the Fermi edge of polycrystalline Ag, mounted next to each URu2Si2 crystal on the same sample holder, and taking into account the above energy resolution. The base pressure in the chamber was 1×10−10 mbar, increasing to 8×10−10 mbar during the measurement owing to the He leakage from the discharge lamp. The crystals were oriented using Laue diffraction, and cleaved in situ already at the measurement temperature, exposing the (001) surface. Highly ordered surfaces were confirmed by sharp low-energy electron diffraction patterns measured on each sample after the measurements.

As a result of the observed high-surface reactivity (the quasiparticle peaks below To broaden and lose amplitude within 2 h after cleavage), each data set at a fixed temperature in Figs 1–3 was obtained on a new, freshly cleaved surface, and the duration of each measurement was kept below 15 min immediately after cleaving. The changes with temperature of the spectra were checked and reproduced on single cleaves (the data, of lower quality, are not shown).

Procedure of second-derivative rendering.

The raw photoemission intensity maps were convoluted with a two-dimensional Gaussian of widths σE=7 meV and σk=0.07 Å−1. Second derivatives along the EB and k∥ axes were normalized to the maximum intensity of the surface-state peak, then averaged. Only negative intensity values, which represent peak maxima in the original data, are shown.