Main

Synthesis of single-crystal NaxCoO2·yH2O is difficult, and polycrystalline samples often show inhomogeneities in Na distribution and H2O accumulation15,16. Once synthesized, the compound is chemically unstable at ambient temperature and humidity17, making it problematic to handle and characterize. Thus, well-reproducible and reliable experimental results that could be expected to unravel details about the precise superconducting state have been slow to emerge. Still, several experimental facts that are rather well established and reproducible bear immediate relevance to the superconducting symmetry. Other specifics that follow from confirmed knowledge about the crystal and electronic structure allow the exclusion of at least a few of the symmetry-allowed pairing states.

In Table 1, we list all the different symmetry representations that are compatible with a hexagonal crystal structure up to orbital angular momentum L=3 (that is, up to the f-states), according to ref. 14. The first 25 are even frequency states and the last is an isotropic odd-frequency state, to be discussed later. Some of these states can be excluded from consideration on the basis of their non-conformity with what is known about the physical and electronic structure of NaxCoO2·yH2O (criterion 1), whereas some others can be eliminated on the basis of the the non-observance of characteristic effects associated with them (criteria 2 and 3). Remarkably few candidates survive all three criteria and each candidate turns out to be highly unconventional. Below, we list our criteria, the established facts they are based on and the consequences for the pairing states.

Table 1 A list of all symmetry-allowed pairing states for the hexagonal symmetry. The orbital angular momentum, L, of each state is labelled in the rightmost column and conformity/non-conformity with each of our three criteria is indicated by Y/N (for yes/no) in the remaining three columns.
Full size table

(1) Two-dimensionality. Electronic structure calculations for the hydrated compound show an anisotropy in the Fermi velocity of at least an order of magnitude, which is supported by an experimentally measured18,19 resistance anisotropy of 103–104. The corresponding Fermi velocity anisotropy is 30–100, indicating that transport along the c axis is probably incoherent. This is firm evidence that the electronic structure is very strongly two-dimensional. As found experimentally20,21 and explained theoretically22, the magnetic anisotropy of the unhydrated high-Na-content compounds is very small, primarily because each Co couples with seven Co atoms in neighbouring layers. Although there are no data on the magnetic coupling at x=0.3, or for the hydrated compound, the reduction in magnetic coupling can be estimated from the ratio of the squared Fermi velocities, which is ∼20. Thus, in the hydrated compound, magnetic interaction is also expected to be two-dimensional. Furthermore, in contrast to phonons in the cuprates, the Co and O phonons in NaxCoO2·yH2O should be two-dimensional. Of course, vibrations involving the intercalated water need not be two-dimensional, but the absence of a hydrogen isotope effect18 clearly indicates that these are irrelevant for the superconducting pairing.

Therefore, we conclude that the superconducting order parameter in NaxCoO2·yH2O should be two-dimensional.

(2) Absence of a finite superconducting gap. The temperature dependence of the density of states (DOS) gives information about the structure of the superconducting gap. DOS probes for NaxCoO2·yH2O have measured the temperature dependence of either specific heat23,24 or relaxation rates (nuclear magnetic resonance5, nuclear quadrupole resonance25,26 and muon spin relaxation, μSR3,27). In all of these works, the authors agree that the low-temperature behaviour of the DOS is not exponential, indicating the absence of a full gap. As of yet, no group has reported specific heat measurements at temperatures T low enough to allow for certain determination of the exact temperature dependence, but most authors suggest a T2 (line nodes) behaviour for T≳2 K and linear (finite DOS) behaviour at lower T. However, one should keep in mind that anisotropic gaps of very different magnitudes on the two Fermi surfaces (see below) could emulate line node behaviour, although not at very low temperatures.

These results exclude states with a fully developed sizeable gap on all Fermi surfaces.

(3) Absence of superconductivity-induced spontaneous magnetic moments below the critical temperature Tc. Some of the superconducting states listed in Table 1 (9, 12) are non-unitary and have a spontaneous magnetization in the superconducting state. Others (6, 18, 21) break the time-reversal symmetry of a Cooper pair by virtue of a non-zero pair orbital moment. In both cases, the resulting non-zero local magnetic moments should be detectable14. Domain formation and internal Meissner screening prevent the development of net magnetization in the latter case, but crystallographic defects and grain or domain boundaries should still host detectable non-zero local moments. The accepted interpretation of the appearance of disordered static magnetic moments below Tc is that the Cooper pairs carry a non-zero orbital moment. In all reported μSR experiments3,28 for NaxCoO2·yH2O, there is no indication of static moments below Tc. As the μSR signal is determined by the fraction of muons that are stopped in a part of the crystal containing sufficient static magnetic moments to cause detectable precession, these experiments are part of a rare class in which poor sample quality makes the effect more pronounced rather than obscuring it. It would be impossible to calculate the probability of detecting muon precession from first principles. We can, however, make a meaningful comparison with another layered compound, Sr2RuO4, in which there is confirmed μSR detection of static magnetic moments29. NaxCoO2·yH2O must have a significantly higher volume concentration of Cooper pairs (based on its three times higher Tc, the gap is presumably larger), each Cooper pair has an orbital moment of the same or greater magnitude and there is a much higher defect concentration. The volume fraction of NaxCoO2·yH2O containing a static magnetic field detectable by μSR should therefore be greater (perhaps by an order of magnitude) than in Sr2RuO4, ensuring that the non-observance of muon precession indeed indicates the absence of an orbital moment on the Cooper pairs. Non-unitary states would have a defect-independent magnetization of the order of d*×d/|d|2∼1 μB (where μB is the Bohr magneton and d is the vector order parameter) per pair, and should be even more detectable.

Therefore, we conclude that non-unitary states, or those with an unquenched orbital moment, are not possible in NaxCoO2·yH2O.

We now examine the 25 symmetry-allowed even frequency states listed in Table 1 for their agreement with the aforementioned three criteria. In accordance with two-dimensionality, we eliminate the ten states that have, by symmetry, strong z-dependence of the order parameter. Of the remaining 15 states, seven have no symmetry restriction that would require them to have node lines or points. In general, there exists the possibility of accidental rather than symmetry-induced nodes or regions with a finite but extremely small order parameter. Given the specific fermiology (see Fig. 1) and six-fold symmetry of NaxCoO2·yH2O, the order parameter would have to vary on the order of 0.2–0.25 of the Brillouin zone dimension to generate such accidental nodes, making this situation highly unlikely. The μSR experiment allows us to exclude five more states that are non-unitary or have a pair orbital moment (several of these were previously excluded as having a full gap).

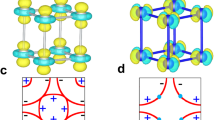
Figure 1: The two predicted Fermi surfaces of Na0.3CoO2·yH2O shown inside the conventional Brillouin zone.
figure 1

The two f-wave pairing states that remain after eliminating any states that are in conflict with experimental evidence are superimposed. a, The state has node lines (dashed) that directly intersect the theoretically predicted small hole pockets. b, The node lines of the state fall between the small pockets and therefore cause no loss of pairing energy.

Full size image

This leaves six remaining states: 4, 5, 16, 17, 22 and 23. There is good reason to believe that the first four are not realized. As an example, we consider the first pair and . In the linear approximation, they are degenerate with each other and with state 6, (see ref. 14). Strong coupling effects, the spin–orbit interaction and other effects can, formally, tilt the energy balance in favour of these states, but only in the fourth order in the order parameter. All three states belong to the same symmetry representation, but the first two have node lines in the energy gap, whereas has a full gap everywhere. This leads to a considerable loss of pairing energy compared with the fully gapped state and makes stabilization of other states in the same representation unlikely.

Excluding states 4, 5, 16 and 17 on the basis of the previous argument, there remain only two possible states: and . We can make no further distinction between the two if we assume that only the large observed30 Fermi surface around the Γ point exists. However, band-structure calculations predict six smaller Fermi surfaces that carry 2/3 of all electrons at the Fermi level. In the state, there are line nodes between each of these surfaces, whereas in the state the line nodes intersect them (see Fig. 1). Given the small surface size, the line node would cause a near total loss of pairing for 2/3 of the electrons in the latter state. Therefore, we conclude that if the small Fermi surface pockets exist, the most probable superconducting symmetry among all possible states with an even-frequency order parameter is the f state .

The analysis above applies to superconducting ordering with an order parameter that depends on frequency as Δ(−ω)=Δ(ω), as in the Bardeen–Cooper–Schrieffer theory. In principle, symmetry allows for an odd-frequency dependence, Δ(−ω)=−Δ(ω). There is a full set of odd-frequency states that also conform to the hexagonal symmetry. We don’t discuss explicitly all but the isotropic case, because the odd-frequency class of states is intrinsically gapless and therefore has a lower pairing energy even for s-wave symmetry. Anisotropic states are even further suppressed energetically and are probably not realistic candidates. The odd-frequency triplet state (26 in Table 1), proposed by us in ref. 13, is fully compatible with all three criteria introduced above. It is without orbital moment, unitary and two-dimensional. Despite being isotropic, it has a finite DOS at zero energy, in accordance with the observed non-exponential behaviour of DOS-sensitive quantities. The ground state in this case is defined either by the spin–orbit-induced anisotropy of the pairing interaction or by the spin–orbit-induced magnetic anisotropy, which favours a state when the easy magnetization axis is out of the plane and a or state when it is in the plane.

Finally, we would like to comment on the (still controversial) Knight shift experiments2,3,4,5. The f-wave states that have emerged from our discussion correspond to Cooper pairs with spins in the xy plane and thus to a constant Knight shift. The same is true for the state. On the other hand, or would show a reduced, although not exponentially reduced, Knight shift below Tc. Of the states with an even frequency gap (1–25), there are six (4, 5, 6, 15, 22 and 23) that, formally, should not show a reduction of the in-plane Knight shift reduction below Tc.

The superconducting state of NaxCoO2·yH2O cannot be conclusively stated, but the number of viable candidates can be reduced to a manageable number through careful comparison of reliable data and allowed symmetries. The results of our deductive process are surprising, but we hope that focusing attention on these few highly unconventional states will accelerate progress towards resolving the exact pairing symmetry. In the words of an earlier investigator, “It is an old maxim of mine that when you have excluded the impossible, whatever remains, however improbable, must be the truth” (Sir Arthur Conan Doyle, The Adventures of Sherlock Holmes).