Main

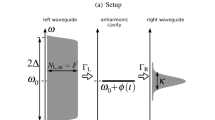
We investigate an optical analogue of the superconducting Josephson interferometer, which we name the quantum-optical Josephson interferometer, revealing new features due to the genuine non-equilibrium interplay of coherent tunnelling and on-site interactions. We consider two variants of the proposed device with a central nonlinear cavity coupled to two external driving lasers through either two side cavities (Fig. 1a,b) or two waveguides (Fig. 1d). The three-cavity system can be generalized to an N-cavity system with a central nonlinear one14 (Fig. 1c), and in the limiting case of very large N this reduces to the single cavity coupled to two side waveguides (Fig. 1d). In both cases, the coupling to the side cavities (or waveguides) is a consequence of photon tunnelling. We assume the central cavity to have a sizable single-photon nonlinearity, for example due to some radiation–matter interaction, be it Jaynes–Cummings-type interaction (with a single atom or quantum dot in the central cavity)15, giant Kerr nonlinearity1 or confined polariton interaction (for example with a quantum well embedded in the cavity)16. The model discussed here is fairly general and can be realized in a variety of quantum-optical systems. In the following we show that the light emitted from the central cavity reflects the interplay of two competing effects, tunnelling and interactions. As the relative magnitude of the interaction parameter is varied with respect to the tunnelling strength, the system shows a crossover between a coherent and a strongly correlated regime. In the coherent regime, photons are delocalized over the three cavities and the emitted light strongly depends on the phase difference between the two pumping lasers (Josephson oscillations). In the strongly correlated regime instead, the inhibition of photon number occupation beyond Fock states |0〉 and |1〉 in the central cavity reduces the quantum coherence between the two outer ones. The suppression of Josephson oscillations in the emitted light is accompanied by a crossover from Poissonian to sub-Poissonian photon statistics.

Figure 1: The systems under consideration.
figure 1

a, Schematic diagram of the quantum-optical Josephson interferometer with three coupled cavities. The relevant quantities of the model are defined in the text. b, A possible photonic-crystal-based implementation (with calculated cavity mode profiles), where the middle cavity can contain a quantum dot or a quantum well in strong coupling with the high-quality-factor photonic crystal cavity mode. c, Schematic diagram of an interferometer in the limit of a large number of coupled linear cavities in optical contact with the central nonlinear cavity, in which only the edges of the system are pumped. d, A possible solid-state implementation of c, using a photonic crystal circuit with two side waveguides coupled to the central nonlinear cavity.

Full size image

Photon correlation measurements reveal features of an interacting few-body system that are not captured by more traditional transport-type measurements. In fact, the device we propose has close analogies with a phase-biased Cooper pair transistor. In the latter, the critical current can be electrostatically modulated by changing the gate potential on the central island connected to two superconducting reservoirs17,18. The interplay between coherent tunnel coupling and on-site interactions in these systems has been used in many ground-breaking experiments, ranging from the observation of a quantum phase transition in Josephson junction arrays19 to the direct demonstration of number–phase uncertainty in superconducting islands20. Although the operation of both electronic and photonic versions is based on the quantum-mechanical conjugation between phase and number variables, the quantum-optical Josephson interferometer is an intrinsically open system. Given the enormous impact of the Josephson devices in electronics, from metrology to quantum information processing, we expect that the quantum-optical Josephson interferometer might constitute the building block for a new class of quantum-optical devices.

In the absence of losses the three-cavity set-up depicted in Fig. 1a,b is described by the Hamiltonian

written in the rotating frame with respect to the frequencies of the two pumping lasers (ℏ=1). In the above equation, Δk=ωk−ωL are the detunings of the coherent pump lasers whose amplitudes are E1,3=|E1,3|exp{i φ1,3}, where |E1,3| are assumed to be time independent (cw pumping). We will characterize the three-cavity system by analysing the response of the central cavity as a function of the phase difference φ=φ3−φ1. The two couplings J and U quantify the hopping strength between neighbouring cavities and the nonlinear photon coupling in the central cavity, respectively. The operators describe non-interacting bosonic fields in the external cavities, that is, free cavity photons, whereas the elementary excitations in the central cavity are interacting polaritons denoted by . Both the tunnelling and the coherent pumping act on purely photonic degrees of freedom; for example, J is due to the overlap of the photonic component among nearest-neighbour cavities. A rigorous derivation of the model in equation (1) inevitably depends on the specific system under consideration and has been provided before in the context of atomic9 or solid-state16 cavity quantum electrodynamics implementations. Readily accessible schemes for achieving large photon–photon interactions are based on resonant coupling of a single emitter to a cavity mode (that is, the Jaynes–Cummings model). As discussed in the Supplementary Information section ‘Experimental feasibility’, the principal features we obtain using model (1) are qualitatively identical to those predicted by the Jaynes–Cummings-type single-photon nonlinearity.

The dynamics of the full model, equation (1), is effectively equivalent to that of two coupled bosonic fields: one is coherently driven, whereas the other is nonlinear (see the Methods section). From now on we consider for simplicity the case of equal detunings and resonant pumping, Δk=Δ=0. Losses can be taken into account within the quantum Master equation in the Born–Markov approximation for the system density matrix ρ, which is expressed in the usual Lindblad form21:

In most of the relevant regimes, the Master equation has to be solved numerically. A description of the approach used in this work is presented in the Methods section. In the remainder of the text, we shall assume γ1,3=γ. With the specific experimental realizations of Fig. 1b,d in mind, typical parameter values are as follows: inter-cavity tunnel coupling J≃1 meV (ref. 22); γ≃0.01 meV (for a cavity with a quality factor of Q≃105 in the optical/near-infrared domain)23. With these values, a ratio of U/γ=10 (see Supplementary Information) can readily be achieved with the currently available technology.

It is instructive to first consider the case of vanishing interaction (U=0), where an exact analytical solution for the steady state of equation (2) can be obtained. The case of equal amplitudes of the two driving lasers (E1=E3=E) and equal losses in the three cavities (γ=γ2) captures all the essential details of the non-interacting case. In the steady state the average number of photons in the central cavity is found to be

This is the analogue of Josephson oscillations, imprinted in the light emitted from the central cavity, due to the interference between the two coherent driving fields. Two features of this solution are to be noticed for a comparison with the more interesting situation treated below. First, the size of the oscillations is maximized at J∼γ/2 as a result of an interplay of dissipation and interference. Second, although 〈n2(φ=0)〉 is suppressed and eventually goes to zero for J≫γ, the oscillations keep a cosine-like behaviour as a function of φ.

In Fig. 2, we present our numerical results for experimentally accessible observables of the system when the interaction is switched on (U>0). Rescaled quantities and are defined for the effective two-cavity model as outlined in the Methods section. Do the Josephson oscillations in 〈n2(φ)〉, as measured by detecting the light emitted from the central cavity (Fig. 1b), remain intact? In Fig. 2a, we plot 〈n2(φ)〉 for various values of the interaction at a pumping strength of . The size as well as the functional form of the oscillations barely changes as is varied across a wide range of values under weak-pumping conditions. This picture changes dramatically when we pump the system more strongly, shown in Fig. 2b for . Here, the average population in the central cavity can be sizeable and nonlinear effects are more pronounced. In contrast to the weak-pumping case (Fig. 2a), the size of the oscillations is suppressed to a great extent as U is increased. Besides the suppression of visibility, Fig. 2b shows a strong deviation from the cosine-like functional form, equation (3), as is increased from zero (the behaviour for is shown in the inset).

Figure 2: Numerical solutions for the three-cavity system.
figure 2

a, Average population in the central cavity as a function of φ for different values of , in the weak-pumping regime (): Josephson oscillations are barely modified as U is increased. b, The same quantity as in a, but for a stronger drive (): Josephson oscillations are suppressed by increasing the interaction strength. The inset shows a magnification of the curve calculated for (compare with Fig. 3b, inset). c, Second-order correlation function as a function of and U for γ/γ2=5 under weak-pumping conditions, , showing the transition from Poissonian (red) to sub-Poissonian (blue) light statistics. The functional dependence is highlighted with a dashed white line.

Full size image

Next we investigate how this crossover is reflected in the photon statistics of light emitted from the central cavity. For this, in Fig. 2c we plot the zero-time-delay second-order correlation function g2(2)(0) (see the Methods section) as a function of the scaled quantities U/γ2 and . We find that g2(2)(0) shows a sharp transition from Poissonian to sub-Poissonian light statistics as the interaction strength U is increased. The threshold for antibunched (sub-Poissonian) light generation, Uth, is a function of J. For the antibunching threshold is , whereas for . These two regimes are connected by a smooth crossover region. This peculiar behaviour of the antibunching threshold is related to the effective dissipation rates of the coupled system as the coupling strength is varied. At small , the coupling to the central cavity is perturbative; the nonlinearity (that is, antibunching) therefore sets in when U is larger than the broadening of the bare central cavity polariton states, that is, γ2. As is increased, the coupling becomes non-perturbative and the relevant eigenstates of the coupled system are superpositions of centre and outer cavity states; such dressed states have broadening contributions from both centre and outer cavities and therefore the nonlinearity now has to be larger than the broadening of the dressed states for the system to show antibunching. A simple expression for g2(2)(0) can be derived in the weak-pumping limit (see the discussion in Supplementary Information), which captures all the regimes discussed:

where Γ=γ+γ2 and . These results are consistent with the expectation that strong photon nonlinearity can lead to photon blockade1 in the central cavity, giving rise to antibunching. Although the relative strength of U with respect to tunnel coupling seems to matter at small couplings (that is, is a monotonic function of ), at larger the relative effect of U saturates. Note that the nature of the nonlinearity of the system does not leave any footprint in the observables we have considered. Indeed, the coupled system maps onto an effective Jaynes–Cummings model, where the tunnel coupling strength plays the role that is commonly played by the atom–cavity dipole coupling in the original Jaynes–Cummings model15 (see Supplementary Information). For , the deviation of the system energy levels from a harmonic structure is linearly proportional to U, and this determines the main behaviour of g2(2)(0).

In the limit , or when an infinite number of linear cavities are coupled on either side to the central cavity (Fig. 1c), we obtain a band of bosonic modes, which mimic two external waveguides. In this case the corresponding photon creation/annihilation operators in equation (1) can be replaced by their average (coherent-state) values, p1,3→〈p1,3〉=−2i E1,3/γ. The effective Hamiltonian of the system reduces to that of a single nonlinear cavity pumped by a coherent field with amplitude Eeff=−2i J(E1+E3)/γ, that is,

We choose parameters such that |Eeff|=J, that is, J acts as the effective pumping rate. The steady-state results for g2(2)(0) and 〈n2〉 are shown in Fig. 3a,b, respectively. We find that g2(2)(0) shows a sharp transition from Poissonian to sub-Poissonian light statistics as the interaction strength U is increased. The threshold for antibunched (sub-Poissonian) light generation, Uth, is a function of J. For J/γ2≪1 the threshold goes as Uth∼γ2; in the opposite limit Uth∼J. As in the previous case at small hoppings, the antibunching sets in when U is larger than the broadening of the bare central cavity polariton states (γ2). Much more interesting is the fact that at larger hoppings the threshold scales with J, in contrast to the case of three cavities (Fig. 2c). The crossover from Poissonian to antibunched behaviour reflects in a clear way the crossover from delocalized to localized states. As J is increased the relevant eigenstates of the coupled system are superpositions of centre and outer cavity states, whereas in the opposite case the good eigenstates are the Fock states due to the onset of photon blockade. We may also understand the dependence of the crossover on J by relating it to the low-J limit of Fig. 2c: from the perspective of the central cavity, the driven waveguide is analogous to a driven cavity with a dissipation rate larger than all other energy scales.

Figure 3: Numerical solutions for the waveguide-coupled limit.
figure 3

We assume the coherent states |〈p1,3〉|=1. a, Second-order correlation function at zero time delay for light emitted from the central cavity, as a function of U and J. A sharp crossover between Poissonian (red) and sub-Poissonian (blue) statistics is seen in the U–J plane. b, Average population in the central cavity for J/γ2=2 as a function of φ, for different values of U/J. The oscillations approach the limiting case of equation (6) when U/J≫1. The inset is a zoom on the curve for U/J=10, showing 〈n2(φ=0)〉→0.5 and a strong deviation from cosine-like behaviour (compare with Fig. 2b, inset). c, g2(2)(0) and 〈n2(φ=0)〉 as a function of U/J for different values of J/γ2, showing a smooth crossover from the delocalized to the localized regime for U/J>1.

Full size image

Owing to the Heisenberg uncertainty relation, the crossover from bunching to antibunching behaviour also manifests itself in the phase dependence of 〈n2〉 shown in Fig. 3b. On increasing the interaction the visibility is strongly suppressed, and furthermore there is a marked deviation from the simple cosine law found for U=0. An analytical expression for the function in the inset can be found in the infinite-U limit, where equation (5) is replaced by a two-level system coupled with a driven cavity mode,

which agrees with the numerical results (see Fig. 3b, inset). The broadening of the dip at φ=π is proportional to γ2/(4J|E|), implying that the visibility goes to zero by increasing the field (〈n2(φ=0)〉→0.5). The behaviour of 〈n2(φ)〉 is again witness to the crossover from the delocalized to the correlated regimes. For large hopping the state of the system is approximately a coherent state. Phases are locked (there are strong fluctuations in the number operator) and the visibility is large. In the opposite case, owing to photon blockade the state is close to a Fock state. Phase fluctuations in the central cavity suppress the global coherence of the system and hence the visibility. We note that, although the functional forms are different, both 〈n2(φ=0)〉 and g2(2)(0) show a crossover that depends only on the dimensionless ratio U/J, as shown in Fig. 3c.

We believe that our results establish the use of photon correlation measurements as effective probes that can reveal the interplay between macroscopic coherence and interactions in strongly correlated photonic systems, and may contain the key to interpret possible phases of driven–dissipative quantum-nonlinear cavity arrays that operate under non-equilibrium conditions.

Methods

The model in equation (1) is reformulated by introducing the canonically transformed bosonic operators and , from which

where we defined Δk=Δ and we discarded the dynamics of the field , which is decoupled from . Rescaled quantities are defined as and . Thus, the dynamics of the full model (1) is equivalent to that of two coupled bosonic fields: is coherently driven, whereas is nonlinear. Losses are taken into account within the quantum master equation in the Born–Markov approximation for the system density matrix, equation (2), for the field operators and with dissipation rates γ and γ2, respectively.

Analytical solution.

An analytical solution to the steady-state master equation can be found in the non-interacting limit, U=0. The equation of motion for a generic operator expectation value, , is , where , and the Liouvillian is written as

Solving for and , respectively, we obtain a system of two coupled equations, from which the steady-state solution is found to be , and hence equation (3).

Numerical solution.

Extensive numerical simulations for the effective model (7) can be carried out fairly efficiently and in a reduced Hilbert space with respect to the full model. After explicitly defining the operators in matrix form on a Fock basis of bosonic number states, the steady-state density matrix for any given set of parameters can be obtained by finding the eigenvector corresponding to the zero eigenvalue of the linear operator equation , where |ρ〉〉 is the density operator mapped into vectorial form, and is the linear matrix corresponding to the Liouvillian operator in the right-hand side of equation (2) (refs 24, 25). Once |ρss〉〉 is obtained from with λss=0, we can recast it in matrix form and calculate any observable in which we are interested. In particular, in this work we deal with , and the steady-state zero-time-delay second-order correlation function . To check convergence with the number of Fock states in the basis as a function of , numerical results for U=0 are compared with equation (3).