Abstract
Blockade interactions whereby a single particle prevents the flow or excitation of other particles provide a mechanism for control of quantum states, including entanglement of two or more particles. Blockade has been observed for electrons1,2,3, photons4 and cold atoms5. Furthermore, dipolar interactions between highly excited atoms have been proposed as a mechanism for ‘Rydberg blockade’6,7, which might provide a novel approach to a number of quantum protocols8,9,10,11. Dipolar interactions between Rydberg atoms were observed several decades ago12 and have been studied recently in a many-body regime using cold atoms13,14,15,16,17,18. However, to harness Rydberg blockade for controlled quantum dynamics, it is necessary to achieve strong interactions between single pairs of atoms. Here, we demonstrate that a single Rydberg-excited rubidium atom blocks excitation of a second atom located more than 10 μm away. The observed probability of double excitation is less than 20%, consistent with a theoretical model of the Rydberg interaction augmented by Monte Carlo simulations that account for experimental imperfections.
Similar content being viewed by others
Main
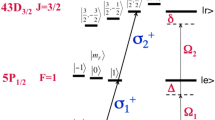
The mechanism of Rydberg blockade is shown in Fig. 1a. Two atoms, one labelled ‘control’ and the other ‘target’, are placed in proximity with each other. The ground state |1〉 and Rydberg state |r〉 of each atom form a two-level system that is coupled by laser beams with Rabi frequency Ω. Application of a 2π pulse (Ω t=2π with t being the pulse duration) on the target atom results in excitation and de-excitation of the target atom giving a phase shift of π on the quantum state, |1〉t→−|1〉t. If the control atom is excited to the Rydberg state before application of the 2π pulse, the dipole–dipole interaction  shifts the Rydberg level by an amount
shifts the Rydberg level by an amount  that detunes the excitation of the target atom so that it is blocked and |1〉t→|1〉t. Thus, the excitation dynamics and phase of the target atom depend on the state of the control atom. Combining this Rydberg-blockade-mediated controlled-phase operation6 with π/2 single-atom rotations between states |0〉t and |1〉t of the target will implement the CNOT gate between two atoms. We have previously demonstrated the ability to carry out ground-state rotations at individual trapping sites19, as well as coherent excitation from ground to Rydberg states at a single site20. Here, we describe experiments that demonstrate the Rydberg blockade effect between two neutral atoms separated by more than 10 μm, which is an enabling step towards creation of entangled atomic states. Previous demonstrations of neutral-atom entanglement have relied on short-range collisions at length scales characterized by a low-energy scattering length of about 10 nm (refs 21, 22). Our results, using laser-cooled and optically trapped 87Rb, extend the distance for strong two-atom interactions by three orders of magnitude, and place us in a regime where the interaction distance is large compared with 1 μm, which is the characteristic wavelength of light needed for internal-state manipulation. The ten-to-one ratio we achieve between the interaction length and the wavelength of the control light is a significant step towards demonstration of a universal quantum gate between neutral atoms in a scalable architecture.
that detunes the excitation of the target atom so that it is blocked and |1〉t→|1〉t. Thus, the excitation dynamics and phase of the target atom depend on the state of the control atom. Combining this Rydberg-blockade-mediated controlled-phase operation6 with π/2 single-atom rotations between states |0〉t and |1〉t of the target will implement the CNOT gate between two atoms. We have previously demonstrated the ability to carry out ground-state rotations at individual trapping sites19, as well as coherent excitation from ground to Rydberg states at a single site20. Here, we describe experiments that demonstrate the Rydberg blockade effect between two neutral atoms separated by more than 10 μm, which is an enabling step towards creation of entangled atomic states. Previous demonstrations of neutral-atom entanglement have relied on short-range collisions at length scales characterized by a low-energy scattering length of about 10 nm (refs 21, 22). Our results, using laser-cooled and optically trapped 87Rb, extend the distance for strong two-atom interactions by three orders of magnitude, and place us in a regime where the interaction distance is large compared with 1 μm, which is the characteristic wavelength of light needed for internal-state manipulation. The ten-to-one ratio we achieve between the interaction length and the wavelength of the control light is a significant step towards demonstration of a universal quantum gate between neutral atoms in a scalable architecture.
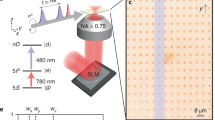
a, Conceptual operation of a Rydberg blockade phase gate between control and target atoms each with internal qubit states |0〉,|1〉 and Rydberg state |r〉. b, Experimental geometry with two trapping regions separated by Z=10 μm. c, Experimental fluorescence image of the atomic density created by averaging 146 exposures each with one atom in the control and target sites.
To carry out the blockade operation of Fig. 1a, the atoms must be close enough to have a strong interaction, yet far enough apart that they can be individually controlled (Fig. 1b). To satisfy these conflicting requirements, we first localize single atoms to regions that are formed by tightly focused beams from a far-detuned laser. The lasers that control the coupling between internal states are focused to a small waist w∼10 μm so the atoms can be separately manipulated by displacing the control lasers, even though the trapping sites are close together. In addition, we excite high-lying Rydberg levels with n=79 and 90. The strength of the long-range interaction between two Rydberg atoms scales as n11, with n being the principal quantum number23. As will be discussed in more detail below, the 79d(90d) Rydberg levels provide  of blockade shift at Z=10.2 μm, which is sufficient for a strong two-atom blockade effect.
of blockade shift at Z=10.2 μm, which is sufficient for a strong two-atom blockade effect.
The experimental apparatus and procedures have been described in our recent publication20, where we observed coherent oscillations between the 87Rb ground and Rydberg levels |1〉≡|5s1/2,f=2,mf=2〉 and |r〉≡|43d5/2,mj=1/2〉. Here, we use similar techniques, but to get a sufficiently strong interaction, we now excite the |r〉≡|79d5/2,mj=1/2〉 or |r〉≡|90d5/2,mj=1/2〉 Rydberg levels. The essential steps of the experimental sequence shown in Fig. 2a are as follows. We start by loading single atoms into one or both sites from a cold background vapour in a magneto-optical trap. Both trapping sites are measured simultaneously by scattering red-detuned molasses light that is near resonant with the 5s1/2−5p3/2 transition and imaging the fluorescence onto a sensitive CCD (charge-coupled device) camera using imaging optics that give an effective pixel size of 2.1×2.1 μm. The counts in regions of interest corresponding to the peaks in Fig. 1c are tabulated and loading of a single atom is established when the counts lie within upper and lower confidence bounds based on histograms of many measurements. The presence of atoms is checked by the first measurement, after which we optically pump the atoms into |1〉. We then turn off the trapping potentials for 8 μs while carrying out the Rydberg excitation, restore the trapping potential and use a second measurement to see whether or not there is still an atom in each site. The trapping light photo-ionizes the Rydberg atoms faster than they can spontaneously decay to the ground state24, which enables detection of Rydberg excitation by monitoring atom loss. As the trap turn-off time is less than the trap vibrational period (radial 15 μs and axial 190 μs), the small probability of atom loss due to turning off the trap is measured to be 3%.
Rabi oscillations between |1〉 and |r〉=|79d5/2,mj=1/2〉 are shown in Fig. 2b when there is no atom present in the control site, and one atom in the target site. The measured and calculated Rabi frequencies agree to about 10%. Figure 2c shows the crosstalk measured at the control site by loading one control atom, no target atoms and keeping the lasers aligned to the target site. The expected Rydberg population due to crosstalk given the Gaussian shape of our excitation lasers is P′∼Ω′2/(Ω′2+Δa.c.2), where Ω′/Ω=e−Z2/wz,7802e−Z2/wz,4802=0.019 is the relative Rabi frequency at the non-addressed site and Δa.c.=2π×2 MHz is our theoretical estimate for the a.c. Stark shift of the |1〉−|r〉 transition. These numbers give P′∼10−4, which is consistent with the observed lack of Rabi oscillations due to spatial crosstalk.
Having verified the ability to carry out Rabi oscillations between |1〉 and |r〉, we use the sequence shown in Fig. 3a to demonstrate Rydberg blockade. We start by loading one atom into each site and then carry out a π pulse |1〉→|r〉 on the control site. A Rydberg pulse of length t is then applied to the target, followed by a second π pulse on the control atom to return it to the ground state. We then measure the population in both sites and keep only the data for which we still have an atom in the control site. This procedure removes spurious data due to cases where the control atom was lost during the initial measurement. Rabi oscillations of the target with no control atom (Fig. 3b) can be compared with the data when there is a control atom present (Fig. 3c). We see that the presence of the control atom reduces the probability of populating the Rydberg state from about 0.8 to 0.3. Figure 3d,e shows equivalent data but with the control and target roles switched between the two trapping sites. This verifies that the results are not due to some spatial asymmetry or bias in our experimental procedures.
a, Experimental sequence. b, Rabi oscillations on site 2 when no π pulses are applied to site 1. c, Blockaded oscillations on site 2 when the π pulses are applied to site 1. d,e, The same as in b,c, but with the roles of sites 1 and 2 reversed. The red lines are curve fits to the function (1−a)+acos(2πf t)e−t/τ. The fit parameters (a,f (MHz),τ (μs)) were: (0.44, 0.51, 5.7) for b, (0.17, 0.45, 3.0) for c, ( ) for d and (0.21, 0.45, 2.3) for e. The error bars are standard deviations with 50 data points at each value of t.
) for d and (0.21, 0.45, 2.3) for e. The error bars are standard deviations with 50 data points at each value of t.
To confirm that the observed excitation suppression is due to Rydberg blockade, we must account quantitatively for the strength of the Rydberg interactions. 87Rb atoms excited to the 79d5/2 state experience a Förster interaction25,26 that is dominated by the near degeneracy of the energy of two 79d atoms with the energy of a two-atom state npp+nff. The interaction is strongest for channels with26 np=80,nf=78 and np=81,nf=77. The situation is complicated by the fact that the B0=1.15 mT bias magnetic field that is used for optical pumping remains on during the Rydberg interaction, giving Zeeman shifts and coupling of different fine-structure states. This leads to mixing of the 79d5/2 and 79d3/2 fine-structure manifolds, which have a zero-field separation of only about 23 MHz. In this situation, our previously developed analytical theory of the Förster interaction26 no longer applies, so we have solved the problem numerically accounting for a total of 436 coupled molecular states. The Rydberg interaction can be characterized by two numbers: the probability of two-atom excitation after a π pulse on the target atom P2, and the effective blockade shift  . We calculate P2 numerically using the molecular energies and wavefunctions, as discussed in Supplementary Information, Section S2, and then determine the effective blockade shift from the relation
. We calculate P2 numerically using the molecular energies and wavefunctions, as discussed in Supplementary Information, Section S2, and then determine the effective blockade shift from the relation  .
.
The theoretical blockade shifts and double-excitation probabilities for a 1.15 mT magnetic field with the observed excitation Rabi frequency of Ω/2π=0.51 MHz are shown in Fig. 4. Averaging over the probability distribution of y1−y2, we predict a double-excitation probability of  This value of
This value of  in turn implies an average blockade shift of
in turn implies an average blockade shift of  . Monte Carlo simulations of the blockade experiment accounting for random variations of atomic position, Doppler broadening and the calculated position-dependent blockade shift discussed above, but without allowing for any extra experimental errors, predict P2∼0.14, as shown in Supplementary Information, Fig. S4.
. Monte Carlo simulations of the blockade experiment accounting for random variations of atomic position, Doppler broadening and the calculated position-dependent blockade shift discussed above, but without allowing for any extra experimental errors, predict P2∼0.14, as shown in Supplementary Information, Fig. S4.
On the other hand, the data in Fig. 3 show double-excitation probabilities in the blockaded case as high as P2∼0.3−0.35, which is about three times higher than the calculated  . To understand the cause of this difference, we have carried out extra Monte Carlo simulations of the three-pulse blockade sequence including imperfections in state measurement, state preparation and Rydberg detection. As described in detail in Supplementary Information, Section S3, the primary causes of the reduced blockade efficiency observed experimentally are attributable to loss of atoms during the first measurement (probability 1−ηm∼0.15), imperfect state preparation (optical pumping efficiency of ηp∼0.90) and imperfect Rydberg detection efficiency (error probability ηRd∼0.05). Using these values together with the full set of experimental parameters discussed above, we predict unblockaded Rabi oscillations to Rydberg levels with peak-to-peak oscillation amplitude of 2a∼0.80 and blockaded oscillations with peak-to-peak amplitude of 2a∼0.32. These numbers agree to within a few per cent with the experimental data in Figs 2 and 3.
. To understand the cause of this difference, we have carried out extra Monte Carlo simulations of the three-pulse blockade sequence including imperfections in state measurement, state preparation and Rydberg detection. As described in detail in Supplementary Information, Section S3, the primary causes of the reduced blockade efficiency observed experimentally are attributable to loss of atoms during the first measurement (probability 1−ηm∼0.15), imperfect state preparation (optical pumping efficiency of ηp∼0.90) and imperfect Rydberg detection efficiency (error probability ηRd∼0.05). Using these values together with the full set of experimental parameters discussed above, we predict unblockaded Rabi oscillations to Rydberg levels with peak-to-peak oscillation amplitude of 2a∼0.80 and blockaded oscillations with peak-to-peak amplitude of 2a∼0.32. These numbers agree to within a few per cent with the experimental data in Figs 2 and 3.
Our simulations show that the primary causes of imperfect blockade are experimental imperfections in state preparation and measurement as well as variations in the two-atom separation at finite temperature. We expect that modest improvements to the experimental apparatus will enable blockade errors to be reduced, which will then lead to the possibility of observing a long-range two-atom conditional logic gate. Indeed, a detailed analysis of a Rydberg blockade CNOT gate taking into account a large number of experimental imperfections suggests that gate errors at the 10−3 level are feasible24. As a next step in this direction, Fig. 5a shows extra blockade data obtained by excitation of 90d5/2, with all other parameters as in Fig. 3. As shown in Fig. 4, and discussed in Supplementary Information, the Rydberg interaction strength for n=90 is about three times stronger than for n=79. With this strong an interaction, the observed probability of excitation of a target atom is reduced to under 20%. The spatially averaged theoretical double-excitation probability, without accounting for experimental imperfections, is reduced to  . Thus, the observed blockade leakage is almost entirely due to errors in state preparation and measurement, as demonstrated by the Monte Carlo simulation shown in Fig. 5b. We therefore expect that technical improvements to reduce these errors will result in high-fidelity Rydberg blockade that will be suitable for precise quantum logic operations.
. Thus, the observed blockade leakage is almost entirely due to errors in state preparation and measurement, as demonstrated by the Monte Carlo simulation shown in Fig. 5b. We therefore expect that technical improvements to reduce these errors will result in high-fidelity Rydberg blockade that will be suitable for precise quantum logic operations.
In summary, we have observed Rydberg blockade between two atoms localized in spatially separated trapping sites. The excitation of one atom to a Rydberg level blocks the subsequent excitation of a second atom. The blockade effectiveness is consistent with calculations of the Rydberg interaction strength accounting for all experimental parameters. Our observations complement previous work on excitation suppression in a many-body regime13,14,15,16,17,18 and extend the range of strong interactions between just two atoms to a distance that is ten times larger than the wavelength of the light needed for internal-state manipulation. We believe this will be important for ongoing efforts to build scalable neutral-atom quantum logic devices. In future work, we plan to combine the blockade studied here with single-atom rotations to demonstrate a universal CNOT gate between two atoms, which may eventually form the basis for a many-qubit quantum processor.
After completion of this work, we became aware of a related preprint by A. Gaëtan et al. 27.
Methods
Experimental geometry.
Single atoms are localized in far-off-resonance traps created by focusing a laser with wavelength λ=1,064 nm, to spots with waists (1/e2 intensity radius) w=3.0 μm. The resulting traps have a potential depth of U/kB=4.1 mK. The trapped atoms have a measured temperature of T≃180 μK. The position probability distributions for each atom are well described by quasi-one-dimensional Gaussians with σz=0.32 μm and σy=4.0 μm. The resulting single-atom distributions observed experimentally by viewing along the x axis are shown in Fig. 1c. The observed spatial probability distributions are broader than the above estimates owing to the finite resolution of our imaging optics. Measurement and analysis procedures used to determine the point spread function of the imaging optics (σopt∼1.5 μm) as well as the spatial distribution and temperature of the trapped atoms are described in Supplementary Information.
Single-atom Rabi oscillations.
States |1〉,|r〉 are coupled by two-photon transitions driven by counterpropagating 780 and 480 nm lasers polarized along  , which is also the direction of the 1.15 mT bias magnetic field. Each laser is focused to a waist of w∼10 μm and the light of each colour is switched between control and target sites using acousto-optic modulators (AOMs). The frequency shifts of the 780 and 480 nm beams that occur due to AOM switching have opposite signs so that the sum frequency that is resonant with the Rydberg level is the same at both sites.
, which is also the direction of the 1.15 mT bias magnetic field. Each laser is focused to a waist of w∼10 μm and the light of each colour is switched between control and target sites using acousto-optic modulators (AOMs). The frequency shifts of the 780 and 480 nm beams that occur due to AOM switching have opposite signs so that the sum frequency that is resonant with the Rydberg level is the same at both sites.
The Rabi pulse length t is defined by a 780 nm laser that is switched with a fast AOM (20 ns rise time). The 480 nm light is switched more slowly, before and after each pulse. Each data point is the average of ∼50 pre-selected single-atom experiments, with the bars showing ±1 standard deviation. The solid line in Fig. 2b shows a curve fitted to the data with the function (1−a)+ae−t/τcos(Ω t), which gives a Rabi frequency of Ω=2π×0.51 MHz.
The theoretical two-photon Rabi frequency is Ω=CΔΩ780Ω480/2Δ. Starting from the |f=2,mf=2〉 ground state with  light,
light,  ,
,  and CΔ=(Δ−Δ23/2)/(Δ−Δ23), with Δ23/2π=−0.267 GHz being the hyperfine splitting of the 5p3/2 f=2,3 levels and Δ being the laser detuning from |5p3/2,f=3〉. Using quantum defect wavefunctions, we find R5s1/25p3/2=5.14a0,R5p3/279d5/2=0.012a0. Experimental parameters of Δ/2π=−2.4 GHz, beam powers of P780=1.95 μW, P480=26.2 mW and waists wx,780=11.9, wz,780=7.0, wx,480=11.3,wz,480=9.0 μm give Ω/2π=0.61 MHz. This is then reduced by 3.7% to account for the Zeeman mixing of the 79d5/2 state with 79d3/2, which has a negligible radial matrix element with 5p3/2. The final result, with no adjustable parameters, is Ω/2π=0.59 MHz.
and CΔ=(Δ−Δ23/2)/(Δ−Δ23), with Δ23/2π=−0.267 GHz being the hyperfine splitting of the 5p3/2 f=2,3 levels and Δ being the laser detuning from |5p3/2,f=3〉. Using quantum defect wavefunctions, we find R5s1/25p3/2=5.14a0,R5p3/279d5/2=0.012a0. Experimental parameters of Δ/2π=−2.4 GHz, beam powers of P780=1.95 μW, P480=26.2 mW and waists wx,780=11.9, wz,780=7.0, wx,480=11.3,wz,480=9.0 μm give Ω/2π=0.61 MHz. This is then reduced by 3.7% to account for the Zeeman mixing of the 79d5/2 state with 79d3/2, which has a negligible radial matrix element with 5p3/2. The final result, with no adjustable parameters, is Ω/2π=0.59 MHz.
We attribute the approximately 14% lower experimental value to some spatial misalignment, and a small fraction of the Rydberg excitation light being present in servo sidebands from laser locks. The data show that the atom is returned to the ground state with 95% probability after one cycle and that Rydberg-state excitation is achieved with ∼80% probability. The lack of perfect Rydberg excitation is attributed to errors in state preparation and measurement discussed in Supplementary Information. The laser linewidths as deduced from Allan variance measurements are <500 Hz, relative to a common reference cavity over timescales of 10 μs. We do not believe the finite linewidths have a significant influence on the Rydberg excitation probability.
References
Fulton, T. A. & Dolan, G. J. Observation of single-electron charging effects in small tunnel junctions. Phys. Rev. Lett. 59, 109–112 (1987).
Averin, D. V. & Likharev, K. K. Coulomb blockade of single-electron tunneling, and coherent oscillations in small tunnel-junctions. J. Low. Temp. Phys. 62, 345–373 (1986).
Ono, K., Austing, D. G., Tokura, Y. & Tarucha, S. Current rectification by Pauli exclusion in a weakly coupled double quantum dot system. Science 297, 1313–1317 (2002).
Birnbaum, K. M. et al. Photon blockade in an optical cavity with one trapped atom. Nature 436, 87–90 (2005).
Schlosser, N., Reymond, G., Protsenko, I. & Grangier, P. Sub-poissonian loading of single atoms in a microscopic dipole trap. Nature 411, 1024–1027 (2001).
Jaksch, D. et al. Fast quantum gates for neutral atoms. Phys. Rev. Lett. 85, 2208–2211 (2000).
Lukin, M. D. et al. Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 87, 037901 (2001).
Saffman, M. & Walker, T. G. Creating single atom and single photon sources from entangled atomic ensembles. Phys. Rev. A 66, 065403 (2002).
Saffman, M. & Walker, T. G. Entangling single- and n-atom qubits for fast quantum state detection and transmission. Phys. Rev. A 72, 042302 (2005).
Brion, E., Mouritzen, A. S. & Mølmer, K. Conditional dynamics induced by new configurations for Rydberg dipole–dipole interactions. Phys. Rev. A 76, 022334 (2007).
Brion, E., Mølmer, K. & Saffman, M. Quantum computing with collective ensembles of multilevel systems. Phys. Rev. Lett. 99, 260501 (2007).
Raimond, J. M., Vitrant, G. & Haroche, S. Spectral line broadening due to the interaction between very excited atoms: ‘the dense Rydberg gas’. J. Phys. B 14, L655–L660 (1981).
Tong, D. et al. Local blockade of Rydberg excitation in an ultracold gas. Phys. Rev. Lett. 93, 063001 (2004).
Singer, K., Reetz-Lamour, M., Amthor, T., Marcassa, L. G. & Weidemüller, M. Suppression of excitation and spectral broadening induced by interactions in a cold gas of Rydberg atoms. Phys. Rev. Lett. 93, 163001 (2004).
Liebisch, T. C., Reinhard, A., Berman, P. R. & Raithel, G. Atom counting statistics in ensembles of interacting Rydberg atoms. Phys. Rev. Lett. 95 253002 (2005); erratum 98, 109903 (2007).
Vogt, T. et al. Dipole blockade at Förster resonances in high resolution laser excitation of Rydberg states of cesium atoms. Phys. Rev. Lett. 97, 083003 (2006).
Bohlouli-Zanjani, P., Petrus, J. A. & Martin, J. D. D. Enhancement of Rydberg atom interactions using ac stark shifts. Phys. Rev. Lett. 98, 203005 (2007).
Heidemann, R. et al. Evidence for coherent collective Rydberg excitation in the strong blockade regime. Phys. Rev. Lett. 99, 163601 (2007).
Yavuz, D. D. et al. Fast ground state manipulation of neutral atoms in microscopic optical traps. Phys. Rev. Lett. 96, 063001 (2006).
Johnson, T. A. et al. Rabi oscillations between ground and Rydberg states with dipole–dipole atomic interactions. Phys. Rev. Lett. 100, 113003 (2008).
Mandel, O. et al. Controlled collisions for multiparticle entanglement of optically trapped atoms. Nature 425, 937–940 (2003).
Anderlini, M. et al. Controlled exchange interaction between pairs of neutral atoms in an optical lattice. Nature 448, 452–456 (2007).
Gallagher, T. F. Rydberg Atoms (Cambridge Univ. Press, 1994).
Saffman, M. & Walker, T. G. Analysis of a quantum logic device based on dipole–dipole interactions of optically trapped Rydberg atoms. Phys. Rev. A 72, 022347 (2005).
Förster, T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. d. Physik 437, 55–75 (1948).
Walker, T. G. & Saffman, M. Consequences of Zeeman degeneracy for the van der Waals blockade between Rydberg atoms. Phys. Rev. A 77, 032723 (2008).
Gaëtan, A. et al. Observation of collective excitation of two individual atoms in the Rydberg blockade regime. Natue Phys. 5, doi:10.1038/nphys1183.
Acknowledgements
This work was supported by the NSF and ARO-IARPA.
Author information
Authors and Affiliations
Contributions
The experimental work was carried out by E.U. and T.A.J. (who contributed equally) with assistance by T.H., L.I. and D.D.Y. Data analysis and blockade simulations were carried out by T.A.J. and M.S., calculations of Rydberg interactions were carried out by T.G.W. and M.S. and the experiment was planned and designed by T.G.W. and M.S.
Corresponding author
Supplementary information
Supplementary Information
Supplementary Informations (PDF 348 kb)
Rights and permissions
About this article
Cite this article
Urban, E., Johnson, T., Henage, T. et al. Observation of Rydberg blockade between two atoms. Nature Phys 5, 110–114 (2009). https://doi.org/10.1038/nphys1178
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1178
This article is cited by
-
Quantum computing dataset of maximum independent set problem on king lattice of over hundred Rydberg atoms
Scientific Data (2024)
-
Floquet-tailored Rydberg interactions
Nature Communications (2023)
-
Trimer quantum spin liquid in a honeycomb array of Rydberg atoms
Communications Physics (2023)
-
Quantum computing with Rydberg atom graphs
Journal of the Korean Physical Society (2023)
-
Observation of a molecular bond between ions and Rydberg atoms
Nature (2022)