Abstract
The notion of quantum spin-liquids (QSLs), antiferromagnets with quantum fluctuation-driven disordered ground states, is now firmly established in one-dimensional (1D) spin systems as well as in their ladder cousins. The spin-1/2 organic insulator κ-(bis(ethylenedithio)-tetrathiafulvalene)2Cu2(CN)3 (κ-(BEDT-TTF)2Cu2(CN)3; ref. 1) with a 2D triangular lattice structure is very likely to be the first experimental realization of this exotic state in D≥2. Of crucial importance is to unveil the nature of the low-lying elementary spin excitations2,3, particularly the presence/absence of a ‘spin gap’, which will provide vital information on the universality class of this putative QSL. Here, we report on our thermal-transport measurements carried out down to 80 mK. We find, rather unexpectedly, unambiguous evidence for the absence of a gapless excitation, which sharply contradicts recent reports of heat capacity measurements4. The low-energy physics of this intriguing system needs be reinterpreted in light of the present results indicating a spin-gapped QSL phase.
Similar content being viewed by others
Main
In antiferromagnetically coupled spin systems, geometrical frustrations enhance quantum fluctuations. Largely triggered by the proposal of the resonating-valence-bond theory for S=1/2 degrees of freedom residing on a frustrated two-dimensional (2D) triangular lattice5,6,7 and its possible application to high-Tc cuprates with a doped 2D square lattice8,9, realizing/detecting QSLs in 2D systems has been a long-sought goal. Recently, discoveries of QSL states on S=1/2 triangular lattices have been reported in organic compounds, κ-(BEDT-TTF)2Cu2(CN)3 (Fig. 1, inset)1,10,11, C2H5(CH3)3Sb[Pd(1,3-dithiole-2-thione-4,5-dithiolate)2]2 (ref. 12) and 3He thin film on graphite13. In particular, the NMR spectrum of κ-(BEDT-TTF)2Cu2(CN)3 exhibits no signs of magnetic ordering down to ∼30 mK, which is some four orders of magnitude below the exchange coupling J∼250 K (refs 1, 11). These findings aroused great interest because it is generally believed that whereas a QSL state is realized in the strongly frustrated S=1/2 2D kagome lattice14, which can be viewed as corner-sharing triangles, the classical magnetically ordered state is stable in the less frustrated isotropic Heisenberg triangular lattice15,16. Several ideas, such as a Hubbard model with a moderate onsite repulsion17, a ring exchange model18 and one-dimensionalization by a slight distortion from the isotropic triangular lattice19,20, have been put forth to explain the absence of the long-range magnetic ordering in κ-(BEDT-TTF)2Cu2(CN)3. Nevertheless, the origin for the QSL state remains unresolved.
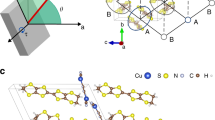
κ(T) in zero field for two different single crystals of deuterated κ-(BEDT-TTF)2Cu2(CN)3 (sample A and sample B) measured in a 3He cryostat (black for sample A and green for sample B) and dilution refrigerator (blue for sample A and light green for sample B). As the temperature is lowered, κ(T) decreases and exhibits a broad hump starting to increase at around T*≃6 K. Inset: The crystal structure of a two-dimensional BEDT-TTF layer of κ-(BEDT-TTF)2Cu2(CN)3 viewed along the long axes of BEDT-TTF molecules. Pairs of BEDT-TTF molecules form dimers arranged in a triangular lattice in terms of transfer integrals t and t′ between the dimers. The ratio of transfer integrals is nearly unity11 and the spin-1/2 nearly isotropic triangular lattice is realized1.
To understand the nature of novel QSL states, knowledge on the structure of the low-lying excitation spectrum in the zero-temperature limit, particularly the absence/presence of a spin gap, is indispensable, bearing immediate implications on the spin correlations of the ground state, as well as on the quantum numbers carried by each elementary excitation. For instance in 1D, half-integer spin Heisenberg chains feature a massless spectrum, which enables proliferation of low-energy spinon excitations, whereas such excitations are suppressed in the integer spin case, which has a massive spectrum21.
As it is not possible to directly probe the microscopic spin structure using neutron scattering owing to the compound’s organic nature, thermodynamic measurements must be adopted to unveil the low-lying excitation of κ-(BEDT-TTF)2Cu2(CN)3. Very recent specific-heat measurements of κ-(BEDT-TTF)2Cu2(CN)3 show a large linear temperature-dependent contribution, γ∼15 mJ K−2 mol−1 (ref. 4), which suggests the presence of gapless excitations, similar to the electronic specific heat in metals. This observation provides strong support for several theoretical models, including a QSL with gapless ‘spinons’, which, like its 1D predecessors are (fermionic) elementary excitations that carry spin-1/2 and zero charge2,3, which are to be compared with conventional (bosonic) magnons that carry spin-1. However, it is premature to conclude that the QSL in κ-(BEDT-TTF)2Cu2(CN)3 is gapless from these measurements because the specific-heat data are plagued by a very large nuclear Schottky contribution below 1 K (ref. 4), which would necessarily lead to ambiguity. Incorporation of a probe that is free from such a contamination is strongly required22.
As pointed out in ref. 3, thermal conductivity (κ) measurements are highly advantageous as probes of elementary excitations in QSLs, because κ is sensitive exclusively to itinerant excitations and is totally insensitive to localized entities such as are responsible for Schottky contributions. The heat is carried primarily by acoustic phonons (κph) and magnetic contributions (κmag). Indeed, a large magnetic contribution to the heat current is observed in low-dimensional spin systems23,24.
As shown in Fig. 1, the thermal conductivity exhibits an unusual behaviour characterized by a hump structure around T*≃6 K. A similar hump is observed in the magnetic part of the specific heat4 and NMR relaxation rate1,10 around T*, although no structural transition has been detected. These results obviously indicate that κmag occupies a substantial portion in κ. Various scenarios, such as a crossover to a QSL state4, a phase transition associated with the pairing of spinons2, spin-chirality ordering25, Z2 vortex formation26 and exciton condensation27, have been suggested as a possible source of the anomaly at T* and warrant further studies.
The thermal conductivity at μ0H=0 and 10 T in the low-temperature regime (T<300 mK) is shown in Fig. 2. A striking deviation of κ/T from a T2 dependence is observed for both samples; both curves exhibit a convex trend. At such low temperatures, the mean free path of phonons is as long as the crystal size and κph/T has a T2 dependence, which has indeed been reported in a similar compound κ-(BEDT-TTF)2Cu(NCS)2 (ref. 28). Therefore, the observed non-T2 dependence, together with the fact that κ is enhanced by magnetic field, definitely indicates the substantial contribution of κmag in κ even in this T range.
Thermal conductivity divided by temperature plotted as a function of T2 below 300 mK in zero field (blue for sample A and green for sample B) and at μ0H=10 T (red, sample A) applied perpendicular to the basal plane. Convex and non-T2 dependent κ/T is observed for both crystals. κ/T of sample A at 10 T shows a nearly parallel shift from that in zero field. It is immediately obvious that κ/T for all data vanishes as extrapolating to T→0 K, indicating the absence of the gapless fermionic excitations. This is in sharp contrast to the specific-heat measurements, which claim the presence of gapless excitations4.
The results shown in Fig. 2 provide key information on the elementary excitations from the QSL state of κ-(BEDT-TTF)2Cu2(CN)3. Most importantly, it is extremely improbable from the experimental data that κ/T in the T→0 K regime has a finite residual value for data of both samples in zero field and that of sample A under 10 T. (Indeed, a simple extrapolation of both data in zero field even gives a negative intersect.) These results lead us to conclude that κ/T vanishes at T=0 K. It should be stressed that the vanishing κ/T immediately indicates the absence of low-lying fermionic excitations, in sharp contrast to the finite γ term reported in the heat capacity measurements4. We believe that the heat capacity measurements incorrectly suggest the presence of gapless excitation, possibly owing to the large Schottky contribution at low temperatures.
The present conclusion is reinforced by comparing the data with the thermal conductivity calculated by assuming a spinon Fermi surface with gapless excitations3, which is given as

where εF is the Fermi energy, m is the electron mass, A is the unit cell area of the layer, d is the interlayer distance and τ is the impurity scattering time. Estimating εF=J as in 1D spin systems29, we compare our result with equation (1) as shown in Fig. 3. It is evident that equation (1) yields κ/T that increases with decreasing T for both clean and dirty cases and is opposite to the observation. Moreover, to obtain the same magnitude of κ/T in this model at the lowest temperature, we need to assume that the mean free path is only a few times longer than the lattice constant a. However, such a large concentration of the impurity is highly unlikely in this clean system1. Thus, the theory based on a gapless fermionic spinon picture is incompatible with the present results, although it may be applicable to other systems.
Having established the absence of the low-lying fermionic excitations, we turn to a more detailed analysis of the T dependence of κ. As seen in the inset of Fig. 4, where logκmag is plotted against logT, κmag does not show a power-law dependence on T. As the precise value of κph is unknown, κmag(=κ−κph) is estimated for several values of κph. For each case, no linear relation is observed in this log–log plot. It should be noted that when κph is increased, the nonlinearity becomes more pronounced. This is also manifested by the index n=(dlogκ/dlogT) plotted in the same figure where n increases steeply with decreasing temperature, and subtracting κph from the observed κ even enhances the non-power-law behaviour. Thus, in spite of the ambiguity for estimating κph, we can safely conclude that κmag at low temperatures does not exhibit a power-law temperature dependence. These results place further constraints on the theoretical description of the excitation spectrum; for example, the nodal excitations that may be expected in systems with an anisotropic gap structure2 which will give rise to a power-law dependence of κ on T, in analogy to the quasiparticles in d-wave superconductors, are also absent.
Inset: logκmag (sample A) in zero field plotted against logT estimated for several values of κph (=0 (blue), 1/2 (green) and 3/4 (orange) of κ at 100 mK) assuming a cubic temperature dependence of κph. In the same figure, the exponent n=(dlogκ/dlogT) obtained by assuming a power-law dependence of κ∝Tn is also plotted (κph=0 (blue), 1/2 (green), 3/4 (orange) of κ at 100 mK). Main panel: An Arrhenius plot of κ of sample A (κ∝exp(−Δ/kBT)) in zero field and at μ0H=10 T. Activation-type behaviour can be seen for both data. The dashed–dotted and dotted lines are fits to equation (1) with α=0.12 W K−1 m−1, β=0.51 W K−4 m−1 and Δ=0.46 K for 0 T, and with α=0.081 W K−1 m−1, β=0.64 W K−4 m−1 and Δ=0.38 K for 10 T, respectively. The green and orange show the same data as in the inset and the fittings for α e−Δ/kBT give α=0.087 W K−1 m−1, Δ=0.45 K and α=0.048 W K−1 m−1, Δ=0.43 K, respectively.
The absence of the gapless excitation implies the presence of a spin gap in the excitation spectrum. To estimate the magnitude of the spin gap, we try to fit the data to

as shown in an Arrhenius plot in Fig. 4. The best fit for the 0 (10) T data gives Δ=0.46 (0.38) K and a β-value that implies that κph is roughly 1/4 of the total κ at 100 mK. We note that the amplitude of Δ is little affected by the choice of κph (see Fig. 4). As the Arrhenius-type behaviour is observed in only one order range of κ, the estimation of the gap size may have a large ambiguity. Nevertheless, we can safely conclude that the estimated gap value from Fig. 4 is strikingly small compared with J (Δ∼J/500) and insensitive to magnetic fields.
This field insensitivity is consistent with a theory of a gapped QSL (ref. 7) with a finite energy gap for both magnetic and non-magnetic excitations. On the other hand, the tiny gap value may alternatively be attributed to a proximity to a quantum critical point of Z2 spin-liquid27, or as a result of a slight anisotropy of J (ref. 19). However, at present, the origin of the spin gap is an open question. It is tempting to associate the extremely small gap value with kBT*(≪J) (instead of to J itself), which may be a characteristic temperature of the QSL of κ-(BEDT-TTF)2Cu2(CN)3. In any case, our low-temperature thermal-transport measurements demonstrate that the fermionic spinons, if present, will experience an instability in this system, which will generate a small gap in the spin excitation spectrum.
Methods
κ-(BEDT-TTF)2Cu2(CN)3 single crystals were grown by the electrochemical method. The thermal conductivity was measured by a standard steady-state method with a one-heater–two-thermometer configuration in 3He and dilution refrigerators. The thermal current was applied within the 2D plane and the magnetic field was applied perpendicular to the plane. We have measured several deuterated and non-deuterated crystals and observed no significant sample dependence. It has been reported that in superconductors, thermal decoupling between the electron and phonon conductions can be caused by the poor contacts at very low temperatures30. It could be argued that such a decoupling may occur in the phonons and the spinons, and may lead to apparent absence of finite κ/T at T→0 K. However, we note that this is inconsistent with the observed increase of κ with H (shown in Supplementary Information). Because the magnetic field decreases the number of spinons, κ should decrease with H owing to the further reduction of the coupling. Moreover, we measured the thermal conductivity on the samples with the contact resistance ranging from 1 to 20 Ω and found no serious difference in the thermal conductivity at low temperatures.
References
Shimizu, Y., Miyagawa, K., Kanoda, K., Maesato, M. & Saito, G. Spin liquid state in an organic Mott insulator with a triangular lattice. Phys. Rev. Lett. 91, 107001 (2003).
Lee, S.-S., Lee, P. A. & Senthil, T. Amperean pairing instability in the U(1) spin liquid state with fermi surface and application to κ-(BEDT-TTF)2Cu2(CN)3 . Phys. Rev. Lett. 98, 067006 (2007).
Nave, C. P. & Lee, P. A. Transport properties of a spinon Fermi surface coupled to a U(1) gauge field. Phys. Rev. B 76, 235124 (2007).
Yamashita, S. et al. Thermodynamic properties of a spin-1/2 spin-liquid state in a κ-type organic salt. Nature Phys. 4, 459–462 (2008).
Anderson, P.W. Resonating valence bonds: A new kind of insulator? Mater. Res. Bull. 8, 153–160 (1973).
Kalmeyer, V & Laughlin, R. B. Equivalence of the resonating-valence-bond and fractional quantum hall states. Phys. Rev. Lett. 59, 2095–2098 (1987).
Moessner, R. & Sondhi, S. L. Resonating valence bond phase in the triangular lattice quantum dimer model. Phys. Rev. Lett. 86, 1881–1884 (2001).
Anderson, P.W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).
Powell, B. J. & McKenzie, R. H. Symmetry of the superconducting order parameter in frustrated systems determined by the spatial anisotropy of spin correlations. Phys. Rev. Lett. 98, 027005 (2007).
Shimizu, Y., Miyagawa, K., Kanoda, K., Maesato, M. & Saito, G. Emergence of inhomogeneous moments from spin liquid in the triangular-lattice Mott insulator κ-(ET)2Cu2(CN)3 . Phys. Rev. B 73, 140407(R) (2006).
Zheng, W., Singh, R. R. P., McKenzie, R. H. & Coldea, R. Temperature dependence of the magnetic susceptibility for triangular-lattice antiferromagnets with spatially anisotropic exchange constants. Phys. Rev. B 71, 134422 (2005).
Itou, T., Oyamada, A., Maegawa, S., Tamura, M. & Kato, R. Quantum spin liquid in the spin-1/2 triangular antiferromagnet EtMe3Sb[Pd(dmit)2]2 . Phys. Rev. B 77, 104413 (2008).
Masutomi, R., Karaki, Y. & Ishimoto, H. Gapless spin liquid behavior in two-dimensional solid 3He. Phys. Rev. Lett. 92, 025301 (2004).
Waldtmann, Ch. et al. First excitations of the spin 1/2 Heisenberg antiferromagnet on the kagome lattice. Eur. Phys. J. B 2, 501–507 (1998).
Huse, D. A. & Elser, V. Simple variational wave functions for two-dimensional Heisenberg spin- antiferromagnets. Phys. Rev. Lett. 60, 2531–2534 (1988).
Capriotti, L., Trumper, A. E. & Sorella, S. Long-range Néel order in the triangular Heisenberg model. Phys. Rev. Lett. 82, 3899–3902 (1999).
Morita, H., Watanabe, S. & Imada, M. Nonmagnetic insulating states near the Mott transitions on lattices with geometrical frustration and implications for κ-(ET)2Cu2(CN)3 . J. Phys. Soc. Jpn. 71, 2109–2112 (2002).
Misguich, G., Lhuillier, C., Bernu, B. & Waldtmann, C. Spin-liquid phase of the multiple-spin exchange Hamiltonian on the triangular lattice. Phys. Rev. B 60, 1064–1074 (1999).
Yunoki, S. & Sorella, S. Two spin liquid phases in the spatially anisotropic triangular Heisenberg model. Phys. Rev. B 74, 014408 (2006).
Hayashi, Y. & Ogata, M. Possibility of gapless spin liquid state by one-dimensionalization. J. Phys. Soc. Jpn. 76, 053705 (2007).
Haldane, F. D. M. Nonlinear field theory of large-spin Heisenberg antiferromagnets: Semiclassically quantized solitons of the one-dimensional easy-axis Néel state. Phys. Rev. Lett. 50, 1153–1156 (1983).
Ramirez, A. P. Quantum spin liquids: A flood or a trickle?. Nature Phys. 4, 442–443 (2008).
Sales, B. C., Lumsden, M. D., Nagler, S. E., Mandrus, D. & Jin, R. Magnetic field enhancement of heat transport in the 2D Heisenberg antiferromagnet K2V3O8 . Phys. Rev. Lett. 88, 095901 (2002).
Li, S. Y., Taillefer, L., Wang, C. H. & Chen, X. H. Ballistic magnon transport and phonon scattering in the antiferromagnet Nd2CuO4 . Phys. Rev. Lett. 95, 156603 (2005).
Baskaran, G. Novel local symmetries and chiral-symmetry-broken phases in triangular-lattice Heisenberg model. Phys. Rev. Lett. 63, 2524–2527 (1989).
Kawamura, H. & Miyashita, S. Phase transition of the two-dimensional Heisenberg antiferromagnet on the triangular lattice. J. Phys. Soc. Jpn. 53, 4138–4154 (1984).
Qi, Y. & Sachdev, S. Insulator–metal transition on the triangular lattice. Phys. Rev. B 77, 165112 (2008).
Belin, S., Behnia, K. & Deluzet, A. Heat conduction in κ-(BEDT-TTF)2Cu(NCS)2 . Phys. Rev. Lett. 81, 4728–4731 (1998).
Luther, A. & Peschel, I. Calculation of critical exponents in two dimensions from quantum field theory in one-dimension. Phys. Rev. B 12, 3908–3917 (1975).
Smith, M. F., Paglione, J., Walker, M. B. & Taillefer, L. Origin of anomalous low-temperature downturns in the thermal conductivity of cuprates. Phys. Rev. B 71, 014506 (2005).
Acknowledgements
We would like to thank G. Baskaran, L. N. Bulaevskii, Y. Hayashi, N. Kawakami, H. Kawamura, Y. Nakazawa, S. Sachdev, A. Tanaka and S. Watanabe for valuable discussion. This work was supported by Grants-in-Aid (No. 20224008 and No. 20840026) from JSPS and a Grant-in-Aid for the Global COE Program ‘The Next Generation of Physics, Spun from Universality and Emergence’ from MEXT of Japan.
Author information
Authors and Affiliations
Contributions
M.Y., N.N., Y.K., T. Shibauchi and Y.M. carried out measurements, data analysis and discussion. T. Sasaki, N.Y. and N.K. prepared the samples. S.F. gave theoretical advice.
Corresponding author
Supplementary information
Supplementary Information
Supplementary Informations (PDF 78 kb)
Rights and permissions
About this article
Cite this article
Yamashita, M., Nakata, N., Kasahara, Y. et al. Thermal-transport measurements in a quantum spin-liquid state of the frustrated triangular magnet κ-(BEDT-TTF)2Cu2(CN)3. Nature Phys 5, 44–47 (2009). https://doi.org/10.1038/nphys1134
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1134
This article is cited by
-
Chasing the spin gap through the phase diagram of a frustrated Mott insulator
Nature Communications (2023)
-
Thermally-robust spatiotemporal parallel reservoir computing by frequency filtering in frustrated magnets
Scientific Reports (2023)
-
Resistivity and thermal conductivity of an organic insulator β′–EtMe3Sb[Pd(dmit)2]2
Scientific Reports (2022)
-
Emergent quasiparticles at Luttinger surfaces
Nature Communications (2022)
-
Giant isotropic magneto-thermal conductivity of metallic spin liquid candidate Pr2Ir2O7 with quantum criticality
Nature Communications (2021)