Abstract
One of the grand challenges of contemporary physics is understanding strongly interacting quantum systems comprising such diverse examples as ultracold atoms in traps, electrons in high-temperature superconductors and nuclear matter1. Warm dense matter, defined by temperatures of a few electron volts and densities comparable with solids, is a complex state of such interacting matter2. Moreover, the study of warm dense matter states has practical applications for controlled thermonuclear fusion, where it is encountered during the implosion phase3, and it also represents laboratory analogues of astrophysical environments found in the core of planets and the crusts of old stars4,5. Here we demonstrate how warm dense matter states can be diagnosed and structural properties can be obtained by inelastic X-ray scattering measurements on a compressed lithium sample. Combining experiments and ab initio simulations enables us to determine its microscopic state and to evaluate more approximate theoretical models for the ionic structure.
Similar content being viewed by others
Main
The experimental characterization and theoretical modelling of warm dense matter (WDM) pose severe challenges because WDM spans the intermediate states between solids and plasmas and retains properties common to both. It has moderately-to-strongly coupled but fluid-like ions, which prohibit the exploitation of long-range order as in solids. Expansion techniques used in plasma physics that incorporate correlations perturbatively are also not applicable. From an experimental point of view, the high densities of free electrons make WDM opaque in the visible region and, therefore, usual spectroscopic techniques are not possible. To overcome these limitations, X-ray and proton radiography have been applied to obtain density profiles6,7. Inelastic X-ray scattering has been proposed as an alternative diagnostic method and confirmed to be robust enough to yield density, temperature and ionization state for isochorically heated low-ion-charge (low-Z) matter8,9. Moreover, the equation of state of shocked WDM plastic samples inferred from such measurements has been cross-validated with velocity interferometry measurements10.
Here, we show the results of a new X-ray scattering experiment aimed at the observation of the long-wavelength limit of the ion response in shock-driven matter. In this limit, the system behaves as a single fluid, which can be studied using hydrodynamical laws2. This is also the regime where differences among theoretical models become significant and experimental data are essential to verify the atomic structure and dynamics.
The experimentally measured X-ray scattering cross-section contains information about the microscopic structure of the material because it is directly proportional to the total dynamic structure factor of the scattering electrons:

Here, k=|k0−k1|=(4π/λ0)sin(Θ/2) is the momentum transfer to the photon, k0 and k1 are the wavenumbers of the incident and the scattered photon, respectively, λ0 is the wavelength of the incident X-rays and Θ is the scattering angle; ω=ω0−ω1 is the related energy transfer to or from the photon. For the conditions used here, the average energy transfer to the photon, EC=ℏ2k2/2me (me is the electron mass), is much less than the ionization energy of the K-shell electrons in lithium, and internal excitations can be ignored.
The dynamic structure factor Seetot(k,ω) is a measure for the spatial correlations in the system (unity for uncorrelated systems). The long-range nature of the Coulomb interactions that govern the WDM state gives rise to collective excitations, namely the ion acoustic and the electron plasma modes. These become particularly important in the long-wavelength limit (that is, k→0), and result in peaks in the structure factor. Seetot(k,ω) can be decomposed into two parts that highlight both modes11,

The first term corresponds to the quasi-elastic (Rayleigh) scattering, with Si i(k,ω) being the ion–ion structure factor. fI(k) denotes the atomic/ionic form factor (that is, the density of bound electrons) and q(k) is the density of the electrons in the screening cloud; both terms describe electrons following the ion motion and can be straightforwardly calculated once the electron density and Z are known12. The ion acoustic modes in the ion–ion structure factor are separated by less than 2ℏωpi∼0.2 eV, where ωpi is the ion-plasma frequency. This value is considerably smaller than the bandwidth of the X-ray probe radiation (∼6 eV). Accordingly, we cannot resolve these modes, and treat the ionic correlations as frequency integrated, that is statically: Si i(k,ω)∼Si i(k)δ(ω), with δ(ω) the Dirac delta function. The second term in equation (1) describes the scattering by free electrons that do not follow the ion motion. In the case of collective scattering from Langmuir waves, See0(k,ω) gives rise to a plasmon peak in the scattering spectrum.
Measurement of the spectrally dependent scattering cross-section over a large range of momentum transfers k would enable inference of all plasma parameters and distinguishing between structure models. Owing to the constraints in the target design and laser availability, this is often not possible; in the present work, data have been collected only in the forward scattering direction. A new extended diagnostics approach has been developed that fits the experimental data to equation (1), and applies an equation of state derived from ab initio simulations to obtain a unique set of parameters for WDM with unknown mass density.
Data analysis and experimental results
Warm dense lithium was produced using the Nd:glass Vulcan laser facility at the Rutherford Appleton Laboratory (UK). Laser illumination of a 250 μm thick solid lithium foil (initial density ρ0=0.5 g cm−3) drives a shock wave into the material, thus achieving above-solid-state densities and temperatures of a few electron volts. The X-ray probe is generated approximately ∼3 ns later by focusing the back-lighter beams onto a parylene-D (C8H4Cl2) foil that emits at 2,960 eV (Cl Ly-α line). This radiation is collimated towards the sample (see Fig. 1). The scattered signal is collected under two scattering angles of Θ=40∘ and 60∘ with a cylindrically bent, highly oriented pyrolytic graphite crystal coupled to a CCD (charge coupled device) detector.
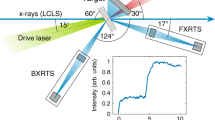
a, Set-up of the experiment, showing the shock-drive and back-lighter beams; the target assembly with a cone shield to avoid undesired signal on the detector, the parylene-D foil, the 170 μm collimating pinhole and the Li target; the line of sight of the flat-field spectrometer and the 60∘ and 40∘ positions for the time-integrated Von Hamos spectrometer. The back-lighter beams are all fired inside the cone shield onto the parylene-D foil, while the drive beams are fired onto the Li sample. b, Time-resolved X-ray pulse profile at 2.96 keV. The initial signal corresponds to the coronal Li plasma emission from the shock-drive beams. The second peak is associated with the X-ray signal from the parylene-D plasma. c, Measured extreme-ultraviolet (space and time integrated) emission spectrum. The background signal is well fitted by a black body with temperature TR∼9±2 eV (see the Methods section).
Figure 2 shows the time-averaged plasma conditions during the duration of the X-ray probe calculated with the radiation hydrodynamic code HELIOS (see the Methods section). The duration of the back-lighter beams (∼1 ns) determines the temporal resolution of the diagnostics. Since the duration of the X-ray pulse follows the duration of the optical pulse (confirmed by X-ray streak measurements), the plasma properties are effectively averaged over 1 ns. Figure 2 indicates slightly compressed lithium with the electron temperature remaining relatively low (Te<10 eV). The extreme-ultraviolet (space- and time-integrated) spectrum measured with a flat-field spectrometer looking edge-on at the sample, from a shot on a free-standing lithium foil, is shown in Fig. 1. In addition to the featureless background emission, carbon lines from the target stalk appear. They are used as wavelength reference. The background signal is well fitted by a black body with temperature TR∼9±2 eV. Since the emergent radiation flux in the transverse (edge-on) direction is dominated by the region of higher density (where the mean opacity is larger), this measurement is consistent with the HELIOS prediction from Fig. 2.
a, Temporal evolution of the plasma conditions inside the Li sample simulated with the one-dimensional radiation hydrodynamics code HELIOS. The region between the white lines defines the interval when the plasma is probed by X-ray scattering. b, Predicted time-averaged Li plasma conditions during the X-ray scattering measurements.
Figure 3 shows the measured experimental spectrum obtained at a scattering angle of Θ=60∘. Compton scattering is significant only for the free electrons, giving rise to an inelastic feature in the spectrum. The position of the inelastic scatter feature is determined by both inelastic momentum transferred from direct Compton (EC∼8.5 eV) and plasma wave scattering (ℏωpe∼10 eV, with ωpe being the electron plasma frequency) and gives the electron density (ne∝Z ρ). The width of the inelastic feature, due to Landau damping, gives Te (ref. 9). The length scale for the microscopic density fluctuations is determined by the screening length (Debye or Thomas–Fermi); for our conditions, this is a small value (<0.1 nm). The macroscopic variations of the system parameters are instead determined by the hydrodynamic motion, with a gradient scale-length (see HELIOS simulations) of a few micrometres. Therefore, the total spectrum is representative of the system parameters averaged over the entire scattering volume.
a, Demonstration of the excellent agreement of the Monte Carlo simulation using the effective ion–ion potential and the full ab initio simulations (DFT-MD). b, Dependence of the fitted values on the mass density and predicted ionization state from ab initio DFT-MD simulations. c, Experimental data at 60∘ scattering angle, showing the elastic peak, from the first term in equation (1), and the inelastic contribution, from the second term in equation (1). This spectrum is fitted using the model discussed in the text, and the best-fit values are density ρ=0.6±0.025 g cm−3, electron temperature Te=4.5±1.5 eV and ion charge Z=1.35±0.1. A synthetic spectrum constructed by postprocessing the hydrodynamic simulation results is also shown. d, χ2 (proportional to the sum of the square difference between the experimental data points and the fit values) plot showing a global minimum in the fitting procedure for Te and Z and the corresponding errors.
The density-weighted, spatially averaged plasma parameters can be obtained by fitting the experimental spectrum with equation (1). If Si i(k;ρ,Z,Te) were known, this could uniquely determine Z and ρ from the intensity ratio between the inelastic and elastic components8. However, the theoretical predictions for the ion–ion structure factor of WDM show a large spread. Leaving Si i(k) as a free parameter strongly reduces the model dependence. However, we now find equally suited fits for different sets of parameters. The complementary information needed to find a unique parameter set is obtained from ab initio simulations using density functional theory (DFT) for all electrons coupled with classical molecular dynamics (MD) for the ions (see the Methods section)13,14,15. These simulations can fully represent the challenges of the WDM state: degenerate electrons and strongly coupled ions. The ionization state is now obtained by matching the pair distribution of DFT-MD and classical Monte Carlo simulations, where the latter uses Z as a free parameter (see the Methods section). The reduction of the numerical noise and the excellent agreement between DFT-MD and Monte Carlo for the ion structure is shown in Fig. 3.
The charge state from the experimental fitting and that extracted from the simulations show opposite trends: whereas the first decreases with increasing mass density the second increases (see Fig. 3). Accordingly, only a unique data set is consistent with both the experimental scattering signal and the ab initio simulation, yielding ρ=0.6±0.025 g cm−3, Te=4.5±1.5 eV and Z=1.35±0.1. The error analysis is based on the standard deviation from the global minimum of the square difference between the experimental data and the fit values (see the χ2 plot of Fig. 3). We notice that both the mass density and the electron temperature are consistent with the hydrodynamic simulation, whereas the ionization degree cannot be expected to be accurate within HELIOS, owing to the nearly ideal equation of state being used (there is a 50% error in the pressure compared with the ab initio simulations, too).
A synthetic spectrum (with Si i left as a fitting parameter) constructed by adding the density-weighted contribution of each numerical cell as extracted from the hydrodynamic simulation is also shown in Fig. 3. This spectrum reproduces the experimental data rather well, with the slight difference in the intensity of the inelastic scatter attributable to an underestimate of the ionization degree. The results of our work represent considerable progress from previous X-ray scattering measurements on compressed samples (see, for example, refs 10, 16), where the mass density was inferred only from the hydrodynamic simulations.
Measurements have been made at two different scattering angles, Θ=40∘ and 60∘, as shown in Fig. 4. Since we have fI(40∘)=1.45±0.1, fI(60∘)=1.43±0.1, and q(40∘)=0.94±0.1, q(60∘)=0.69±0.1, the static structure factors can be easily calculated from the best-fit values. The detector is not absolutely calibrated, thus particle conservation (the f-sum rule) is used to determine the instrument response2

where (d2σ/dΩdω)inel is the measured scattering signal from the free electrons and its integral is given by the shaded area in Fig. 4. The calibration constant C is obtained from the Θ=60∘ measurement. The values obtained for the static ion response are Si i(40∘)=0.64±0.16 and Si i(60∘)=0.71±0.07. We also extracted the ion–ion structure factor directly from the simulations. These however show large fluctuations due to the Fourier transformation of already noisy data. We therefore opt for a more indirect method by extracting the effective ion–ion potentials from DFT-MD (refs 17, 18) and use them in classical Monte Carlo simulations for the structure factors. These prove to be another check of consistency by showing good agreement with the experimental data (see Fig. 5). The same agreement can be achieved with a theoretical model based on a hypernetted chain approach that assumes linearly screened Coulomb interactions between the ions. However, any model that assumes a weak electron–ion pseudo-potential19 or an unscreened one-component plasma model cannot reproduce the data.
a,b, Experimental results at 40∘ (a) and 60∘ (b) scattering angles. For the 60∘ scattering, the transmitted spectrum measured with the flat Si crystal is also shown (see the Methods section). This is representative of the source Cl Ly-α emission. The shaded area under the inelastic scatter feature (b) is used for absolute calibration of the signal using the f-sum rule as discussed in the text. The 40∘-scattering spectrum is fitted with the same plasma parameters as the 60∘ spectrum but with a different value for the ion–ion structure factor, Si i(k).
Experimentally obtained ion–ion structure factors (squares) compared with theoretical predictions for strongly coupled plasmas. Error bars for the 60∘ point have been calculated from the χ2 analysis, whereas the 40∘ point includes uncertainty associated with image-plate fading (see the text and the Methods secton). Monte Carlo simulations used an ion–ion potential extracted from ab initio DFT-MD. HNC calculations used linearly screened and unscreened Coulomb potentials (ultrasoft electron–ion potentials yield structure factors very close to the one-component plasma result—not shown). The green line is a four-component HNC calculation (two ion and two electron species) applying a potential designed to mimic quantum behaviour19.
Methods
Experiment
To generate the X-ray probe radiation, four back-lighter beams from the Vulcan laser20 of ∼100 J (frequency doubled to 527 nm with type-II KDP crystals) in a square 1-ns-long pulse were focused to a ∼100 μm spot onto an 8-μm-thick parylene-D foil, achieving an irradiance of ∼5×1015 W cm−2. The illumination of the parylene-D foil with the back-lighter beams generates emission of Cl Ly-α radiation (at 2,960 eV) with an estimated fluence of ∼1014 photons/sr. In addition, the intensity and spectrum of the radiation transmitted through the lithium was monitored for each shot with a flat Si(111) crystal spectrometer coupled to an image-plate detector21. Due to image-plate fading, different shots are compared by assuming the same detective quantum efficiency, which introduces a ∼17% estimated error. The duration of the X-ray pulse was measured with a X-ray streak camera and found to follow the optical pulse (see Fig. 1).
The target was driven with two 1 ns, ∼20 J (frequency-doubled) beams. A uniform shock wavefront (to avoid collecting radiation scattered from different plasma conditions) was achieved with 400 μm phase zone plates, giving a flat-top focal spot with average irradiance of ∼3×1013 W cm−2.
Time synchronization of the beams was achieved with an optical streak camera with accuracy up to ∼30 ps. A 170 μm Ag pinhole (see Fig. 1) was placed midway between the lithium sample and the parylene-D foil, with a total separation between the lithium sample and the parylene-D foil of 1 mm. This limited the range of probing angles to ±10∘. The highly oriented pyrolytic graphite crystal (in 002 orientation), used in a Von Hamos geometry, was placed 173 mm from the lithium sample and the CCD image plane to take advantage of the mosaic focusing22. The dimensions of the crystal (40×40 mm) gave a high collection angle with an angular resolution of ± 6.6∘.
The flat-field spectrometer23 used to measure the radiation temperature was filtered with 0.3 μm CH and 0.1 μm Al. The shot shown in Fig. 1 was taken with the two drive beams onto a single Li foil.
For each data point, different shots were taken to ensure that the signal was not contaminated by emission other than that from the X-rays scattered from the lithium foil. These ‘null’ shots were performed by removing the Li payload from the target assembly. In addition, shots onto free-standing chlorinated plastic as well as free-standing Li foils were taken for spectral calibration and background correction. The presence of a thin oxide layer (a few micrometres thick) on the surface of the lithium sample has been characterized with electron microscopy. We estimate its overall contribution to the scattering signal as ≲5%.
Hydrodynamic simulations
The one-dimensional radiation hydrodynamics code HELIOS24 uses the PROPACEOUS suite to calculate the lithium equation of state, which has been shown to well agree with the SESAME database. The one-dimensional geometry assumption holds because the laser spot size produced by the phase zone plates has a diameter comparable to the X-ray-scattering-probed region (determined by the pinhole geometry).
Density functional molecular dynamic and Monte Carlo simulations
Density functional molecular dynamic simulations were carried out using the VASP code13,14,15,25. The ions are described by classical MD. Kohn–Sham equations are solved self-consistently for each MD step in the external field of the ions to obtain the instantaneous state of the electrons and thus the forces on the ions (Born–Oppenheimer DFT-MD). To incorporate the effect of temperature on the electrons, the Mermin functional was used26. We explicitly take all three electrons of the lithium atom into account with the projector augmented wave method25,27. The plane-wave basis to represent the electronic wavefunctions had a cut-off of 800 eV. The exchange–correlation contribution was of Perdew–Burke–Ernzerhof type28. Temperature control was established by a Nosé–Hoover thermostat29. The simulations were performed for only the Gamma point with 128 lithium nuclei and 384 electrons for 500–1,000 steps of 0.384 fs. At the experimental temperatures a considerable number of bands had to be taken into account to properly represent all electrons and the tail of the Fermi distribution. Classical Monte Carlo simulations were carried out for systems of up to 1,024 ions interacting via an effective ion–ion potential. The latter was extracted by force matching from the DFT-MD simulation17,18.
Hypernetted chain approach
The hypernetted chain (HNC) approach is a classical integral equation method for strongly coupled fluids30, yielding reasonably accurate equation-of-state and structural information for ions. We used two versions. One treats only the ions (with an average charge state or two ion species with weighted densities), considering the electrons by a screened ion–ion potential. The other version treats the electrons on the same footing (four components: two ion species and two spin species for the electrons)19. In the latter case, quantum effects are modelled approximately by a weak electron–ion pseudo-potential and an additional repulsive exchange potential between like-spin electrons.
References
National Research Council. Frontiers in High Energy Density Physics : The X-Games of Contemporary Science (National Academies Press, 2003).
Ichimaru, S. Strongly coupled plasmas: High-density classical plasmas and degenerate electron liquids. Rev. Mod. Phys. 54, 1017–1059 (1982).
Lindl, J. Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain. Phys. Plasmas 2, 3933–4024 (1995).
Guillot, T. Interiors of giant planets inside and outside the solar system. Science 286, 72–76 (1999).
Vocadlo, L. et al. Possible thermal and chemical stabilization of body-centered-cubic iron in the Earth’s core. Nature 424, 536–539 (2003).
Koenig, M. et al. Progress in the study of warm dense matter. Plasma Phys. Control. Fusion 47, B441–B449 (2005).
Rygg, J. R. et al. Proton radiography of inertial fusion implosions. Science 319, 1223–1225 (2008).
Glenzer, S. H. et al. Demonstration of spectrally resolved x-ray scattering in dense plasmas. Phys. Rev. Lett. 90, 175002 (2003).
Glenzer, S. H. et al. Observations of plasmons in warm dense matter. Phys. Rev. Lett. 98, 065002 (2007).
Ravasio, A. et al. Direct observation of strong ion coupling in laser-driven shock-compressed targets. Phys. Rev. Lett. 99, 135006 (2007).
Chihara, J. Difference in x-ray scattering between metallic and non-metallic liquids due to conduction electrons. J. Phys. Condens. Matter 12, 231–247 (2000).
Gregori, G., Ravasio, A., Höll, A., Glenzer, S. H. & Rose, S. J. Derivation of static structure factor in strongly coupled non-equilibrium plasmas for x-ray scattering studies. High Energy Density Phys. 3, 99–108 (2007).
Kresse, G. & Hafner, J. Ab-initio molecular-dynamics for liquid-metals. Phys. Rev. B 47, RC558–RC561 (1993).
Kresse, G. & Hafner, J. Ab-initio molecular-dynamics simulation of the liquid-metal amorphous–semiconductor transition in germanium. Phys. Rev. B 49, 14251–14269 (1994).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Sawada, H. et al. Diagnosing direct-drive, shock-heated, and compressed plastic planar foils with non-collective spectrally resolved x-ray scattering. Phys. Plasmas 14, 122703 (2007).
Izvekov, S., Parinello, M., Burnham, C. J. & Voth, G. A. Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: A new method for force-matching. J. Chem. Phys. 120, 10896–10913 (2004).
Hone, T. D., Izvekov, S. & Voth, G. A. Fast centroid molecular dynamics: A force-matching approach for the predetermination of the effective centroid forces. J. Chem. Phys. 122, 054105 (2005).
Wünsch, K., Hilse, P., Schlanges, M. & Gericke, D. O. Structure of strongly coupled multicomponent plasmas. Phys. Rev. E. 77, 056404 (2008).
Danson, C. N. et al. Well characterized 1019 W cm−2 operation of VULCAN—an ultra-high power Nd:glass laser. J. Mod. Opt. 45, 1653–1669 (1998).
Paterson, I. J. et al. Image plate response for conditions relevant to laser–plasma interaction experiments. Meas. Sci. Technol. 19, 095301 (2008).
Pak, A. et al. X-ray line measurements with high efficiency Bragg crystals. Rev. Sci. Instrum. 75, 3747–3749 (2004).
Osborn, K. D. & Callcott, T. A. Two new optical designs for soft x-ray spectrometers using variable-linespace gratings. Rev. Sci. Instrum. 66, 3131–3136 (1995).
MacFarlane, J. J. et al. HELIOS-CR—A 1D radiation-magnetohydrodynamics code with inline atomic kinetics modeling. J. Quant. Spectrosc. Radiat. Transfer 99, 381–397 (2006).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Mermin, N. D. Thermal properties of the inhomogeneous electron gas. Phys. Rev. 137, A1441–A1443 (1965).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Hoover, W. G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697 (1985).
Van Leuwen, J. M. J., Groenveld, J. & DeBoer, J. New method for the calculation of the pair correlation function. Physica 25, 792–808 (1959).
Acknowledgements
This work was partially supported by EPSRC grants and by the Science and Technology Facilities Council of the United Kingdom. Additional support from the US DOE and the Lawrence Livermore National Laboratory is also acknowledged. We thank the Vulcan operation, engineering and target fabrication groups for their support during the experiment.
Author information
Authors and Affiliations
Contributions
E.G.S., G.G., B.B., R.J.C., F.Y.K., M.M.N., A.P., R.L.W. and D.R. carried out the Vulcan experiment. E.G.S., G.G., S.H.G., P.N., A.P., D.P., M.R. and M.S. carried out preparatory experiments and diagnostics development at the Lawrence Livermore National Laboratory. E.G.S., G.G., F.Y.K. and D.R. analysed the data. E.G.S., G.G. and D.O.G. wrote the paper. The simulations were carried out by D.O.G., J.V. and K.W. C.S. and G.G. designed targets used in the experiment. R.R.F., S.H.G., M.K., O.L.L., D.N., M.R. and L.v.W. provided additional experimental and theoretical support. G.G., S.H.G. and D.R. conceived the project in this paper.
Corresponding author
Rights and permissions
About this article
Cite this article
García Saiz, E., Gregori, G., Gericke, D. et al. Probing warm dense lithium by inelastic X-ray scattering. Nature Phys 4, 940–944 (2008). https://doi.org/10.1038/nphys1103
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1103
This article is cited by
-
A strong diffusive ion mode in dense ionized matter predicted by Langevin dynamics
Nature Communications (2017)
-
Theory of Thomson scattering in inhomogeneous media
Scientific Reports (2016)
-
X-ray scattering measurements of dissociation-induced metallization of dynamically compressed deuterium
Nature Communications (2016)
-
Linear dependence of surface expansion speed on initial plasma temperature in warm dense matter
Scientific Reports (2016)
-
Observation of finite-wavelength screening in high-energy-density matter
Nature Communications (2015)