Abstract
Einstein’s 1925 paper predicted the occurrence of Bose–Einstein condensation (BEC) in an ideal gas of non-interacting bosonic particles1. However, particle–particle interaction and peculiar excitation spectra are keys for understanding BEC and superfluidity physics. A quantum field-theoretical formulation for a weakly interacting Bose condensed system was developed by Bogoliubov in 1947, which predicted the phonon-like excitation spectrum2 in the low-momentum regime. The experimental verification of the Bogoliubov theory on the quantitative level was carried out for atomic BEC3 using the two-photon Bragg scattering technique4. Exciton-polaritons in a semiconductor microcavity, which are elementary excitations created by strong coupling between quantum-well excitons and microcavity photons, were proposed as a new BEC candidate in solid-state systems5. Recent experiments with exciton-polaritons have demonstrated several interesting signatures from the viewpoint of polariton condensation, such as quantum degeneracy at non-equilibrium conditions6,7,8, the polariton-bunching effect at the condensation threshold9, long spatial coherence10,11,12 and quantum degeneracy at equilibrium conditions13. The particle–particle interaction and the Bogoliubov excitation spectrum are at the heart of BEC and superfluidity physics, but have only been studied theoretically for exciton-polaritons14,15. In this letter, we report the first observation of interaction effects on the exciton-polariton condensate and the excitation spectra, which are in quantitative agreement with the Bogoliubov theory.
Similar content being viewed by others
Main
In a semiconductor microcavity with single or multiple quantum wells (QWs), eigenstates are altered to the new normal modes, called exciton-polaritons, when the cavity photon/QW-exciton coupling rate exceeds the decay rates of the photon and exciton. The exciton-polariton is a promising solid-state system for studying the dynamical condensation phenomena in solids5,16. Because its effective mass is eight orders of magnitude smaller than that of a hydrogen atom and four orders of magnitude smaller than exciton mass, the critical temperature of the polariton Bose–Einstein condensation (BEC) transition is expected to be up to room temperature. The leakage photons carry identical energy and in-plane momentum to the internal polaritons, thus it is possible to directly measure the energy–momentum dispersion relation and population distribution of the polaritons by an angle-resolved spectroscopy technique. This important information is available for liquid-4He systems only through ‘quantum evaporation’17 and for gaseous atoms only through ‘Feshbach resonance controlled free expansion’.
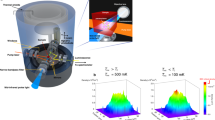
The exciton-polariton trap used in our experiment is shown in Fig. 1a. Three stacks of four GaAs QWs are embedded at the central three antinode positions of an AlAs/AlGaAs distributed Bragg reflector planar microcavity. The normal-mode splitting is 2g0∼15 meV and the cavity photon lifetime is 2 ps. This leads to a k=0 lower-polariton (LP) lifetime of ∼4 ps at zero detuning, Δ≡EC−EX=0, where k is the in-plane wavenumber and EC and EX are the cavity and QW exciton energies at k=0. The trap potential of ∼200 μeV is provided by a hole surrounded by a thin metal (Ti/Au) film18. The cavity resonant field normally has an antinode at the AlGaAs–air interface. However, the antinode position is shifted inside the AlGaAs layer with the metal film as shown in Fig. 1a, which results in a blueshift of the cavity resonance and the LP energy. In our experiment, the LPs were confined in circular holes of varying diameters from 5 μm to 100 μm. In a trap with 5–10 μm diameter, a single fundamental transverse mode dominates the condensation dynamics over other higher-order modes owing to the relatively weak confining potential.
a, A schematic diagram of a polariton trap formed by a thin metal film (Ti/Au: 4/20 nm) on top of a microcavity structure with circular holes (diameter:4–100 μm). The microcavity consists of a λ/2 AlAs optical cavity layer sandwiched by two distributed Bragg reflectors with alternating AlGaAs/AlAs λ/4 layers, where λ is the cavity resonance wavelength. Three stacks of four GaAs QWs are placed at the central three antinodes of the microcavity photon field. A photon-field amplitude has an antinode at an AlGaAs–air interface without a metal film, whereas a deposited thin metal film pushes an antinode position inside the AlGaAs layer, which results in the blueshift of the cavity resonance and the lower polariton (LP) energy. The blueshift of the LP energy under the metal film is typically ∼200 μeV. b, The total number n of LPs injected into a trap (pink dashed line) and number n0 of the LP centred at k=0 and within  (red circles), which approximately corresponds to the LP number of the ground state of the trap, are plotted as functions of P/Pth. Inset: The fractional population n0/n as a function of P/Pth. The linearly polarized laser beam is injected with an angle of 60∘ (k=7×104 cm−1) into a trap with 8 μm diameter, where the detuning parameter is Δ=5.4 meV. c, The measured standard deviations of LP distribution in coordinate Δx (blue circles) and in wavenumber Δk (red crosses) are plotted as a function of P/Pth. Theoretical values for Δx and Δk obtained by the GP equation are shown by blue and red solid lines (Supplementary Information, S1). Top panels are the near-field images at three different pump levels: 0.3Pth, Pth and 2.5Pth. d, The measured LP energy shift at k=0 (blue diamonds) and energy shift U(n) calculated by equation (1) (light-blue solid line) are plotted as functions of the total number of polaritons. The numerical results by the GP equation, including the effect of pump-dependent condensate size, are shown by red circles (Supplementary Information, S1).
(red circles), which approximately corresponds to the LP number of the ground state of the trap, are plotted as functions of P/Pth. Inset: The fractional population n0/n as a function of P/Pth. The linearly polarized laser beam is injected with an angle of 60∘ (k=7×104 cm−1) into a trap with 8 μm diameter, where the detuning parameter is Δ=5.4 meV. c, The measured standard deviations of LP distribution in coordinate Δx (blue circles) and in wavenumber Δk (red crosses) are plotted as a function of P/Pth. Theoretical values for Δx and Δk obtained by the GP equation are shown by blue and red solid lines (Supplementary Information, S1). Top panels are the near-field images at three different pump levels: 0.3Pth, Pth and 2.5Pth. d, The measured LP energy shift at k=0 (blue diamonds) and energy shift U(n) calculated by equation (1) (light-blue solid line) are plotted as functions of the total number of polaritons. The numerical results by the GP equation, including the effect of pump-dependent condensate size, are shown by red circles (Supplementary Information, S1).
The total number n of LPs injected into a trap by the pump pulse and the number n0 of the LP centred at k=0 and within  , corresponding approximately to the trapped ground state, are plotted in Fig. 1b as a function of normalized pump rate P/Pth. The fractional ratio n0/n increases nonlinearly at the condensation threshold and reaches a maximum of ∼0.6 at P/Pth∼6.
, corresponding approximately to the trapped ground state, are plotted in Fig. 1b as a function of normalized pump rate P/Pth. The fractional ratio n0/n increases nonlinearly at the condensation threshold and reaches a maximum of ∼0.6 at P/Pth∼6.
The top panels in Fig. 1c show the near-field emission patterns from a trap with 8 μm diameter at pump rates below, just above and well above the condensation threshold. The measured standard deviations for the polariton position Δx and the wavenumber Δk are plotted as functions of P/Pth in Fig. 1c. Sudden decreases in Δx and Δk were clearly observed at  . Just above threshold, the measured uncertainty product ΔxΔk is ∼0.98, which may be compared to the Heisenberg limit (ΔxΔk∼0.5) for a minimum-uncertainty wavepacket. The monotonic increase in Δx and ΔxΔk at higher pump rates stems from the repulsive interaction among LPs in a condensate and is well reproduced by theoretical analysis using the Gross–Pitaevskii (GP) equation as shown in Fig. 1c (Supplementary Information, S1 for detailed theoretical analysis and Supplementary Information, S2 for complete experimental data.)
. Just above threshold, the measured uncertainty product ΔxΔk is ∼0.98, which may be compared to the Heisenberg limit (ΔxΔk∼0.5) for a minimum-uncertainty wavepacket. The monotonic increase in Δx and ΔxΔk at higher pump rates stems from the repulsive interaction among LPs in a condensate and is well reproduced by theoretical analysis using the Gross–Pitaevskii (GP) equation as shown in Fig. 1c (Supplementary Information, S1 for detailed theoretical analysis and Supplementary Information, S2 for complete experimental data.)
The k=0 LP energy is blueshifted with the number of polaritons as shown in Fig. 1d. This is a direct manifestation of the aforementioned repulsive interaction among LPs in a condensate. The k=0 LP energy shift U(n) is calculated by the relation

where δ EX=EB(n/ns) and g(n)=g0(1−(n/ns′)) represent the blueshift of the QW exciton energy due to fermionic exchange interaction19,20 and the reduced normal-mode splitting due to phase-space filling and fermionic exchange interaction21, respectively. ns=(NQWS/2.2πaB*2|X|2) and ns′=(NQWS/4πaB*2|X|2) are the saturation polariton numbers for the above two nonlinear processes, respectively. aB* is the QW exciton Bohr radius, NQW=12 is the number of QWs, g0≈7.5 meV is the photon–exciton coupling strength, S is the cross-sectional area of the condensate and  is the exciton fraction of the k=0 LP.
is the exciton fraction of the k=0 LP.
If we ignore the pump-rate dependency of the condensate cross-sectional area and assume a constant cross-sectional area determined by the trap area S=π(4×10−4 cm)2, the theoretical energy shift is shown by the light-blue line in Fig. 1d. We can numerically solve the GP equation to incorporate the pump-rate-dependent condensate size (see Supplementary Information, S1). The results are shown by red circles in Fig. 1d. These two theoretical predictions are compared with the experimental results (blue diamonds). We note that the above-mentioned nonlinear model based on weakly interacting bosons19,20,21 can reproduce the experimental data only in low-polariton-density regimes. Therefore, we use the experimental values (not theoretical values) for U(n) as the interaction energy in subsequent discussions for the universal feature of the Bogoliubov excitations.
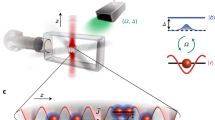
The dispersion relations between the LP energy E and in-plane wavenumber k obtained by the angle-resolved spectroscopy are shown for the pump rate above threshold P/Pth=3 in Fig. 2. Figure 2a represents a linear plot of the intensity, whereas Fig. 2b–d use logarithmic plots of the intensity to magnify the excitation spectra. Here we show an ‘untrapped’ case, where the pump spot size (diameter ∼30 μm) is considerably smaller than the trap size (diameter∼90 μm). In such a case, the LP condensate is formed in an area determined by the pump spot size and the pump rate rather than the trap size owing to the limited lateral diffusion and varying spatial density of the LPs12,18. Above threshold, two drastic changes are noticed compared with the standard quadratic dispersion observed far below threshold. One is the blueshift of the k=0 LP energy and the other is the phonon-like linear dispersion relation in the low-momentum regime |k ξ|<1, where  is the healing length. White and black lines in Fig. 2b represent the two quadratic dispersion relations, ELP=−U(n)+((ℏk)2/2m) and ELP′=((ℏk)2/2m), where m is the effective mass of the k=0 LP. Here we choose the zero energy as the condensate energy for convenience. Neither of the two theoretical curves can explain the measurement result. A solid pink line in Fig. 2b is the Bogoliubov excitation energy, given by22,23
is the healing length. White and black lines in Fig. 2b represent the two quadratic dispersion relations, ELP=−U(n)+((ℏk)2/2m) and ELP′=((ℏk)2/2m), where m is the effective mass of the k=0 LP. Here we choose the zero energy as the condensate energy for convenience. Neither of the two theoretical curves can explain the measurement result. A solid pink line in Fig. 2b is the Bogoliubov excitation energy, given by22,23

The measured dispersion relation for the excitation energy versus in-plane wavenumber is in good agreement with the Bogoliubov excitation spectrum without any fitting parameter.
a, A linear plot of the intensity; b–d three-dimensional logarithmic plots of the intensity to magnify the excitation spectra. Time-integrated dispersion relation between the LP energy (in the range of 8 meV centred at 1.609 eV) versus in-plane wavenumber for the untrapped condensate system, where the detuning parameter is Δ=1.4 meV and the pump rate is P=3Pth (Pth=17 mW). A circularly polarized pump beam was incident with an angle of 60∘. Three detection schemes: detection of the leakage photons with the cocircular polarization as the pump beam (a,b), detection of the cross-circular polarization (c) and detection of a small amount of mixture of the cocircular polarization with the cross-circular polarization (d). The theoretical curves represent the Bogoliubov excitation energy EB (pink line), the quadratic dispersion relations ELP′ (black line), which start from the condensate energy, and the non-interacting free-polariton dispersion relation ELP (white line), which is experimentally determined by the data taken far below the threshold P=0.001Pth.
A circularly polarized pump laser beam was used to inject spin-polarized LPs in this experiment. In such a case, the LP condensate preserves the original spin polarization of optically injected polaritons24. The result shown in Fig. 2b was taken for detecting the leakage photons with the same circular polarization as that of the pump (cocircular detection). If leakage photons with cross-circular polarization were detected, the standard quadratic dispersion was obtained but with slightly blueshifted energy, as shown in Fig. 2c. Even though the circularly polarized pump beam is injected, a small number of cross-circularly polarized photons was detected because of the spin-flip relaxation during a cooling process24. On increasing the pump rate, the number of LPs with opposite spin is also increased, so their energy is blueshifted compared with the single-polariton energy ELP (white line) in Fig. 2c. In Fig. 2d we intentionally mixed a small number of the cocircular polarized photons to be detected with the cross-circular polarized photons. The difference between the Bogoliubov excitations with cocircular polarization and the standard quadratic excitation with cross-circular polarization is clearly seen.
The dispersion curves for the LP condensate in a trap with 8 μm diameter are shown in Fig. 3 for below and above threshold. The increasing blueshift of the condensate energy with the pump rate is seen from Fig. 3b to d. The Bogoliubov excitation energy is modified if the density of a condensate is not homogeneous in space owing to trapping in a finite size25. The light-blue dotted line in Fig. 3b is the modified Bogoliubov excitation energy based on the local density-dependent excitation energy  and the spatial average of EB(r), where U(n) varies with position (Supplementary Information, S3). In the phonon-like regime (|k ξ|<1), the Bogoliubov dispersion is still linear, E≈C′k. However, the speed of sound is not equal to
and the spatial average of EB(r), where U(n) varies with position (Supplementary Information, S3). In the phonon-like regime (|k ξ|<1), the Bogoliubov dispersion is still linear, E≈C′k. However, the speed of sound is not equal to  as in the homogeneous case, but is slightly reduced. In the free-particle regime (|k ξ|>1), the dispersion is still quadratic, EB(|k ξ|>1)≈U′(n)+((ℏk)2/2m). Here, the off-set energy U′(n) is also given by the spatial average of U(n). Just above threshold, the experimental result agrees with such an inhomogeneous model (light-blue dotted line) rather than a homogeneous model (pink solid line). However, as shown in Fig. 3c,d, the excitation spectra of the trapped condensates well above threshold are well reproduced by the homogeneous model. According to the local density approximation, at relatively high pump rates, the trapped condensate spreads over the entire trap owing to the repulsive interaction among condensate polaritons and thus interacts with the excitations uniformly. Such a system can be well described by the homogeneous model (Supplementary Information, S3).
as in the homogeneous case, but is slightly reduced. In the free-particle regime (|k ξ|>1), the dispersion is still quadratic, EB(|k ξ|>1)≈U′(n)+((ℏk)2/2m). Here, the off-set energy U′(n) is also given by the spatial average of U(n). Just above threshold, the experimental result agrees with such an inhomogeneous model (light-blue dotted line) rather than a homogeneous model (pink solid line). However, as shown in Fig. 3c,d, the excitation spectra of the trapped condensates well above threshold are well reproduced by the homogeneous model. According to the local density approximation, at relatively high pump rates, the trapped condensate spreads over the entire trap owing to the repulsive interaction among condensate polaritons and thus interacts with the excitations uniformly. Such a system can be well described by the homogeneous model (Supplementary Information, S3).
a–d, Time-integrated dispersion relations between the LP energy (in the range of 8 meV centred at 1.61 eV) versus in-plane wavenumber. The circularly polarized pump beam is injected into a trap with 8 μm diameter, where the detuning parameter is Δ=1.6 meV. Pump rates are P=0.05Pth (a), P=1.2Pth (b), P=4Pth (c) and P=6Pth (d), where Pth=4 mW. Three theoretical curves represent the Bogoliubov excitation energy EB on the basis of the homogeneous model (pink line), the quadratic dispersion curve E′LP starting from the condensate energy (black line) and the non-interacting free-polariton quadratic dispersion curve ELP (white line) that is determined by the experimental data shown in a. In b the light-blue dotted line shows the Bogoliubov excitation curve based on the local-density approximation (Supplementary Information, S3).
As indicated by equation (2), the Bogoliubov excitation energy normalized by the interaction energy EB/U(n) is a universal function of the wavenumber normalized by the healing length k ξ. In Fig. 4a, this universal relation (green solid line) is compared with the experimental results for four different untrapped condensate systems. The experimental data shown in Fig. 4a are taken by numerical search for the intensity maximum wavenumber for varying E values. In both the phonon-like regime at |k ξ|<1 and the free-particle regime at |k ξ|>1, the experimental results agree well with the universal curve. On the other hand, at a pump rate far below threshold, the measured dispersion relation is completely described by the single-polariton energy ELP (red solid line).
a, Numerically searched excitation energy normalized by the interaction energy E/U(n) as a function of normalized wavenumber k ξ for four different untrapped condensate systems. A, Δ=1.41 meV, P=4Pth (Pth=6.3 mW); B, Δ=0.82 meV, P=8Pth (Pth=8.2 mW); C, Δ=4.2 meV, P=4Pth (Pth=6.4 mW); D, Δ=−0.23 meV, P=24Pth (Pth=8.2 mW). The experimental data far below threshold are also plotted by blue crosses for system A. Three theoretical dispersion curves normalized by the interaction energy are plotted: the Bogoliubov excitation energy EB/U(n) starting from the condensate energy (green solid line), the quadratic dispersion curves E′LP/U(n) (grey solid line) and the free-polariton dispersion ELP/U(n) (red solid line). b,c, The energy shift EB−ELP in the free-particle regime (|k ξ|=1) is plotted as a function of the interaction energy U(n) for the same four different untrapped systems as in a (b) and for four different trapped systems (c), where trapped condensate systems are labelled as follows: E, d(diameter)=7 μm, Δ=3.3 meV; F, d=7 μm, Δ=2.9 meV; G, d=8 μm, Δ=1.6 meV; H, d=8 μm, Δ=2.5 meV. The dashed line represents the theoretical prediction on the basis of the homogeneous model EB−ELP=2U(n). d, LP population distribution normalized by the value at k ξ=0.5 for the trapped system G (in c) at the pump rate P=2Pth (Pth=4 mW). The theoretical 1/k2 dependency for the thermal depletion is shown by the blue solid line. The experimental data are plotted in the range of k ξ=0.2–0.6 because the experimental data at |k ξ|<0.2 are dominated by the condensate with a finite Δk and the Bogoliubov excitation is suppressed (see Supplementary Information, S3).
The sound velocity deduced from the phonon-like linear dispersion spectrum is of the order of ∼108 cm s−1. This value is eight orders of magnitude larger than that of atomic BEC. This enormous difference comes from the fact that the polariton mass is eight orders of magnitude smaller than the atomic mass and the polariton interaction energy is seven orders of magnitude larger than the atomic interaction energy. According to the Landau criterion26, the observation of this linear dispersion in the low-momentum regime is an indication of superfluidity in the exciton-polariton system. However, we note that a polariton system is a dynamical system with a finite lifetime, so the Landau criterion might be modified on a quantitative level.
In the free-particle regime (|k ξ|>1), the excitation energy associated with the condensate is larger by 2U(n) than that of a single LP for the same wavenumber. In Fig. 4b,c, this important prediction of the Bogoliubov theory is compared with the experimental results for four different untrapped and trapped condensate systems, respectively. The experimental data were determined as the difference between the measured excitation energy with the presence of the condensate and the standard quadratic dispersion for a single LP state, which is determined by the experimental data obtained for a pump rate far below threshold (P/Pth≪1). The experimental data were taken for varying pump rates in the range of P/Pth≫1 so that the homogeneous model can be applied to both untrapped and trapped cases. The experimental data are in good agreement with the theoretical curve (grey dashed line) for both untrapped and trapped cases.
Figure 4d shows the normalized LP number nk/nk0 versus the normalized wavenumber |k ξ| for a trapped condensate, where nk0 is evaluated at |k ξ|=0.5 for convenience. The LP occupation number nk in the excitation spectrum can be calculated by applying the Bose–Einstein distribution for the Bogoliubov quasiparticles and subsequently taking the inverse Bogoliubov transformation22,


The first and second terms of the right-hand side of equation (3) represent the real particles (exciton-polaritons) created by the quantum depletion and the thermal depletion, respectively. In the present polariton condensate system, the thermal depletion is much stronger than the quantum depletion, so the second term of the right-hand side of equation (3) dominates over the first term (Supplementary Information, S4). In such a case, the LP population is approximated by nk≈(m kBT/(ℏk)2) in the small-|k ξ| regime, whereas the LP population is given by  if the quantum depletion is dominant22. This theoretical prediction of 1/k2 dependency of nk for thermal depletion is compared with the experimental data in Fig. 4d and reasonable agreement was obtained.
if the quantum depletion is dominant22. This theoretical prediction of 1/k2 dependency of nk for thermal depletion is compared with the experimental data in Fig. 4d and reasonable agreement was obtained.
References
Einstein, A. Quantentheorie des einatomigen idealen Gases: Zweite Abhandlung. Sitzungber. Preuss. Akad. Wiss. 1, 3–14 (1925).
Bogoliubov, N. N. On the theory of superfluidity. J. Phys. USSR 11, 23–32 (1947).
Anderson, M. H. et al. Observation of Bose–Einstein condensation in a dilute atomic vapor. Science 269, 198–201 (1995).
Stamper-Kurn, D. M. et al. Excitation of phonons in a Bose–Einstein condensate by light scattering. Phys. Rev. Lett. 83, 2876–2879 (1999).
Imamoglu, A., Ram, R. J., Pau, S. & Yamamoto, Y. Nonequilibrium condensates and lasers without inversion: Exciton-polariton lasers. Phys. Rev. A 53, 4250–4253 (1996).
Dang, L. S. et al. Stimulation of polariton photoluminescence in semiconductor microcavity. Phys. Rev. Lett. 81, 3920–3923 (1998).
Senellart, P. & Bloch, J. Nonlinear emission of microcavity polaritons in the low density regime. Phys. Rev. Lett. 82, 1233–1236 (1999).
Savvidis, P. G. et al. Angle-resonant stimulated polariton amplifier. Phys. Rev. Lett. 84, 1547–1550 (2000).
Deng, H. et al. Condensation of semiconductor microcavity exciton polaritons. Science 298, 199–202 (2002).
Kasprzak, J. et al. Bose–Einstein condensation of exciton polaritons. Nature 443, 409–414 (2006).
Balili, R. et al. Bose–Einstein condensation of microcavity polaritons in a trap. Science 316, 1007–1010 (2007).
Deng, H. et al. Spatial coherence of a polariton condensate. Phys. Rev. Lett. 99, 126403 (2007).
Deng, H. et al. Quantum degenerate exciton-polaritons in thermal equilibrium. Phys. Rev. Lett. 97, 146402 (2006).
Sarchi, D. & Savona, V. Spectrum and thermal fluctuations of a microcavity polariton Bose–Einstein condensate. Phys. Rev. B 77, 045304 (2008).
Shelykh, I. A., Malpuech, G. & Kavokin, A. V. Bogoliubov theory of Bose-condensates of spinor exciton-polaritons. Phys. Status Solidi A 202, 2614–2620 (2005).
Keeling, J., Marchetti, F. M., Szymanska, M. H. & Littlewood, P. B. Collective coherence in planar semiconductor microcavities. Semicond. Sci. Technol. 22, R1–R26 (2007).
Wyatt, A. F. G. Evidence for a Bose–Einstein condensate in liquid 4He from quantum evaporation. Nature 391, 56–59 (1997).
Lai, C.W. et al. Coherent zero-state and π-state in an exciton-polariton condensate array. Nature 450, 529–532 (2007).
Ciuti, C. et al. Role of the exchange of carriers in elastic exciton–exciton scattering in quantum wells. Phys. Rev. B 58, 7926–7933 (1998).
Rochat, G. et al. Excitonic Bloch equations for a two-dimensional system of interacting excitons. Phys. Rev. B 61, 13856–13862 (2000).
Schmitt-Rink, S., Chemla, D. S. & Miller, D. A. B. Theory of transient excitonic optical nonlinearities in semiconductor quantum-well structures. Phys. Rev. B 32, 6601–6609 (1985).
Pitaevskii, L. P. & Stringari, S. Bose–Einstein Condensation (Clarendon, Oxford, 2003).
Ozeri, R., Katz, N., Steinhauer, J. & Davidson, N. Colloquium: Bulk Bogoliubov excitations in a Bose–Einstein condensate. Rev. Mod. Phys. 77, 187–205 (2005).
Deng, H. et al. Polariton lasing versus photon lasing in a semiconductor microcavity. Proc. Natl Acad. Sci. USA 100, 15318–15323 (2003).
Stenger, J. et al. Bragg spectroscopy of a Bose–Einstein condensate. Phys. Rev. Lett. 82, 4569–4573 (1999).
Landau, L. D. & Lifshiëtís, E. M. Fluid Mechanics 2nd edn (Pergamon, Oxford, 1987).
Acknowledgements
This work was supported by the JST/SORST programme and Special Coordination Funds for Promoting Science and Technology in Japan. We thank T. Maruyama for support and S. Sasaki for device fabrication.
Author information
Authors and Affiliations
Contributions
S.U. carried out the experiments, analysed the data and wrote the paper, L.T. theoretically studied the data, G.R. carried out the experiments and analysed the data, C.W.L. conceived, designed and carried out the experiments, N.K., T.F., M.G., A.L., S.H. and A.F. prepared materials and experimental tools and Y.Y. conceived the project in this paper.
Corresponding authors
Supplementary information
Supplementary Information
Supplementary Information and Supplementary Figures 1—9 (PDF 432 kb)
Rights and permissions
About this article
Cite this article
Utsunomiya, S., Tian, L., Roumpos, G. et al. Observation of Bogoliubov excitations in exciton-polariton condensates. Nature Phys 4, 700–705 (2008). https://doi.org/10.1038/nphys1034
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1034
This article is cited by
-
Ultrafast imaging of polariton propagation and interactions
Nature Communications (2023)
-
Collective excitations of a bound-in-the-continuum condensate
Nature Communications (2023)
-
Non-equilibrium Bose–Einstein condensation in photonic systems
Nature Reviews Physics (2022)
-
Directional Goldstone waves in polariton condensates close to equilibrium
Nature Communications (2020)
-
Observation of quantum depletion in a non-equilibrium exciton–polariton condensate
Nature Communications (2020)