Abstract
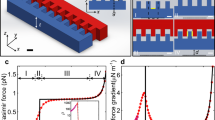
Casimir forces are of fundamental interest because they originate from quantum fluctuations of the electromagnetic field1. Apart from controlling this force via the optical properties of materials2,3,4,5,6,7,8,9,10,11, a number of novel geometries have been proposed to generate repulsive and/or non-monotonic Casimir forces between bodies separated by vacuum gaps12,13,14. Experimental realization of these geometries, however, is hindered by the difficulties in alignment when the bodies are brought into close proximity. Here, using an on-chip platform with integrated force sensors and actuators15, we circumvent the alignment problem and measure the Casimir force between two surfaces with nanoscale protrusions. We demonstrate that the force depends non-monotonically on the displacement. At some displacements, the Casimir force leads to an effective stiffening of the nanomechanical spring. Our findings pave the way for exploiting the Casimir force in nanomechanical systems using structures of complex and non-conventional shapes.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Casimir, H. B. G. On the attraction between two perfectly conducting plates. Proc. Kon. Ned. Akad. Wet. 51, 793–795 (1948).
Derjaguin, B. V., Abrikosova, I. I. & Lifshitz, E. M. Direct measurement of molecular attraction between solids separated by a narrow gap. Q. Rev. Chem. Soc. 10, 295–329 (1956).
Lamoreaux, S. K. Demonstration of the Casimir force in the 0.6 to 6 μm range. Phys. Rev. Lett. 78, 5–8 (1997).
Decca, R. S., López, D., Fischbach, E. & Krause, D. E. Measurement of the Casimir force between dissimilar metals. Phys. Rev. Lett. 91, 050402 (2003).
Chen, F., Klimchitskaya, G. L., Mostepanenko, V. M. & Mohideen, U. Control of the Casimir force by the modification of dielectric properties with light. Phys. Rev. B 76, 035338 (2007).
Munday, J. N., Capasso, F. & Parsegian, V. A. Measured long-range repulsive Casimir–Lifshitz forces. Nature 457, 170–173 (2009).
de Man, S., Heeck, K., Wijngaarden, R. J. & Iannuzzi, D. Halving the Casimir force with conductive oxides. Phys. Rev. Lett. 103, 040402 (2009).
Torricelli, G. et al. Switching Casimir forces with phase-change materials. Phys. Rev. A 82, 010101 (2010).
Sushkov, A. O., Kim, W. J., Dalvit, D. A. R. & Lamoreaux, S. K. Observation of the thermal Casimir force. Nat. Phys. 7, 230–233 (2011).
Laurent, J., Sellier, H., Mosset, A., Huant, S. & Chevrier, J . Casimir force measurements in Au–Au and Au–Si cavities at low temperature. Phys. Rev. B 85, 035426 (2012).
Garcia-Sanchez, D., Fong, K. Y., Bhaskaran, H., Lamoreaux, S. & Tang, H. X. Casimir force and in situ surface potential measurements on nanomembranes. Phys. Rev. Lett. 109, 027202 (2012).
Rodriguez, A. W., Joannopoulos, J. D. & Johnson, S. G. Repulsive and attractive Casimir forces in a glide-symmetric geometry. Phys. Rev. A 77, 062107 (2008).
Levin, M., McCauley, A. P., Rodriguez, A. W., Reid, M. T. H. & Johnson, S. G . Casimir repulsion between metallic objects in vacuum. Phys. Rev. Lett. 105, 090403 (2010).
Rodriguez, A. W., Capasso, F. & Johnson, S. G. The Casimir effect in microstructured geometries. Nat. Photon. 5, 211–221 (2011).
Zou, J. et al. Casimir forces on a silicon micromechanical chip. Nat. Commun. 4, 1845 (2013).
Serry, F. M., Walliser, D. & Maclay, G. J. The role of the Casimir effect in the static deflection and stiction of membrane strips in microelectromechanical systems (MEMS). J. Appl. Phys. 84, 2501–2506 (1998).
Buks, E. & Roukes, M. L. Stiction, adhesion energy, and the Casimir effect in micromechanical systems. Phys. Rev. B 63, 033402 (2001).
Bressi, G., Carugno, G., Onofrio, R. & Ruoso, G. Measurement of the Casimir force between parallel metallic surfaces. Phys. Rev. Lett. 88, 041804 (2002).
Chan, H. B. et al. Measurement of the Casimir force between a gold sphere and a silicon surface with nanoscale trench arrays. Phys. Rev. Lett. 101, 030401 (2008).
Intravaia, F. et al. Strong Casimir force reduction through metallic surface nanostructuring. Nat. Commun. 4, 2515 (2013).
Chiu, H. C., Klimchitskaya, G. L., Marachevsky, V. N., Mostepanenko, V. M. & Mohideen, U. Lateral Casimir force between sinusoidally corrugated surfaces: asymmetric profiles, deviations from the proximity force approximation, and comparison with exact theory. Phys. Rev. B 81, 115417 (2010).
Reid, M. T. H., Rodriguez, A. W., White, J. & Johnson, S. G. Efficient computation of Casimir interactions between arbitrary 3D objects. Phys. Rev. Lett. 103, 040401 (2009).
Davids, P. S., Intravaia, F., Rosa, F. S. S. & Dalvit, D. A. R. Modal approach to Casimir forces in periodic structures. Phys. Rev. A 82, 062111 (2010).
Messina, R. & Antezza, M. Scattering-matrix approach to Casimir–Lifshitz force and heat transfer out of thermal equilibrium between arbitrary bodies. Phys. Rev. A 84, 042102 (2011).
Lussange, J., Guérout, R. & Lambrecht, A. Casimir energy between nanostructured gratings of arbitrary periodic profile. Phys. Rev. A 86, 062502 (2012).
Krüger, M., Emig, T. & Kardar, M. Nonequilibrium electromagnetic fluctuations: heat transfer and interactions. Phys. Rev. Lett. 106, 210404 (2011).
Milton, K. A. et al. Repulsive Casimir effects. Int. J. Mod. Phys. A 27, 1260014 (2012).
Homer Reid, M. T. & Johnson, S. G. Efficient computation of power, force, and torque in BEM scattering calculations. Preprint at https://arxiv.org/abs/1307.2966 (2013).
Eichenfield, M., Camacho, R., Chan, J., Vahala, K. J. & Painter, O. A picogram- and nanometre-scale photonic-crystal optomechanical cavity. Nature 459, 550–555 (2009).
Rahi, S. J., Kardar, M. & Emig, T. Constraints on stable equilibria with fluctuation-induced (Casimir) forces. Phys. Rev. Lett. 105, 070404 (2010).
Lambrecht, A., Pirozhenko, I., Duraffourg, L. & Andreucci, P. The Casimir effect for silicon and gold slabs. Europhys. Lett. 77, 44006 (2007).
Chen, F., Mohideen, U., Klimchitskaya, G. L. & Mostepanenko, V. M. Experimental test for the conductivity properties from the Casimir force between metal and semiconductor. Phys. Rev. A 74, 022103 (2006).
Pierret, R. F. Semiconductor Fundamentals (Addison-Wesley, 1988).
Acknowledgements
H.B.C., L.T. and M.W. are supported by HKUST 16300414 from the Research Grants Council of Hong Kong SAR. C.Y.N. and C.T.C. are supported by AoE/P-02/12 from the Research Grants Council of Hong Kong SAR. M.N. and A.W.R. are supported by the National Science Foundation (grant no. DMR-1454836).
Author information
Authors and Affiliations
Contributions
L.T. and M.W. fabricated the devices and conducted the measurements. C.Y.N., M.N., A.W.R. and C.T.C. performed the theoretical calculations. H.B.C. conceived and supervised the experiment. All authors discussed the results and contributed to the writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 667 kb)
Rights and permissions
About this article
Cite this article
Tang, L., Wang, M., Ng, C. et al. Measurement of non-monotonic Casimir forces between silicon nanostructures. Nature Photon 11, 97–101 (2017). https://doi.org/10.1038/nphoton.2016.254
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2016.254
This article is cited by
-
Isotope effect on the Casimir force
Science China Physics, Mechanics & Astronomy (2023)
-
Observation and control of Casimir effects in a sphere-plate-sphere system
Nature Communications (2022)
-
Non-reciprocal energy transfer through the Casimir effect
Nature Nanotechnology (2022)
-
A naïve HMO study of the casimir effect
Journal of Mathematical Chemistry (2022)
-
A novel approach to construct self-assembled 3D MEMS arrays
Microsystem Technologies (2022)