Abstract
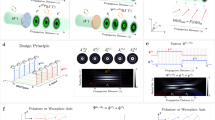
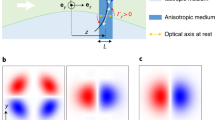
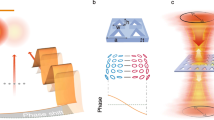
All known methods for transverse confinement and guidance of light rely on modification of the refractive index, that is, on the scalar properties of electromagnetic radiation1,2,3,4,5,6,7,8,9,10,11. Here, we disclose the concept of a dielectric waveguide that exploits vectorial spin–orbit interactions of light and the resulting geometric phases12,13,14,15,16,17. The approach relies on the use of anisotropic media with an optic axis that lies orthogonal to the propagation direction but is spatially modulated, so that the refractive index remains constant everywhere. A spin-controlled cumulative phase distortion is imposed on the beam, balancing diffraction for a specific polarization. As well as theoretical analysis, we present an experimental demonstration of the guidance using a series of discrete geometric-phase lenses made from liquid crystal. Our findings show that geometric phases may determine the optical guiding behaviour well beyond a Rayleigh length, paving the way to a new class of photonic devices. The concept is applicable to the whole electromagnetic spectrum.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Snyder, A. W. & Love, J. D. Optical Waveguide Theory (Chapman & Hall, 1983).
Yeh, P. & Yariv, A. Bragg reflection waveguides. Opt. Commun. 19, 427–430 (1976).
Joannopoulos, J. D., Villeneuve, P. R. & Fan, S. H. Photonic crystals: putting a new twist on light. Nature 386, 143–149 (1997).
Knight, J. C. Photonic crystal fibres. Nature 424, 847–851 (2003).
Russell, P. Photonic crystal fibers. Science 299, 358–362 (2003).
Almeida, V. R., Xu, Q., Barrios, C. A. & Lipson, M. Guiding and confining light in void nanostructure. Opt. Lett. 29, 1209–1211 (2004).
Weeber, J. C., Lacroute, Y. & Dereux, A. Optical near-field distributions of surface plasmon waveguide modes. Phys. Rev. B 68, 115401 (2003).
Yariv, A., Xu, Y., Lee, R. K. & Scherer, A. Coupled-resonator optical waveguide: a proposal and analysis. Opt. Lett. 24, 711–713 (1999).
Lin, Q. & Fan, S. Light guiding by effective gauge field for photons. Phys. Rev. X 4, 031031 (2014).
Cohen, O., Freedman, B., Fleischer, J. W., Segev, M. & Christodoulides, D. N. Grating-mediated waveguiding. Phys. Rev. Lett. 93, 103902 (2004).
Alberucci, A., Marrucci, L. & Assanto, G. Light confinement via periodic modulation of the refractive index. New J. Phys. 15, 083013 (2013).
Bliokh, K. Y., Rodriguez-Fortuno, F. J., Nori, F. & Zayats, A. V. Spin–orbit interactions of light. Nature Photon. 9, 796–808 (2015).
Cardano, F. & Marrucci, L. Spin–orbit photonics. Nature Photon. 9, 776–778 (2015).
Chiao, R. Y. & Wu, Y. S. Manifestations of Berry's topological phase for the photon. Phys. Rev. Lett. 57, 933 (1986).
Haldane, F. D. M. Path dependence of the geometric rotation of polarization in optical fibers. Opt. Lett. 11, 730–732 (1986).
Berry, M. V. The adiabatic phase and Pancharatnam's phase for polarized light. J. Mod. Opt. 34, 1401–1407 (1987).
Bhandari, R. Polarization of light and topological phases. Phys. Rep. 281, 1–64 (1997).
Peccianti, M., Conti, C., Assanto, G., De Luca, A. & Umeton, C. Routing of anisotropic spatial solitons and modulational instability in liquid crystals. Nature 432, 733–737 (2004).
Bomzon, Z., Kleiner, V. & Hasman, E. Pancharatnam–Berry phase in space-variant polarization-state manipulations with subwavelength gratings. Opt. Lett. 26, 1424–1426 (2001).
Marrucci, L., Manzo, C. & Paparo, D. Pancharatnam–Berry phase optical elements for wavefront shaping in the visible domain: switchable helical modes generation. Appl. Phys. Lett. 88, 221102 (2006).
Slussarenko, S. et al. Tunable liquid crystal q-plates with arbitrary topological charge. Opt. Express 19, 4085–4090 (2011).
Yu, N. & Capasso, F. Flat optics with designer metasurfaces. Nature Mater. 13, 139–150 (2014).
Lin, D., Fan, P., Hasman, E. & Brongersma, M. L. Dielectric gradient metasurface optical elements. Science 345, 298–302 (2014).
Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. A 44, 247–262 (1956).
Liberman, V. S. & Zel'dovich, B. Y. Spin–orbit interaction of a photon in an inhomogeneous medium. Phys. Rev. A 46, 5199–5207 (1992).
Bliokh, K. Y. & Bliokh, Y. P. Modified geometrical optics of a smoothly inhomogeneous isotropic medium: the anisotropy, Berry phase, and the optical Magnus effect. Phys. Rev. E 70, 026605 (2004).
Lin, C., Cohen, L. G. & Kogelnik, H. Optical-pulse equalization of low-dispersion transmission in single-mode fibers in the 1.3–1.7-μm spectral region. Opt. Lett. 5, 476–478 (1980).
Armstrong, J. A., Bloembergen, N., Ducuing, J. & Pershan, P. S. Interactions between light waves in a nonlinear dielectric. Phys. Rev. 127, 1918–1939 (1962).
Hasman, E., Kleiner, V., Biener, G. & Niv, A. Polarization dependent focusing lens by use of quantized Pancharatnam–Berry phase diffractive optics. Appl. Phys. Lett. 82, 328–330 (2003).
Roux, F. S. Geometric phase lens. J. Opt. Soc. Am. A 23, 476–482 (2006).
Berry, M. Pancharatnam, virtuoso of the Poincaré sphere: an appreciation. Curr. Sci. 67, 220–223 (1994).
Oskooi, A. F. et al. MEEP: a flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 181, 687–702 (2010).
Marrucci, L., Manzo, C. & Paparo, D. Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media. Phys. Rev. Lett. 96, 163905 (2006).
Nersisyan, S., Tabiryan, N., Steeves, D. M. & Kimball, B. R. Fabrication of liquid crystal polymer axial waveplates for UV-IR wavelengths. Opt. Express 17, 11926–11934 (2009).
Alexeyev, C. N. Circular array of anisotropic fibers: a discrete analog of a q plate. Phys. Rev. A 86, 063830 (2012).
Chigrinov, V. G., Kozenkov, V. M. & Kwok, H. S. Photoalignment of Liquid Crystalline Materials: Physics and Applications (Wiley, 2008).
Piccirillo, B., D'Ambrosio, V., Slussarenko, S., Marrucci, L. & Santamato, E. Photon spin-to-orbital angular momentum conversion via an electrically tunable q-plate. Appl. Phys. Lett. 97, 241104 (2010).
Sun, H. Thin lens equation for a real laser beam with weak lens aperture truncation. Opt. Eng. 37, 2906–2913 (1998).
Acknowledgements
The work in Naples was supported by the 7th Framework Programme of the European Commission, within the Future Emerging Technologies programme, under grant no. 255914 (PHORBITECH), and by the European Research Council (ERC), under grant no. 694683 (PHOSPhOR). A.A. and G.A. thank the Academy of Finland for financial support through FiDiPro grant no. 282858. C.P.J. gratefully acknowledges Fundação para a Ciência e a Tecnologia, POPH-QREN and FSE (FCT, Portugal) for fellowship no. SFRH/BPD/77524/2011.
Author information
Authors and Affiliations
Contributions
This work was jointly conceived by A.A., C.P.J., G.A. and L.M. S.S. designed and carried out the experiment, with the help and supervision of B.P., E.S. and L.M. A.A. and C.P.J. developed the theory and performed the numerical simulations, with the help and supervision of L.M. and G.A. All authors discussed the results and contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1153 kb)
Rights and permissions
About this article
Cite this article
Slussarenko, S., Alberucci, A., Jisha, C. et al. Guiding light via geometric phases. Nature Photon 10, 571–575 (2016). https://doi.org/10.1038/nphoton.2016.138
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2016.138
This article is cited by
-
Experimental observation of Berry phases in optical Möbius-strip microcavities
Nature Photonics (2023)
-
The geometric phase in nonlinear frequency conversion
Frontiers of Physics (2022)
-
Polarisation optics for biomedical and clinical applications: a review
Light: Science & Applications (2021)
-
Structured light
Nature Photonics (2021)
-
Light guiding by artificial gauge fields
Nature Photonics (2019)