Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Hanbury Brown and Twiss measurements in curved space

Nature Photonics volume 10, pages 106–110 (2016)Cite this article

Subjects

Abstract

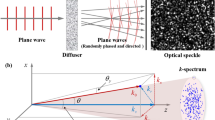
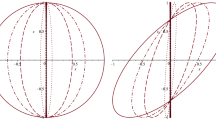
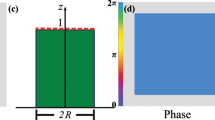
When Hanbury Brown and Twiss (HBT) proposed their technique of intensity correlation measurements1,2,3 to examine the angular size of stars in the visible range, they challenged the common conception of quantum mechanics and kicked off a discussion that led to the establishment of quantum optics4,5,6. In this Letter we revisit this fundamental technique and study its implications in the presence of space curvature. To this end we theoretically and experimentally investigate the evolution of speckle patterns propagating along two-dimensional surfaces of constant positive and negative Gaussian curvature, defying the notion that light always gains spatial coherence during free-space propagation. We also discuss the measurability of the traversed space's curvature utilizing HBT from an inhabitant's point of view. Through their symmetry, surfaces with constant Gaussian curvature act as analogue models for universes possessing non-vanishing cosmological constants.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Collection of surfaces with constant Gaussian curvature K.
Figure 2: Experimental set-up.
Figure 3: Experimental measurements of the second-order DOC function.
Figure 4: Simulations of speckle evolution on curved surfaces.

References

  1. Hanbury Brown, R. & Twiss, R. Q. Correlation between photons in two coherent beams of light. Nature 177, 27–29 (1956).

    Article  ADS  Google Scholar 

  2. Hanbury Brown, R. & Twiss, R. Q. A test of a new type of interstellar interferometer on Sirius. Nature 178, 1046–1048 (1956).

    Article  ADS  Google Scholar 

  3. Hanbury Brown, R., Davis, J. & Allen, L. R. The angular diameters of 32 stars. Mon. Not. R. Astron. Soc. 167, 121–136 (1974).

    Article  ADS  Google Scholar 

  4. Purcell, E. M. The question of correlation between photons in coherent light rays. Nature 178, 1449–1450 (1956).

    Article  ADS  Google Scholar 

  5. Glauber, R. J. Photon correlations. Phys. Rev. Lett. 10, 84–86 (1963).

    Article  ADS  MathSciNet  Google Scholar 

  6. Glauber, R. J. Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766–2788 (1963).

    Article  ADS  MathSciNet  Google Scholar 

  7. Foellmi, C. Intensity interferometry and the second-order correlation function g(2) in astrophysics. Astron. Astrophys. 507, 1719–1727 (2009).

    Article  ADS  Google Scholar 

  8. Malvimat, V., Wucknitz, O. & Saha, P. Intensity interferometry with more than two detectors? Mon. Not. R. Astron. Soc 437, 798–803 (2014).

    Article  ADS  Google Scholar 

  9. Altman, E., Demler, E. & Lukin, M. D. Probing many-body states of ultracold atoms via noise correlations. Phys. Rev. A 70, 013603 (2004).

    Article  ADS  Google Scholar 

  10. Schellekens, M. et al. Hanbury Brown Twiss effect for ultracold quantum gases. Science 310, 648–651 (2005).

    Article  ADS  Google Scholar 

  11. Fölling, S. et al. Spatial quantum noise interferometry in expanding ultracold atom clouds. Nature 434, 481–484 (2005).

    Article  ADS  Google Scholar 

  12. Perrin, A. et al. Hanbury Brown and Twiss correlations across the Bose-Einstein condensation threshold. Nature Phys. 8, 195–198 (2012).

    Article  ADS  Google Scholar 

  13. Boal, D. H., Gelbke, C.-K. & Jennings, B. K. Intensity interferometry in subatomic physics. Rev. Mod. Phys. 62, 553–602 (1990).

    Article  ADS  Google Scholar 

  14. Adams, J. et al. Azimuthally sensitive Hanbury Brown-Twiss interferometry in Au+Au collisions at . Phys. Rev. Lett. 93, 012301 (2004).

    Article  ADS  Google Scholar 

  15. Müller, B., Schukraft, J. & Wyslouch, B. First results from Pb+Pb collisions at the LHC. Annu. Rev. Nucl. Part. Sci. 62, 361–386 (2012).

    Article  ADS  Google Scholar 

  16. Bromberg, Y., Lahini, Y., Small, E. & Silberberg, Y. Hanbury Brown and Twiss interferometry with interacting photons. Nature Photon. 4, 721–726 (2010).

    Article  ADS  Google Scholar 

  17. Batz, S. & Peschel, U. Linear and nonlinear optics in curved space. Phys. Rev. A 78, 043821 (2008).

    Article  ADS  Google Scholar 

  18. Schultheiss, V. H. et al. Optics in curved space. Phys. Rev. Lett. 105, 143901 (2010).

    Article  ADS  Google Scholar 

  19. Genov, D. A., Zhang, S. & Zhang, X. Mimicking celestial mechanics in metamaterials. Nature Phys. 5, 687–692 (2009).

    Article  ADS  Google Scholar 

  20. Danner, A. J., Tyc, T. & Leonhardt, U. Controlling birefringence in dielectrics. Nature Photon. 5, 357–359 (2011).

    Article  ADS  Google Scholar 

  21. Sheng, C., Liu, H., Wang, Y., Zhu, S. N. & Genov, D. A. Trapping light by mimicking gravitational lensing. Nature Photon. 7, 902–906 (2013).

    Article  ADS  Google Scholar 

  22. Xu, L. & Chen, H. Conformal transformation optics. Nature Photon. 9, 15–23 (2015).

    Article  ADS  Google Scholar 

  23. Saleh, B. E. A. & Teich, M. C. Fundamentals of Photonics (Wiley, 1991).

    Book  Google Scholar 

  24. Foley, J. T. & Zubairy, M. S. The directionality of Gaussian Schell-model beams. Opt. Commun. 26, 297–300 (1978).

    Article  ADS  Google Scholar 

  25. Friberg, A. T. & Sudol, R. J. Propagation parameters of Gaussian Schell-model beams. Opt. Commun. 41, 383–387 (1982).

    Article  ADS  Google Scholar 

  26. Leonhardt, U. Perfect imaging without negative refraction. New J. Phys. 11, 093040 (2009).

    Article  ADS  Google Scholar 

  27. Goodman, J. W. Statistical Optics (Wiley, 2000).

    Google Scholar 

  28. Lo, K. Y. Mega-masers and galaxies. Annu. Rev. Astron. Astrophys. 43, 625–676 (2005).

    Article  ADS  Google Scholar 

  29. Reed, I. S. On a moment theorem for complex Gaussian processes. IRE Trans. Inform. Theor. 8, 194–195 (1962).

    Article  MathSciNet  Google Scholar 

  30. Picinbono, B. & Boileau, E. Higher-order coherence functions of optical fields and phase fluctuations. J. Opt. Soc. Am. 58, 784–789 (1968).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors would like to express their gratitude to R. Keding and P. Schrehardt at the glass workshop of the Max Planck Institute for the Science of Light (Erlangen) for their expertise in glass working. We are also grateful to T. Pertsch and F. Eilenberger from the University of Jena for providing a phase modulator. We gratefully acknowledge financial support by Deutsche Forschungsgemeinschaft (DFG) in the frame work of project PE 523/10-1 and the Cluster of Excellence Engineering of Advanced Materials (EAM).

Author information

Authors and Affiliations

  1. Institute of Optics, Information and Photonics, Friedrich-Alexander University Erlangen-Nürnberg (FAU), Haberstr. 9a, Erlangen, 91058, Germany

    Vincent H. Schultheiss, Sascha Batz & Ulf Peschel

  2. Institute of Condensed Matter Theory and Solid State Optics, Friedrich-Schiller-University Jena, Max-Wien-Platz 1, Jena, 07743, Germany

    Ulf Peschel

Authors
  1. Vincent H. Schultheiss
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sascha Batz
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ulf Peschel
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

V.H.S. and S.B. derived the theory, V.H.S. and U.P. conceived and designed the experiments, V.H.S. performed the experiments and analysed the data, S.B. provided the MATLAB code for the simulations, V.H.S, S.B. and U.P. co-wrote the paper.

Corresponding author

Correspondence to Ulf Peschel.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 1195 kb)

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Schultheiss, V., Batz, S. & Peschel, U. Hanbury Brown and Twiss measurements in curved space. Nature Photon 10, 106–110 (2016). https://doi.org/10.1038/nphoton.2015.244

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphoton.2015.244

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing