Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Dynamic consequences of optical spin–orbit interaction

Nature Photonics volume 9, pages 809–812 (2015)Cite this article

Subjects

Abstract

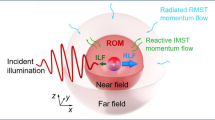
Field symmetries and conservation laws are closely associated through Noether's theorem. Light field inhomogeneities lead to changes in linear and angular momenta and, consequently, to radiation pressure1,2, spin or rotation of objects3,4. Here we discuss a new type of mechanical action originating in the exchange between spin and orbital angular momenta. We demonstrate theoretically and experimentally that, when mirror and central symmetries of scattering are broken, a force appears acting perpendicularly to the direction of propagation. This new force completes the set of non-conservative forces (radiation pressure and tractor beams) that can be generated with unstructured light beams.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Scattering of circularly polarized light off a spherical particle located at an interface between two dielectric media.
Figure 2: Lateral force on Mie-size particles.
Figure 3: Experimental data.

Similar content being viewed by others

References

  1. Lebedev, P. Untersuchungen über die druckkräfte des lichtes. Ann. Phys. (Leipz.) 6, 433–458 (1901).

    Article  ADS  Google Scholar 

  2. Nichols, E. F. & Hull, G. F. A preliminary communication on the pressure of heat and light radiation. Phys. Rev. 13, 307–320 (1901).

    ADS  Google Scholar 

  3. Beth, R. A. Mechanical detection and measurement of the angular momentum of light. Phys. Rev. 50, 115–125 (1936).

    Article  ADS  Google Scholar 

  4. Friese, M. E. J., Nieminen, T. A., Heckenberg, N. R. & Rubinsztein-Dunlop, H. Optical alignment and spinning of laser-trapped microscopic particles. Nature 394, 348–350 (1998).

    Article  ADS  Google Scholar 

  5. Liberman, V. S. & Zel'dovich, B. Y. Spin–orbit interaction of a photon in an inhomogeneous medium. Phys. Rev. A 46, 5199–5207 (1992).

    Article  ADS  Google Scholar 

  6. Onada, M., Murakami, S. & Nagaose, N. Hall effect of light. Phys. Rev. Lett. 93, 083901 (2004).

    Article  ADS  Google Scholar 

  7. Schwartz, C. & Dogariu, A. Conservation of angular momentum of light in single scattering. Opt. Express 14, 8425–8433 (2006).

    Article  ADS  Google Scholar 

  8. Haefner, D., Sukhov, S. & Dogariu, A. Spin Hall effect of light in spherical geometry. Phys. Rev. Lett. 102, 123903 (2009).

    Article  ADS  Google Scholar 

  9. Rodríguez-Fortuño, F. J. et al. Near-field interference for the unidirectional excitation of electromagnetic guided modes. Science 340, 328–330 (2013).

    Article  ADS  Google Scholar 

  10. Petersen, J., Volz, J. & Rauschenbeutel, A. Chiral nanophotonic waveguide interface based on spin–orbit interaction of light. Science 346, 67–71 (2014).

    Article  ADS  Google Scholar 

  11. Fedoseyev, V. G. Transverse forces related to the transverse shifts of reflected and transmitted light beams. J. Opt. 15, 014017 (2013).

    Article  ADS  Google Scholar 

  12. Haefner, D., Sukhov, S. & Dogariu, A. Conservative and nonconservative torques in optical binding. Phys. Rev. Lett. 103, 173602 (2009).

    Article  ADS  Google Scholar 

  13. Kajorndejnukul, V., Ding, W., Sukhov, S., Qiu, C. W. & Dogariu, A. Linear momentum increase and negative optical forces at dielectric interface. Nature Photon. 7, 787–790 (2013).

    Article  ADS  Google Scholar 

  14. Borghese, F., Denti, P. & Saija, R. Scattering from Model Nonspherical Particles: Theory and Applications to Environmental Physics (Springer, 2007).

    MATH  Google Scholar 

  15. Chaumet, P. C. & Nieto-Vesperinas, M. Time-averaged total force on a dipolar sphere in an electromagnetic field. Opt. Lett. 25, 1065–1067 (2000).

    Article  ADS  Google Scholar 

  16. Novotny, L. & Hecht, B. Principles of Nano-Optics (Cambridge University Press, 2006).

    Book  Google Scholar 

  17. Wang, S. B. & Chan, C. T. Lateral optical force on chiral particles near a surface. Nature Commun. 5, 3307 (2014).

    Article  ADS  Google Scholar 

  18. Bekshaev, A. Y., Angelsky, O. V., Hanson, S. G. & Zenkova, C. Y. Scattering of inhomogeneous circularly polarized optical field and mechanical manifestation of the internal energy flows. Phys. Rev. A 86, 023847 (2012).

    Article  ADS  Google Scholar 

  19. Salandrino, A., Fardad, S. & Christodoulides, D. N. Generalized Mie theory of optical forces. J. Opt. Soc. Am. B 29, 855–866 (2012).

    Article  ADS  Google Scholar 

  20. Bekshaev, A. Y., Bliokh, K. Y. & Nori, F. Transverse spin and momentum in two-wave interference. Phys. Rev. X 5, 011039 (2015).

    Google Scholar 

  21. Sukhov, S., Kajorndejnukul, V., Broky, J. & Dogariu, A. Forces in Aharonov–Bohm optical setting. Optica 1, 383–387 (2014).

    Article  ADS  Google Scholar 

  22. Omenyi, S. N., Neumann, A. W. & van Oss, C. J. Attraction and repulsion of solid particles by solidification fronts I. Thermodynamic effects. J. Appl. Phys. 52, 789–795 (1981).

    Article  ADS  Google Scholar 

  23. Wunenburger, R. et al. Fluid flows driven by light scattering. J. Fluid Mech. 666, 273–307 (2011).

    Article  ADS  Google Scholar 

  24. Kajorndejnukul, V., Sukhov, S. & Dogariu, A. Controlled transport through optical advection. Sci. Rep. 5, 14861 (2015).

    Article  ADS  Google Scholar 

  25. Rotne, J. & Prager, S. Variational treatment of hydrodynamic interaction in polymers. J. Chem. Phys. 50, 4831–4837 (1969).

    Article  ADS  Google Scholar 

  26. Ladavac, K. & Grier, D. G. Colloidal hydrodynamic coupling in concentric optical vortices. Europhys. Lett. 70, 548–554 (2005).

    Article  ADS  Google Scholar 

  27. Happel, J. & Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media (Martinus Nijhoff, 1983).

    MATH  Google Scholar 

  28. Danov, K., Aust, R., Durst, F. & Lange, U. Influence of the surface viscosity on the hydrodynamic resistance and surface diffusivity of a large brownian particle. J. Colloid Interface Sci. 175, 36–45 (1995).

    Article  ADS  Google Scholar 

  29. Pilat, D. W. et al. Dynamic measurement of the force required to move a liquid drop on a solid surface. Langmuir 28, 16812−16820 (2012).

    Article  Google Scholar 

  30. Gao, Y. & Kilfoil, M. L. Accurate detection and complete tracking of large populations of features in three dimensions. Opt. Express 17, 4685–4704 (2009).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was partially supported by NSF grant no. 1159530.

Author information

Authors and Affiliations

  1. CREOL, The College of Optics and Photonics, University of Central Florida, 4000 Central Florida Boulevard, Orlando, 32816, Florida, USA

    Sergey Sukhov, Veerachart Kajorndejnukul, Roxana Rezvani Naraghi & Aristide Dogariu

  2. Department of Physics, University of Central Florida, 4000 Central Florida Boulevard, Orlando, 32816, Florida, USA

    Roxana Rezvani Naraghi

Authors
  1. Sergey Sukhov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Veerachart Kajorndejnukul
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Roxana Rezvani Naraghi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Aristide Dogariu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S.S. and A.D. conceived the idea and designed the experiments. S.S. performed theoretical analysis. V.K. and R.R.N. performed the experiments. S.S. and V.K. contributed materials/analysis tools. S.S., V.K., R.R.N. and A.D. analysed the data. S.S. and A.D. wrote the paper.

Corresponding author

Correspondence to Aristide Dogariu.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 684 kb)

Supplementary information

Supplementary movie 1 (AVI 26168 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sukhov, S., Kajorndejnukul, V., Naraghi, R. et al. Dynamic consequences of optical spin–orbit interaction. Nature Photon 9, 809–812 (2015). https://doi.org/10.1038/nphoton.2015.200

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphoton.2015.200

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing