Abstract
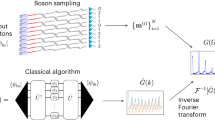
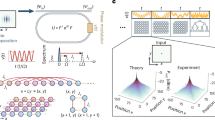
Controllable quantum devices open novel directions to both quantum computation and quantum simulation. Recently, a problem known as boson sampling has been shown to provide a pathway for solving a computationally intractable problem without the need for a full quantum computer, instead using a linear optics quantum set-up. In this work, we propose a modification of boson sampling for the purpose of quantum simulation. In particular, we show that, by means of squeezed states of light coupled to a boson sampling optical network, one can generate molecular vibronic spectra, a problem for which no efficient classical algorithm is currently known. We provide a general framework for carrying out these simulations via unitary quantum optical transformations and supply specific molecular examples for future experimental realization.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Deutsch, D. & Jozsa, R. Rapid solution of problems by quantum computation. Proc. R. Soc. Lond. A 439, 553–558 (1992).
Grover, L. K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79, 325–328 (1997).
Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41, 303–332 (1999).
Georgescu, I. M., Ashhab, S. & Nori, F. Quantum simulation. Rev. Mod. Phys. 86, 153–185 (2014).
Aspuru-Guzik, A. & Walther, P. Photonic quantum simulators. Nature Phys. 8, 285–291 (2012).
Bloch, I., Dalibard, J. & Nascimbène, S. Quantum simulations with ultracold quantum gases. Nature Phys. 8, 267–276 (2012).
Blatt, R. & Roos, C. F. Quantum simulations with trapped ions. Nature Phys. 8, 277–284 (2012).
Lloyd, S. Universal quantum simulators. Science 273, 1073–1077 (1996).
Aspuru-Guzik, A., Dutoi, A. D., Love, P. J. & Head-Gordon, M. Simulated quantum computation of molecular energies. Science 309, 1704–1707 (2005).
Kassal, I., Whitfield, J. D., Perdomo-Ortiz, A., Yung, M.-H. & Aspuru-Guzik, A. Simulating chemistry using quantum computers. Ann. Rev. Phys. Chem. 62, 185–207 (2011).
Babbush, R., McClean, J., Wecker, D., Aspuru-Guzik, A. & Wiebe, N. Chemical basis of Trotter–Suzuki errors in quantum chemistry simulation. Phys. Rev. A 91, 022311 (2015).
Aaronson, S. & Arkhipov, A. in Proceedings of the 43rd Annual ACM Symposium on Theory of Computing (eds Fortnow, L. & Vadhan, S.) 333–342 (ACM, 2011).
Spring, J. B. et al. Boson sampling on a photonic chip. Science 339, 798–801 (2013).
Broome, M. A. et al. Photonic boson sampling in a tunable circuit. Science 339, 794–798 (2013).
Crespi, A. et al. Integrated multimode interferometers with arbitrary designs for photonic boson sampling. Nature Photon. 7, 545–549 (2013).
Tillmann, M. et al. Experimental boson sampling. Nature Photon. 7, 540–544 (2013).
Shchesnovich, V. S. Conditions for an experimental boson-sampling computer to disprove the extended Church–Turing thesis. Preprint at http://arxiv.org/abs/1403.4459v6 (2014).
Rohde, P. P., Motes, K. R., Knott, P. A. & Munro, W. J. Will boson-sampling ever disprove the extended Church–Turing thesis? Preprint at http://arxiv.org/abs/1401.2199v2 (2014).
Sharp, T. E. & Rosenstock, H. M. Franck–Condon factors for polyatomic molecules. J. Chem. Phys. 41, 3453–3463 (1964).
Doktorov, E. V., Malkin, I. A. & Man'ko, V. I. Dynamical symmetry of vibronic transitions in polyatomic molecules and the Franck–Condon principle. J. Mol. Spectrosc. 64, 302–326 (1977).
Malmqvist, P.-Å. & Forsberg, N. Franck–Condon factors for multidimensional harmonic oscillators. Chem. Phys. 228, 227–240 (1998).
Ruhoff, P. T. & Ratner, M. A. Algorithm for computing Franck–Condon overlap integrals. Int. J. Quantum Chem. 77, 383–392 (2000).
Jankowiak, H.-C., Stuber, J. L. & Berger, R. Vibronic transitions in large molecular systems: rigorous prescreening conditions for Franck–Condon factors. J. Chem. Phys. 127, 234101 (2007).
Santoro, F., Lami, A., Improta, R. & Barone, V. Effective method to compute vibrationally resolved optical spectra of large molecules at finite temperature in the gas phase and in solution. J. Chem. Phys. 126, 184102 (2007).
Hachmann, J. et al. The Harvard Clean Energy Project: large-scale computational screening and design of organic photovoltaics on the world community grid. J. Phys. Chem. Lett. 2, 2241–2251 (2011).
Gross, M. et al. Improving the performance of doped π-conjugated polymers for use in organic light-emitting diodes. Nature 405, 661–665 (2000).
Dierksen, M. & Grimme, S. The vibronic structure of electronic absorption spectra of large molecules: a time-dependent density functional study on the influence of ‘exact’ Hartree–Fock exchange. J. Phys. Chem. A 108, 10225–10237 (2004).
Hayes, D., Wen, J., Panitchayangkoon, G., Blankenship, R. E. & Engel, G. S. Robustness of electronic coherence in the Fenna–Matthews–Olson complex to vibronic and structural modifications. Faraday Discuss. 150, 459–469 (2011).
Choi, K.-W., Lee, J.-H. & Kim, S. K. Ionization spectroscopy of DNA base: vacuum-ultraviolet mass-analyzed threshold ionization spectroscopy of jet-cooled thymine. J. Am. Chem. Soc. 127, 15674–15675 (2005).
Duschinsky, F. The importance of the electron spectrum in multiatomic molecules. Concerning the Franck–Condon principle. Acta Physicochim. URSS 7, 551–566 (1937).
Ma, X. & Phodes, W. Multimode squeeze operators and squeezed states. Phys. Rev. A 41, 4625–4631 (1990).
Scheel, S. Permanents in linear optical networks. Preprint at http://arxiv.org/abs/quant-ph/0406127 (2004).
Huh, J. Unified Description of Vibronic Transitions with Coherent States. PhD thesis, Goethe Univ. Frankfurt (2011).
Lund, A. P. et al. Boson sampling from a Gaussian state. Phys. Rev. Lett. 113, 100502 (2014).
Santoro, F., Lami, A., Improta, R., Bloino, J. & Barone, V. Effective method for the computation of optical spectra of large molecules at finite temperature including the Duschinsky and Herzberg–Teller effect: the Q x band of porphyrin as a case study. J. Chem. Phys. 128, 224311 (2008).
Rahimi-Keshari, S., Lund, A. P. & Ralph, T. C. What can quantum optics say about complexity theory? Preprint at http://arxiv.org/abs/1408.3712v1 (2014).
Olson, J. P., Seshadreesan, K. P., Motes, K. R., Rohde, P. P. & Dowling, J. P. Sampling arbitrary photon-added or photon-subtracted squeezed states is in the same complexity class as boson sampling. Phys. Rev. A 91, 022317 (2015).
Berger, R. & Klessinger, M. Algorithms for exact counting of energy levels of spectroscopic transitions at different temperatures. J. Comput. Chem. 18, 1312–1319 (1997).
Berger, R., Fischer, C. & Klessinger, M. Calculation of the vibronic fine structure in electronic spectra at higher temperatures. 1. Benzene and pyrazine. J. Phys. Chem. 102, 7157–7176 (1998).
Leach, S. et al. He I photoelectron spectroscopy of four isotopologues of formic acid: HCOOH, HCOOD, DCOOH and DCOOD. Chem. Phys. 286, 15–43 (2003).
Carolan, J. et al. On the experimental verification of quantum complexity in linear optics. Nature Photon. 8, 621–626 (2014).
Josse, V., Sabuncu, M., Cerf, N., Leuchs, G. & Andersen, U. Universal optical amplification without nonlinearity. Phys. Rev. Lett. 96, 163602 (2006).
Yoshikawa, J.-I. et al. Demonstration of deterministic and high fidelity squeezing of quantum information. Phys. Rev. A 76, 060301(R) (2007).
Miwa, Y. et al. Exploring a new regime for processing optical qubits: squeezing and unsqueezing single photons. Phys. Rev. Lett. 113, 013601 (2014).
Jerrum, M., Sinclair, A. & Vigoda, E. A polynomial-time approximation algorithm for the permanent of a matrix with nonnegative entries. J. ACM 51, 671–697 (2004).
Huh, J., Neff, M., Rauhut, G. & Berger, R. Franck–Condon profiles in photodetachment–photoelectron spectra of HS2− and DS2− based on vibrational configuration interaction wavefunctions. Mol. Phys. 108, 409–423 (2010).
Huh, J. & Berger, R. Application of time-independent cumulant expansion to calculation of Franck–Condon profiles for large molecular systems. Faraday Discuss. 150, 363–373 (2011).
Huh, J. & Berger, R. Coherent state-based generating function approach for Franck–Condon transitions and beyond. J. Phys. Conf. Ser. 380, 012019 (2012).
Kan, R. From moments of sum to moments of product. J. Multivariate Anal. 99, 542–554 (2008).
Acknowledgements
We thank R. Berger for permission to use the vibronic structure program hotFCHT for our research. J.H. and A.A.-G. acknowledge a Defense Threat Reduction Agency grant HDTRA1-10-1-0046 and the Air Force Office of Scientific Research grant FA9550-12-1-0046. J.R.M. is supported by the Department of Energy Computational Science Graduate Fellowship under grant number DE-FG02-97ER25308. G.G.G. and A.A.-G. acknowledge support from Natural Sciences Foundation (NSF) Grant No. CHE-1152291. B.P. and A.A.-G. acknowledge support from the Science and Technology Center for Integrated Quantum Materials, NSF Grant No. DMR-1231319. Furthermore, A.A.-G. is grateful for support from the Defense Advanced Research Projects Agency grant N66001-10-1-4063, and the Corning Foundation for their generous support.
Author information
Authors and Affiliations
Contributions
J.H., G.G.G. and A.A.-G. conceived and designed the experiments. J.H. and G.G.G. performed the simulations. J.H., G.G.G., B.P. and J.R.M. contributed materials and/or analysis tools. J.H., G.G.G., B.P., J.R.M. and A.A.-G. worked on the theory, analysed the data and wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 331 kb)
Rights and permissions
About this article
Cite this article
Huh, J., Guerreschi, G., Peropadre, B. et al. Boson sampling for molecular vibronic spectra. Nature Photon 9, 615–620 (2015). https://doi.org/10.1038/nphoton.2015.153
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2015.153
This article is cited by
-
Quantum-inspired classical algorithms for molecular vibronic spectra
Nature Physics (2024)
-
Engineering multimode interactions in circuit quantum acoustodynamics
Nature Physics (2024)
-
Efficiently simulating the work distribution of multiple identical bosons with boson sampling
Frontiers of Physics (2024)
-
Programmability empowering quantum boson sampling
Nature Computational Science (2023)
-
Non-linear Boson Sampling
npj Quantum Information (2023)