Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Network of time-multiplexed optical parametric oscillators as a coherent Ising machine

Nature Photonics volume 8, pages 937–942 (2014)Cite this article

Subjects

Abstract

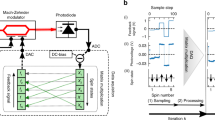
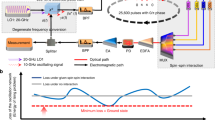
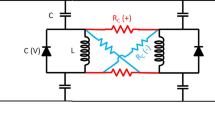
Finding the ground states of the Ising Hamiltonian1 maps to various combinatorial optimization problems in biology, medicine, wireless communications, artificial intelligence and social network. So far, no efficient classical and quantum algorithm is known for these problems and intensive research is focused on creating physical systems—Ising machines—capable of finding the absolute or approximate ground states of the Ising Hamiltonian2,3,4,5,6. Here, we report an Ising machine using a network of degenerate optical parametric oscillators (OPOs). Spins are represented with above-threshold binary phases of the OPOs and the Ising couplings are realized by mutual injections7. The network is implemented in a single OPO ring cavity with multiple trains of femtosecond pulses and configurable mutual couplings, and operates at room temperature. We programmed a small non-deterministic polynomial time-hard problem on a 4-OPO Ising machine and in 1,000 runs no computational error was detected.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Principle of operation of OPO Ising machine.
Figure 2: Experimental set-up.
Figure 3: Slow detector results.
Figure 4: Fast detector results.

Similar content being viewed by others

References

  1. Barahona, F. On the computational complexity of Ising spin glass models. J. Phys. A 15, 3241 (1982).

    Article  ADS  MathSciNet  Google Scholar 

  2. Kirkpatrick, S., Gelatt, D. Jr & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671–680 (1983).

    Article  ADS  MathSciNet  Google Scholar 

  3. Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse Ising model. Phys. Rev. E 58, 5355 (1998).

    Article  ADS  Google Scholar 

  4. Santoro, G. E., Martoak, R., Tosatti, E. & Car, R. Theory of quantum annealing of an Ising spin glass. Science 295, 2427–2430 (2002).

    Article  ADS  Google Scholar 

  5. Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472–475 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  6. Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011).

    Article  ADS  Google Scholar 

  7. Wang, Z., Marandi, A., Wen, K., Byer, R. L. & Yamamoto, Y. Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. A 88, 063853 (2013).

    Article  ADS  Google Scholar 

  8. Kitchen, D. B., Decornez, H., Furr, J. R. & Bajorath, J. Docking and scoring in virtual screening for drug discovery: methods and applications. Nature Rev. Drug Discov. 3, 935–949 (2004).

    Article  Google Scholar 

  9. Witten, I. H., Frank, E. & Hall, M. A. Data Mining: Practical Machine Learning Tools and Techniques (Morgan Kaufmann, 2005).

    MATH  Google Scholar 

  10. Papadimitriou, C. H. & Steiglitz, K. Combinatorial Optimization: Algorithms and Complexity (Courier Dover, 1998).

    MATH  Google Scholar 

  11. Hochbaum, D. S. Approximation Algorithms for NP-hard Problems (PWS, 1996).

    MATH  Google Scholar 

  12. Goemans, M. X. & Williams, D. P. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming. J. ACM 42, 1115–1145 (1995).

    Article  MathSciNet  Google Scholar 

  13. Adleman, L. M. Molecular computation of solutions to combinatorial problems. Science 266, 1021–1023 (1994).

    Article  ADS  Google Scholar 

  14. Wu, K., de Abajo, J. G., Soci, C., Shum, P. P. & Zheludev, N. I. An optical fiber network oracle for NP-complete problems. Light 3, e147 (2014).

    Article  Google Scholar 

  15. Dickson, N. G. et al. Thermally assisted quantum annealing of a 16-qubit problem. Nature Commun. 4, 1903 (2013).

    Article  ADS  MathSciNet  Google Scholar 

  16. Ronnow, T. F. et al. Defining and detecting quantum speedup. Science 345, 420–424 (2014).

    Article  ADS  Google Scholar 

  17. Marandi, A., Leindecker, N. C., Pervak, V. Byer, R. L. & Vodopyanov, K. L. Coherence properties of a broadband femtosecond mid-IR optical parametric oscillator operating at degeneracy. Opt. Express 20, 7255–7262 (2012).

    Article  ADS  Google Scholar 

  18. Roslund, J., De Araujo, R. M., Jiang, S., Fabre, C. & Treps, N. Wavelength-multiplexed quantum networks with ultrafast frequency combs. Nature Photon. 8, 109–113 (2014).

    Article  ADS  Google Scholar 

  19. Marandi, A., Leindecker, N. C., Vodopyanov, K. L. & Byer R. L. All-optical quantum random bit generation from intrinsically binary phase of parametric oscillators. Opt. Express 20, 19322–19330 (2012).

    Article  ADS  Google Scholar 

  20. Binder, K. & Young, A. P. Spin glasses: experimental facts, theoretical concepts, and open questions. Rev. Mod. Phys. 58, 801 (1986).

    Article  ADS  Google Scholar 

  21. Ising, E. Beitrag zur Theorie des Ferromagnetismus. Zeitschrift für Physik A, Hadrons and Nuclei 31, 253–258 (1925).

    Google Scholar 

  22. Kim, K. et al. Quantum simulation of frustrated Ising spins with trapped ions. Nature 465, 590–593 (2010).

    Article  ADS  Google Scholar 

  23. Simon, J. et al. Quantum simulation of antiferromagnetic spin chains in an optical lattice. Nature 472, 307–312 (2011).

    Article  ADS  Google Scholar 

  24. Utsunomiya, S., Takata, K. & Yamamoto, Y. Mapping of Ising models onto injection-locked laser systems. Opt. Express 19, 18091–18108 (2011).

    Article  ADS  Google Scholar 

  25. Nabors, C. D., Yang, S. T., Day, T. & Byer, R. L. Coherence properties of a doubly-resonant monolithic optical parametric oscillator. J. Opt. Soc. Am. B 7, 815–820 (1990).

    Article  ADS  Google Scholar 

  26. Wu, L., Kimble, H. J., Hall, J. L. & Wu, H. Generation of squeezed states by parametric down conversion. Phys. Rev. Lett. 57, 2520 (1986).

    Article  ADS  Google Scholar 

  27. Graham, R. in Coherence and Quantum Optics (eds Mandel, L. & Wolf, E.) 851–872 (Springer, 1973).

    Book  Google Scholar 

  28. Wolinsky, M. & Carmichael, H. J. Quantum noise in the parametric oscillator: from squeezed states to coherent-state superpositions. Phys. Rev. Lett. 60, 1836 (1988).

    Article  ADS  Google Scholar 

  29. Gottesman, D. The Heisenberg representation of quantum computers. Preprint at http://arxiv.org/abs/quant-ph/9807006 (1998).

  30. Galluccio, A., Loebl, M. & Vondrk, J. New algorithm for the Ising problem: partition function for finite lattice graphs. Phys. Rev. Lett. 84, 5924 (2000).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The authors thank S.E. Harris, H. Mabuchi, M. Armen, S. Utsunomiya, S. Tamate, K. Yan and Y. Haribara for discussions and K. Ingold, C.W. Rudy, C. Langrock and K. Urbanek for experimental support. The work is supported by the FIRST Quantum Information Processing project.

Author information

Authors and Affiliations

  1. E.L. Ginzton Laboratory, Stanford University, California, 94305, USA

    Alireza Marandi, Zhe Wang, Robert L. Byer & Yoshihisa Yamamoto

  2. National Institute of Informatics, Tokyo, 101-8403, Japan

    Alireza Marandi, Kenta Takata & Yoshihisa Yamamoto

  3. Department of Information and Communication Engineering, University of Tokyo, Tokyo, 113-8656, Japan

    Kenta Takata & Yoshihisa Yamamoto

Authors
  1. Alireza Marandi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhe Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kenta Takata
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Robert L. Byer
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yoshihisa Yamamoto
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.M. and Y.Y. conceived the idea and designed the experiment. A.M. and K.T. carried out the experiment. Z.W. performed the numerical simulations. Y.Y. and R.L.B. guided the work. A.M. wrote the manuscript, with input from all authors.

Corresponding author

Correspondence to Alireza Marandi.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 2667 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Marandi, A., Wang, Z., Takata, K. et al. Network of time-multiplexed optical parametric oscillators as a coherent Ising machine. Nature Photon 8, 937–942 (2014). https://doi.org/10.1038/nphoton.2014.249

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphoton.2014.249

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing