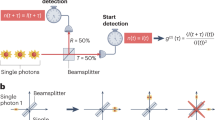
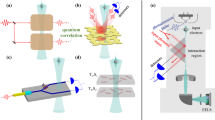
Abstract
The realization of strong interactions between individual photons is a long-standing goal of both fundamental and technological significance. Scientists have known for over half a century that light fields can interact inside nonlinear optical media, but the nonlinearity of conventional materials is negligible at the light powers associated with individual photons. Nevertheless, remarkable advances in quantum optics have recently culminated in the demonstration of several methods for generating optical nonlinearities at the level of individual photons. Systems exhibiting strong photon–photon interactions enable a number of unique applications, including quantum-by-quantum control of light fields, single-photon switches and transistors, all-optical deterministic quantum logic, and the realization of strongly correlated states of light and matter.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
References
Boyd, R. W. Nonlinear Optics (Academic, 2003).
Agrawal, G. Nonlinear Fiber Optics 5th edn (Academic, 2012).
Zipfel, W. R., Williams, R. M. & Webb, W. W. Nonlinear magic: Multiphoton microscopy in the biosciences. Nature Biotechnol. 21, 1369–1377 (2003).
Hell, S. W. Toward fluorescence nanoscopy. Nature Biotechnol. 21, 1347–1355 (2003).
Miller, D. A. B. Are optical transistors the logical next step? Nature Photon. 4, 3–5 (2010).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Muthukrishnan, A., Scully, M. O. & Zubairy, M. S. Quantum microscopy using photon correlations. J. Opt. B 6, S575 10.1088/1464-4266/6/6/017(2004).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nature Photon. 5, 222–229 (2011).
Franken, P. A. & Ward, J. F. Optical harmonics and nonlinear phenomena. Rev. Mod. Phys. 35, 23–39 (1963).
Byer, R. L. Quasi-phasematched nonlinear interactions and devices. J. Nonlinear Opt. Phys. Mater. 6, 549–592 (1997).
Milburn, G. J. Quantum optical Fredkin gate. Phys. Rev. Lett. 62, 2124–2127 (1989).
Imoto, N., Haus, H. A. & Yamamoto, Y. Quantum nondemolition measurement of the photon number via the optical Kerr effect. Phys. Rev. A 32, 2287–2292 (1985).
Harris, S. E., Field, J. E. & Imamoğlu, A. Nonlinear optical processes using electromagnetically induced transparency. Phys. Rev. Lett. 64, 1107–1110 (1990).
Turchette, Q. A., Hood, C. J., Lange, W., Mabuchi, H. & Kimble, H. J. Measurement of conditional phase shifts for quantum logic. Phys. Rev. Lett. 75, 4710–4713 (1995).
Haroche, S. & Raimond, J.-M. Exploring the Quantum: Atoms, Cavities, and Photons (Oxford Univ. Press, 2006).
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: An outlook. Science 339, 1169–1174 (2013).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Pan, J.-W. et al. Multiphoton entanglement and interferometry. Rev. Mod. Phys. 84, 777–838 (2012).
Schmidt, H. & Imamoğlu, A. Giant Kerr nonlinearities obtained by electromagnetically induced transparency. Opt. Lett. 21, 1936–1938 (1996).
Harris, S. E. & Hau, L. V. Nonlinear optics at low light levels. Phys. Rev. Lett. 82, 4611–4614 (1999).
Duan, L.-M. & Kimble, H. J. Scalable photonic quantum computation through cavity-assisted interactions. Phys. Rev. Lett. 92, 127902 (2004).
Gorshkov, A. V., Otterbach, J., Fleischhauer, M., Pohl, T. & Lukin, M. D. Photon–photon interactions via Rydberg blockade. Phys. Rev. Lett. 107, 133602 (2011).
Darquie, B. et al. Controlled single-photon emission from a single trapped two-level atom. Science 309, 454–456 (2005).
Tey, M. K. et al. Strong interaction between light and a single trapped atom without the need for a cavity. Nature Phys. 4, 924–927 (2008).
Hetet, G., Slodicka, L., Hennrich, M. & Blatt, R. Single atom as a mirror of an optical cavity. Phys. Rev. Lett. 107, 133002 (2011).
Wrigge, G., Gerhardt, I., Hwang, J., Zumofen, G. & Sandoghdar, V. Efficient coupling of photons to a single molecule and the observation of its resonance fluorescence. Nature Phys. 4, 60–66 (2008).
Birnbaum, K. M. et al. Photon blockade in an optical cavity with one trapped atom. Nature 436, 87–90 (2005).
Schuster, I. et al. Nonlinear spectroscopy of photons bound to one atom. Nature Phys. 4, 382–385 (2008).
Fushman, I. et al. Controlled phase shifts with a single quantum dot. Science 320, 769–772 (2008).
Dayan, B. et al. A photon turnstile dynamically regulated by one atom. Science 319, 1062–1065 (2008).
Volz, T. et al. Ultrafast all-optical switching by single photons. Nature Photon. 6, 605–609 (2012).
Tanji-Suzuki, H., Chen, W., Landig, R., Simon, J. & Vuletic, V. Vacuum-induced transparency. Science 333, 1266–1269 (2011).
Jaynes, E. & Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 51, 89–109 (1963).
Kubanek, A. et al. Two-photon gateway in one-atom cavity quantum electrodynamics. Phys. Rev. Lett. 101, 203602 (2008).
Koch, M. et al. Three-photon correlations in a strongly driven atom–cavity system. Phys. Rev. Lett. 107, 023601 (2011).
Michler, P. et al. A quantum dot single-photon turnstile device. Science 290, 2282–2285 (2000).
Pelton, M. et al. Efficient source of single photons: A single quantum dot in a micropost microcavity. Phys. Rev. Lett. 89, 233602 (2002).
Laucht, A. et al. Electrical control of spontaneous emission and strong coupling for a single quantum dot. New J. Phys. 11, 023034 (2009).
Faraon, A., Barclay, P. E., Santori, C., Fu, K.-M. C. & Beausoleil, R. G. Resonant enhancement of the zero-phonon emission from a colour centre in a diamond cavity. Nature Photon. 5, 301–305 (2011).
Hausmann, B. J. M. et al. Integrated diamond networks for quantum nanophotonics. Nano Lett. 12, 1578–1582 (2012).
Bajcsy, M. et al. Non-classical three-photon correlations with a quantum dot strongly coupled to a photonic-crystal nanocavity. Preprint at http://lanl.arXiv.org/abs/1307.3601v1 (2013).
Reinhard, A. et al. Strongly correlated photons on a chip. Nature Photon. 6, 93–96 (2012).
Witthaut, D., Lukin, M. D. & Sørensen, A. S. Photon sorters and QND detectors using single photon emitters. Europhys. Lett. 97, 50007 (2012).
Xu, S., Rephaeli, E. & Fan, S. Analytic properties of two-photon scattering matrix in integrated quantum systems determined by the cluster decomposition principle. Phys. Rev. Lett. 111, 223602 (2013).
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Fleischhauer, M., Imamoğlu, A. & Marangos, J. P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005).
Specht, H. P. et al. A single-atom quantum memory. Nature 473, 190–193 (2011).
Reiserer, A., Ritter, S. & Rempe, G. Nondestructive detection of an optical photon. Science 342, 1349–1351 (2013).
Tiecke, T. G. et al. Nanophotonic quantum phase switch with a single atom. Nature 508, 241–244 (2014).
Reiserer, A. et al. A quantum gate between a flying optical photon and a single trapped atom. Nature 508, 237–240 (2014).
Hammerer, K., Sørensen, A. S. & Polzik, E. S. Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 82, 1041–1093 (2010).
Phillips, D. F., Fleischhauer, A., Mair, A., Walsworth, R. L. & Lukin, M. D. Storage of light in atomic vapor. Phys. Rev. Lett. 86, 783–786 (2001).
Liu, C., Dutton, Z., Behroozi, C. H. & Hau, L. V. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 409, 490–493 (2001).
Bajcsy, M. et al. Efficient all-optical switching using slow light within a hollow fiber. Phys. Rev. Lett. 102, 203902 (2009).
Venkataraman, V., Saha, K., Londero, P. & Gaeta, A. L. Few-photon all-optical modulation in a photonic band-gap fiber. Phys. Rev. Lett. 107, 193902 (2011).
Nikoghosyan, G. & Fleischhauer, M. Photon-number selective group delay in cavity induced transparency. Phys. Rev. Lett. 105, 013601 (2010).
Chen, W. et al. All-optical switch and transistor gated by one stored photon. Science 341, 768–770 (2013).
Friedler, I., Petrosyan, D., Fleischhauer, M. & Kurizki, G. Long-range interactions and entanglement of slow single-photon pulses. Phys. Rev. A 72, 043803 (2005).
Moller, D., Madsen, L. B. & Molmer, K. Quantum gates and multiparticle entanglement by Rydberg excitation blockade and adiabatic passage. Phys. Rev. Lett. 100, 170504 (2008).
Rajapakse, R. M. et al. Single-photon nonlinearities using arrays of cold polar molecules. Phys. Rev. A 80, 013810 (2009).
Lukin, M. D. et al. Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 87, 037901 (2001).
Petrosyan, D., Otterbach, J. & Fleischhauer, M. Electromagnetically induced transparency with Rydberg atoms. Phys. Rev. Lett. 107, 213601 (2011).
Sevincli, S., Henkel, N., Ates, C. & Pohl, T. Nonlocal nonlinear optics in cold Rydberg gases. Phys. Rev. Lett. 107, 153001 (2011).
Muller, M., Lesanovsky, I., Weimer, H., Buchler, H. P. & Zoller, P. Mesoscopic Rydberg gate based on electromagnetically induced transparency. Phys. Rev. Lett. 102, 170502 (2009).
Pritchard, J. D. et al. Cooperative atom–light interaction in a blockaded Rydberg ensemble. Phys. Rev. Lett. 105, 193603 (2010).
Pritchard, J., Weatherill, K. & Adams, C. Nonlinear optics using cold Rydberg atoms in Annual Review of Cold Atoms and Molecules (eds Madison, K. W., Wang, Y., Rey, A. M. & Bongs, K.) 1, 301–350 (World Scientific, 2013).
Peyronel, T. et al. Quantum nonlinear optics with single photons enabled by strongly interacting atoms. Nature 488, 57–60 (2012).
Dudin, Y. O. & Kuzmich, A. Strongly interacting Rydberg excitations of a cold atomic gas. Science 336, 887–889 (2012).
Baur, S., Tiarks, D., Rempe, G. & Dürr, S. Single-photon switch based on Rydberg blockade. Phys. Rev. Lett. 112, 073901 (2014).
Li, L., Dudin, Y. O. & Kuzmich, A. Entanglement between light and an optical atomic excitation. Nature 498, 466–469 (2013).
Maxwell, D. et al. Storage and control of optical photons using Rydberg polaritons. Phys. Rev. Lett. 110, 103001 (2013).
Firstenberg, O. et al. Attractive photons in a quantum nonlinear medium. Nature 502, 71–75 (2013).
Lai, Y. & Haus, H. A. Quantum theory of solitons in optical fibers. II. Exact solution. Phys. Rev. A 40, 854–866 (1989).
Drummond, P. D., Shelby, R. M., Friberg, S. R. & Yamamoto, Y. Quantum solitons in optical fibres. Nature 365, 307–313 (1993).
Ritter, S. et al. An elementary quantum network of single atoms in optical cavities. Nature 484, 195–200 (2012).
Grangier, P., Levenson, J. A. & Poizat, J.-P. Quantum non-demolition measurements in optics. Nature 396, 537–542 (1998).
O'Shea, D., Junge, C., Volz, J. & Rauschenbeutel, A. Fiber-optical switch controlled by a single atom. Phys. Rev. Lett. 111, 193601 (2013).
Shomroni, I. et al. All-optical routing of single photons by a one-atom switch controlled by a single photon. Science http://dx.doi.org/10.1126/science.1254699 (2014).
Chang, D. E., Sørensen, A. S., Demler, E. A. & Lukin, M. D. A single-photon transistor using nanoscale surface plasmons. Nature Phys. 3, 807–812 (2007).
Law, C. K. & Eberly, J. H. Arbitrary control of a quantum electromagnetic field. Phys. Rev. Lett. 76, 1055–1058 (1996).
Plenio, M. B., Huelga, S. F., Beige, A. & Knight, P. L. Cavity-loss-induced generation of entangled atoms. Phys. Rev. A 59, 2468–2475 (1999).
Chiao, R. Y., Deutsch, I. H. & Garrison, J. C. Two-photon bound state in self-focusing media. Phys. Rev. Lett. 67, 1399–1402 (1991).
Deutsch, I. H., Chiao, R. Y. & Garrison, J. C. Two-photon bound states: The diphoton bullet in dispersive self-focusing media. Phys. Rev. A 47, 3330–3336 (1993).
Kheruntsyan, K. V. & Drummond, P. D. Three-dimensional quantum solitons with parametric coupling. Phys. Rev. A 58, 2488–2499 (1998).
Hartmann, M. J., Brandao, F. G. S. L. & Plenio, M. B. Strongly interacting polaritons in coupled arrays of cavities. Nature Phys. 2, 849–855 (2006).
Greentree, A. D., Tahan, C., Cole, J. H. & Hollenberg, L. C. L. Quantum phase transitions of light. Nature Phys. 2, 856–861 (2006).
Angelakis, D. G., Santos, M. F. & Bose, S. Photon-blockade-induced Mott transitions and spin models in coupled cavity arrays. Phys. Rev. A 76, 031805 (2007).
Carusotto, I. & Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 85, 299–366 (2013).
Chang, D. E. et al. Crystallization of strongly interacting photons in a nonlinear optical fibre. Nature Phys. 4, 884–889 (2008).
Otterbach, J., Moos, M., Muth, D. & Fleischhauer, M. Wigner crystallization of single photons in cold Rydberg ensembles. Phys. Rev. Lett. 111, 113001 (2013).
Carusotto, I. et al. Fermionized photons in an array of driven dissipative nonlinear cavities. Phys. Rev. Lett. 103, 033601 (2009).
Kiffner, M. & Hartmann, M. J. Dissipation-induced correlations in one-dimensional bosonic systems. New J. Phys. 13, 053027 10.1088/1367-2630/13/5/053027(2011).
Shen, J.-T. & Fan, S. Strongly correlated two-photon transport in a one-dimensional waveguide coupled to a two-level system. Phys. Rev. Lett. 98, 153003 (2007).
Shi, T. & Sun, C. P. Lehmann–Symanzik–Zimmermann reduction approach to multiphoton scattering in coupled-resonator arrays. Phys. Rev. B 79, 205111 (2009).
Pletyukhov, M. & Gritsev, V. Scattering of massless particles in one-dimensional chiral channel. New J. Phys. 14, 095028 10.1088/1367-2630/14/9/095028(2012).
Vetsch, E. et al. Optical interface created by laser-cooled atoms trapped in the evanescent field surrounding an optical nanofiber. Phys. Rev. Lett. 104, 203603 (2010).
Goban, A. et al. Atom–light interactions in photonic crystals. Nature Commun. 5, 3808 (2014).
Thompson, J. D. et al. Coupling a single trapped atom to a nanoscale optical cavity. Science 340, 1202–1205 (2013).
Volz, J., Scheucher, M., Junge, C. & Rauschenbeutel, A. Nonlinear phase shift for single fiber-guided photons interacting with a single atom. Preprint at http://lanl.arXiv.org/abs/1403.1860v1 (2014).
Akimov, A. V. et al. Generation of single optical plasmons in metallic nanowires coupled to quantum dots. Nature 450, 402–406 (2007).
Kolesov, R. et al. Wave–particle duality of single surface plasmon polaritons. Nature Phys. 5, 470–474 (2009).
Aspelmeyer, M., Groblacher, S., Hammerer, K. & Kiesel, N. Quantum optomechanics — throwing a glance. J. Opt. Soc. Am. B 27, A189–A197 (2010).
Rabl, P. Photon blockade effect in optomechanical systems. Phys. Rev. Lett. 107, 063601 (2011).
Chan, J., Safavi-Naeini, A. H., Hill, J. T., Meenehan, S. & Painter, O. Optimized optomechanical crystal cavity with acoustic radiation shield. Appl. Phys. Lett. 101, 081115 (2012).
Gupta, S., Moore, K. L., Murch, K. W. & Stamper-Kurn, D. M. Cavity nonlinear optics at low photon numbers from collective atomic motion. Phys. Rev. Lett. 99, 213601 (2007).
Gullans, M., Chang, D. E., Koppens, F. H. L., de Abajo, F. J. G. & Lukin, M. D. Single-photon nonlinear optics with graphene plasmons. Phys. Rev. Lett. 111, 247401 10.1103/PhysRevLett.111.247401(2013).
Acknowledgements
The authors acknowledge C. Adams, I. Cirac, W. Chen, Y. Chu, E. Demler, M. Fleischhauer, O. Firstenberg, S. Harris, V. Gritsev, A. Gorshkov, A. Imamoğlu, H. J. Kimble, N. de Leon, M. Loncar, H. Tanji-Suzuki, T. Peyronel, T. Pohl, G. Rempe, A. Sørensen, M. O. Scully, T. Tiecke, J. Thompson, J. Vuckovic, S. Yelin, A. Zibrov, and P. Zoller for the many discussions and contributions that resulted in the work described in this Review. Support from the National Science Foundation, Harvard-MIT Center for Ultracold Atoms, Defense Advanced Research Projects Agency, Air Force Office of Scientific Research Multidisciplinary University Research Initiative, Packard Foundation, and European project Graphene-Based Single-Photon Nonlinear Optical Devices (GRASP) is gratefully acknowledged. D.E.C. acknowledges support from Fundacio Privada Cellex Barcelona and the Ramon y Cajal programme.
Author information
Authors and Affiliations
Contributions
The authors contributed equally to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Chang, D., Vuletić, V. & Lukin, M. Quantum nonlinear optics — photon by photon. Nature Photon 8, 685–694 (2014). https://doi.org/10.1038/nphoton.2014.192
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2014.192
This article is cited by
-
Photon bound state dynamics from a single artificial atom
Nature Physics (2023)
-
Large scale purification in semiconductors using Rydberg excitons
Nature Communications (2023)
-
Quantum enhanced radio detection and ranging with solid spins
Nature Communications (2023)
-
Two electrons interacting at a mesoscopic beam splitter
Nature Nanotechnology (2023)
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)