Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

On the experimental verification of quantum complexity in linear optics

Nature Photonics volume 8, pages 621–626 (2014)Cite this article

Subjects

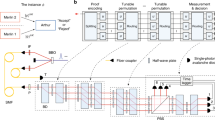
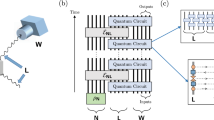
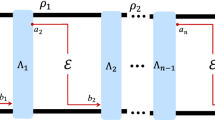
Abstract

Quantum computers promise to solve certain problems that are forever intractable to classical computers. The first of these devices are likely to tackle bespoke problems suited to their own particular physical capabilities. Sampling the probability distribution from many bosons interfering quantum-mechanically is conjectured to be intractable to a classical computer but solvable with photons in linear optics. However, the complexity of this type of problem means its solution is mathematically unverifiable, so the task of establishing successful operation becomes one of gathering sufficiently convincing circumstantial or experimental evidence. Here, we develop scalable methods to experimentally establish correct operation for this class of computation, which we implement for three, four and five photons in integrated optical circuits, on Hilbert spaces of up to 50,000 dimensions. Our broad approach is practical for all quantum computational architectures where formal verification methods for quantum algorithms are either intractable or unknown.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Experimental set-up to generate interfere and detect single photons.
Figure 2: Three-photon data from the RU chip showing verification of boson sampling against the uniform distribution and discrimination between quantum and classical statistics.
Figure 3: The absence and emergence of multimode correlations in the form of bosonic clouds in three-photon correlation cubes for a nine-mode RU and a 21-mode QW.
Figure 4: Experimental verification of correct sampling with bosonic clouding using a QW unitary.

References

  1. Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).

    Article  MathSciNet  Google Scholar 

  2. Barz, S., Fitzsimons, J. F., Kashefi, E. & Walther, P. Experimental verification of quantum computation. Nature Phys. 9, 727–731 (2013).

    Article  ADS  Google Scholar 

  3. Aspuru-Guzik, A. & Walther, P. Photonic quantum simulators. Nature Phys. 8, 285–291 (2012).

    Article  ADS  Google Scholar 

  4. Aaronson, S. & Arkhipov, A. in Proceedings of the 43rd Annual ACM Symposium on Theory of Computing, San Jose 333–342 (ACM Press, 2011).

    Google Scholar 

  5. Valiant, L. G. The complexity of computing the permanent. Theor. Comput. Sci. 8, 189–201 (1979).

    Article  MathSciNet  Google Scholar 

  6. Troyansky, L. & Tishby, N. in Proceedings of Physics and Computation (PhysComp 96) 314–318 (New England Complex Systems Institute, 1996).

  7. Scheel, S. in Quantum Information Processing Ch. 28 (Wiley, 2005).

  8. Peruzzo, A., Laing, A., Politi, A., Rudolph, T. & O'Brien, J. L. Multimode quantum interference of photons in multiport integrated devices. Nature Commun. 2, 224 (2011).

    Article  ADS  Google Scholar 

  9. Shor, P. W. in Proceedings of the 35th Annual Symposium on Foundations of Computer Science (ed. Goldwasser, S.) 124–134 (IEEE Press, 1994).

    Book  Google Scholar 

  10. Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2010).

    Book  Google Scholar 

  11. Broome, M. A. et al. Photonic boson sampling in a tunable circuit. Science 339, 794–798 (2013).

    Article  ADS  Google Scholar 

  12. Spring, J. B. et al. Boson sampling on a photonic chip. Science 339, 798–801 (2013).

    Article  ADS  Google Scholar 

  13. Crespi, A. et al. Integrated multimode interferometers with arbitrary designs for photonic boson sampling. Nature Photon. 7, 545–549 (2013).

    Article  ADS  Google Scholar 

  14. Tillmann, M. et al. Experimental boson sampling. Nature Photon. 7, 540–544 (2013).

    Article  ADS  Google Scholar 

  15. Reck, M., Zeilinger, A. Bernstein, H. J. & Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61 (1994).

    Article  ADS  Google Scholar 

  16. Matthews, J. C. F., Politi, A., Stefanov, A. & O'Brien, J. L. Manipulation of multiphoton entanglement in waveguide quantum circuits. Nature Photon. 3, 346–350 (2009).

    Article  ADS  Google Scholar 

  17. Shadbolt, P. J. et al. Generating, manipulating and measuring entanglement and mixture with a reconfigurable photonic circuit. Nature Photon. 6, 45–49 (2012).

    Article  ADS  Google Scholar 

  18. Lobino, M. et al. Complete characterization of quantum-optical processes. Science 322, 563–566 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  19. Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).

    Article  ADS  Google Scholar 

  20. Jerrum, M., Sinclair, A. & Vigoda, E. A polynomial-time approximation algorithm for the permanent of a matrix with nonnegative entries. J. Assoc. Comput. Mach. 51, 671–697 (2004).

    Article  MathSciNet  Google Scholar 

  21. Aaronson, S. & Arkhipov, A. Boson sampling is far from uniform. Preprint at http://lanl.arxiv.org/abs/1309.7460 (2013).

  22. Bromberg, Y., Lahini, Y., Morandotti, R. & Silberberg, Y. Quantum and classical correlations in waveguide lattices. Phys. Rev. Lett. 102, 253904 (2009).

    Article  ADS  Google Scholar 

  23. Peruzzo, A. et al. Quantum walks of correlated photons. Science 329, 1500–1503 (2010).

    Article  ADS  Google Scholar 

  24. Meinecke, J. D. A. et al. Coherent time evolution and boundary conditions of two-photon quantum walks in waveguide arrays. Phys. Rev. A 88, 012308 (2013).

    Article  ADS  Google Scholar 

  25. Matthews, J. C. F. et al. Observing fermionic statistics with photons in arbitrary processes. Sci. Rep. 3, 1539 10.1038/srep01539(2013).

    Article  Google Scholar 

  26. Sansoni, L. et al. Two-particle bosonic-fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108, 010502 (2012).

    Article  ADS  Google Scholar 

  27. Gogolin, C., Kliesch, M., Aolita, L. & Eisert, J. Boson-sampling in the light of sample complexity. Preprint at http://lanl.arxiv.org/abs/1306.3995 (2013).

  28. Laing, A. & O'Brien, J. L. Super-stable tomography of any linear optical device. Preprint at http://lanl.arxiv.org/abs/1208.2868 (2012).

  29. Arkhipov, A. & Kuperberg, G. The bosonic birthday paradox. Geom. Topol. Monog. 18, 1–7 (2012).

    Article  MathSciNet  Google Scholar 

  30. Spagnolo, N. et al. General rules for bosonic bunching in multimode interferometers. Phys. Rev. Lett. 111, 130503 (2013).

    Article  ADS  Google Scholar 

  31. Tanida, M., Okamoto, R. & Takeuchi, S. Highly indistinguishable heralded single-photon sources using parametric down conversion. Opt. Express 20, 15275–15285 (2012).

    Article  ADS  Google Scholar 

  32. Perets, H. B. et al. Realization of quantum walks with negligible decoherence in waveguide lattices. Phys. Rev. Lett. 100, 170506 (2008).

    Article  ADS  Google Scholar 

  33. Lund, A. P. et al. Boson sampling from Gaussian states. Preprint at http://lanl.arxiv.org/abs/1305.4346 (2013).

  34. Spagnolo, N. et al. Efficient experimental validation of photonic boson sampling against the uniform distribution. Preprint at http://lanl.arxiv.org/abs/1311.1622 (2013).

Download references

Acknowledgements

The authors acknowledge support from the Engineering and Physical Sciences Research Council (EPSRC), the European Research Council (ERC), the Centre for Nanoscience and Quantum Information (NSQI), the US Air Force Office of Scientific Research (AFOSR) and the US Army Research Laboratory (ARL) J.C.F.M. is supported by a Leverhulme Trust Early Career Fellowship. J.L.O.B. acknowledges a Royal Society Wolfson Merit Award and a Royal Academy of Engineering Chair in Emerging Technologies. The authors thank G. Marshall, E. Martín López, A. Peruzzo, A. Politi and A. Rubenok for technical assistance.

Author information

Authors and Affiliations

  1. H. H. Wills Physics Laboratory & Department of Electrical and Electronic Engineering, Centre for Quantum Photonics, University of Bristol, Merchant Venturers Building, Woodland Road, Bristol, BS8 1UB, UK

    Jacques Carolan, Jasmin D. A. Meinecke, Peter J. Shadbolt, Nicholas J. Russell, Mark G. Thompson, Jeremy L. O'Brien, Jonathan C. F. Matthews & Anthony Laing

  2. Integrated Optical Microsystems Group, MESA+ Institute for Nanotechnology, University of Twente, Enschede, The Netherlands

    Nur Ismail & Kerstin Wörhoff

  3. Institute for Mathematical Sciences, Imperial College London, London, SW7 2BW, UK

    Terry Rudolph

Authors
  1. Jacques Carolan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jasmin D. A. Meinecke
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Peter J. Shadbolt
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Nicholas J. Russell
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Nur Ismail
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Kerstin Wörhoff
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Terry Rudolph
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Mark G. Thompson
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Jeremy L. O'Brien
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Jonathan C. F. Matthews
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Anthony Laing
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Devices were fabricated by N.I. and K.W. All other authors contributed to the theory, experiments, analysis and writing of the manuscript.

Corresponding authors

Correspondence to Jonathan C. F. Matthews or Anthony Laing.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 496 kb)

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Carolan, J., Meinecke, J., Shadbolt, P. et al. On the experimental verification of quantum complexity in linear optics. Nature Photon 8, 621–626 (2014). https://doi.org/10.1038/nphoton.2014.152

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphoton.2014.152

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing