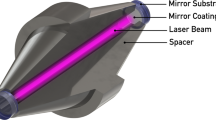
Abstract
Thermally induced fluctuations impose a fundamental limit on precision measurement. In optical interferometry, the current bounds of stability and sensitivity are dictated by the excess mechanical damping of the high-reflectivity coatings that comprise the cavity end mirrors. Over the last decade, the dissipation of these amorphous multilayer reflectors has at best been reduced by a factor of two. Here, we demonstrate a new paradigm in optical coating technology based on direct-bonded monocrystalline multilayers, which exhibit both intrinsically low mechanical loss and high optical quality. Employing these ‘crystalline coatings’ as end mirrors in a Fabry–Pérot cavity, we obtain a finesse of 150,000. More importantly, at room temperature, we observe a thermally limited noise floor consistent with a tenfold reduction in mechanical damping when compared with the best dielectric multilayers. These results pave the way for the next generation of ultra-sensitive interferometers, as well as for new levels of laser stability.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Schiller, S. et al. Experimental limits for low-frequency space–time fluctuations from ultrastable optical resonators. Phys. Rev. D 69, 027504 (2004).
Ludlow, A. D. et al. Sr lattice clock at 1×10−16 fractional uncertainty by remote optical evaluation with a Ca clock. Science 319, 1805–1808 (2008).
Rosenband, T. et al. Frequency ratio of Al+ and Hg+ single-ion optical clocks; metrology at the 17th decimal place. Science 319, 1808–1812 (2008).
Abbott, B. P. et al. LIGO: the laser interferometer gravitational wave observatory. Rep. Prog. Phys. 72, 076901 (2009).
Saulson, P. R. Thermal noise in mechanical experiments. Phys. Rev. D 42, 2437–2445 (1990).
Young, B. C., Cruz, F. C., Itano, W. M. & Bergquist, J. C. Visible lasers with subhertz linewidths. Phys. Rev. Lett. 82, 3799–3802 (1999).
Ludlow, A. D. et al. Compact, thermal-noise-limited optical cavity for diode laser stabilization at 1×10−15. Opt. Lett. 32, 641–643 (2007).
Millo, J. et al. Ultrastable lasers based on vibration insensitive cavities. Phys. Rev. A 79, 053829 (2009).
Jiang, Y. Y. et al. Making optical atomic clocks more stable with 10−16-level laser stabilization. Nature Photon. 5, 158–161 (2011).
Kessler, T. et al. A sub-40-mHz-linewidth laser based on a silicon single-crystal optical cavity. Nature Photon. 6, 687–692 (2012).
Nicholson, T. L. et al. Comparison of two independent Sr optical clocks with 1×10−17 stability at 103 s. Phys. Rev. Lett. 109, 230801 (2012).
Martin, M. J. et al. A quantum many-body spin system in an optical lattice clock. Science (in the press); preprint at http://lanl.arxiv.org/abs/1212.6291 (2013).
Numata, K., Kemery, A. & Camp, J. Thermal-noise limit in the frequency stabilization of lasers with rigid cavities. Phys. Rev. Lett. 93, 250602 (2004).
Bishof, M., Zhang, X., Martin, M. J. & Ye, J. An optical spectrum analyzer with quantum limited noise floor. Preprint at http://lanl.arxiv.org/abs/1303.6741 (2013).
Callen, H. B. & Welton, T. A. Irreversibility and generalized noise. Phys. Rev. 83, 34–40 (1951).
Landau, L. D. & Lifshitz, E. M. in Statistical Physics Ch. XII (Elsevier, 1996).
Harry, G. M. et al. Titania-doped tantala/silica coatings for gravitational wave detection. Class. Quant. Grav. 24, 405–416 (2007).
Iga, K. Surface-emitting laser—its birth and generation of new optoelectronics field. IEEE J. Sel. Top. Quant. 6, 1201–1215 (2000).
Aspelmeyer, M., Meystre, P. & Schwab, K. Quantum optomechanics. Phys. Today 65, 29–35 (2012).
Madsen, M. et al. Nanoscale semiconductor ‘X’ on substrate ‘Y’—processes, devices, and applications. Adv. Mater. 23, 3115–3127 (2011).
Rempe, G., Thompson, R. J., Kimble, H. J. & Lalezari, R. Measurement of ultralow losses in an optical interferometer. Opt. Lett. 17, 363–365 (1992).
Crooks, D. R. M. et al. Excess mechanical loss associated with dielectric mirror coatings on test masses in interferometric gravitational wave detectors. Class. Quant. Grav. 19, 883–896 (2002).
Harry, G. M. et al. Thermal noise in interferometric gravitational wave detectors due to dielectric optical coatings. Class. Quant. Grav. 19, 897–918 (2002).
Penn, S. D. et al. Mechanical loss in tantala/silica dielectric mirror coatings. Class. Quant. Grav. 20, 2917–2928 (2003).
Harry, G., Bodiya, T. & DeSalvo, R. in Gravitational Wave Detection (eds Ottaway, D. J. & Penn, S. D.) Ch. 14, 222 (Cambridge Univ. Press, 2012).
Braginsky, V. B., Gorodetsky, M. L. & Vyatchanin, S. P. Thermodynamical fluctuations and photo-thermal shot noise in gravitational wave antennae. Phys. Lett. A 264, 1–10 (1999).
Braginsky, V. B., Gorodetsky, M. L. & Vyatchanin, S. P. Thermo-refractive noise in gravitational wave antennae. Phys. Lett. A 271, 303–307 (2000).
Evans, M. et al. Thermo-optic noise in coated mirrors for high-precision optical measurements. Phys. Rev. D 78, 102003 (2008).
Gorodetsky, M. L. Thermal noises and noise compensation in high-reflection multilayer coating. Phys. Lett. A 372, 6813–6822 (2008).
Penn, S. D. et al. Frequency and surface dependence of the mechanical loss in fused silica. Phys. Lett. A 352, 3–6 (2006).
Amairi, S. et al. Reducing the effect of thermal noise in optical cavities. Appl. Phys. B http://dx.doi.org/10.1007/S00340-013-5464-8 (2013).
Bondarescu, M., Kogan, O. & Chen, Y. Optimal light beams and mirror shapes for future LIGO interferometers. Phys. Rev. D 78, 082002 (2008).
Kimble, H. J., Lev, B. L. & Ye, J. Optical interferometers with reduced sensitivity to thermal noise. Phys. Rev. Lett. 101, 260602 (2008).
Friedrich, D. et al. Waveguide grating mirror in a fully suspended 10 meter Fabry–Perot cavity. Opt. Express 19, 14955–14963 (2011).
Kemiktarak, U., Metcalfe, M., Durand, M. & Lawall, J. Mechanically compliant grating reflectors for optomechanics. Appl. Phys. Lett. 100, 061124 (2012).
Alnis, J. et al. Thermal-noise-limited crystalline whispering-gallery-mode resonator for laser stabilization. Phys. Rev. A 84, 011804 (2011).
Cole, G. D., Gröblacher, S., Gugler, K., Gigan, S. & Aspelmeyer, M. Monocrystalline AlxGa1–xAs heterostructures for high-reflectivity high-Q micromechanical resonators in the megahertz regime. Appl. Phys. Lett. 92, 261108 (2008).
Cole, G. D. in Proc. SPIE 8458, Optics & Photonics, Optical Trapping and Optical Micromanipulation IX, 8458–07 (SPIE, 2012).
Jewell, J. L., Scherer, A., McCall, S. L., Gossard, A. C. & English, J. H. GaAs–AlAs monolithic microresonator arrays. Appl. Phys. Lett. 51, 94–96 (1987).
Gröblacher, S., Gigan, S., Böhm, H. R., Zeilinger, A. & Aspelmeyer, M. Radiation-pressure self-cooling of a micromirror in a cryogenic environment. Europhys. Lett. 81, 54003 (2008).
Black, A. et al. Wafer fusion: materials issues and device results. IEEE J. Sel. Top. Quant. 3, 943–951 (1997).
Bai, Y., Cole, G. D., Bulsara, M. T. & Fitzgerald, E. A. Fabrication of GaAs-on-insulator via low temperature wafer bonding and sacrificial etching of Ge by XeF2 . J. Electrochem. Soc. 159, H183–H190 (2012).
Konagai, M., Sugimoto, M. & Takahashi, K. High efficiency GaAs thin film solar cells by peeled film technology. J. Cryst. Growth 45, 277–280 (1978).
Yablonovitch, E., Hwang, D. M., Gmitter, T. J., Florez, L. T. & Harbison, J. P. Van der Waals bonding of GaAs epitaxial liftoff films onto arbitrary substrates. Appl. Phys. Lett. 56, 2419–2421 (1990).
Notcutt, M. et al. Contribution of thermal noise to frequency stability of rigid optical cavity via hertz-linewidth lasers. Phys. Rev. A 73, 031804 (2006).
Schibli, T. et al. Optical frequency comb with submillihertz linewidth and more than 10 W average power. Nature Photon. 2, 355–359 (2008).
Benko, C. et al. Full phase stabilization of a Yb:fiber femtosecond frequency comb via high-bandwidth transducers. Opt. Lett. 37, 2196–2198 (2012).
Yamamoto, K. et al. Measurement of the mechanical loss of a cooled reflective coating for gravitational wave detection. Phys. Rev. D 74, 022002 (2006).
Knigge, A., Zorn, M., Wenzel, H., Weyers, M. & Trankle, C. High efficiency AlGaInP-based 650 nm vertical-cavity surface-emitting lasers. Electron. Lett. 37, 1222–1223 (2001).
Spitzer, W. G. & Whelan, J. M. Infrared absorption and electron effective mass in n-type gallium arsenide. Phys. Rev. 114, 59–63 (1959).
Acknowledgements
The authors thank M.R. Abernathy, R.X. Adhikari, A. Alexandrovski, C. Benko, T. Chalermsongsak, G.M. Harry, R. Lalezari, L-S. Ma, E. Murphy, M. Notcutt, S.D. Penn, A. Peters, P. Ullmann and R. Yanka for discussions and technical assistance. Work at the University of Vienna is supported by the Austrian Science Fund (FWF), the European Commission and the European Research Council (ERC) Starting Grant Program. The work at CMS is supported by the Austria Wirtschaftsservice GmbH (AWS) and the ERC Proof of Concept Initiative. Work at JILA is supported by the US National Institute of Standards and Technology (NIST), the DARPA QuASAR Program, and the US National Science Foundation (NSF) Physics Frontier Center at JILA. Microfabrication was carried out at the Center for Micro- and Nanostructures (ZMNS) of the Vienna University of Technology.
Author information
Authors and Affiliations
Contributions
G.D.C. and M.A. designed the epitaxial multilayer, developed the substrate transfer process, and fabricated the bonded mirror assemblies. W.Z., M.J.M. and J.Y. designed and characterized the optical cavity, performed the laser frequency noise and stability measurements, and analysed the data. All authors contributed to writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
G.D.C. and M.A. are co-founders of a startup company (Crystalline Mirror Solutions) and co-inventors on an international patent (European Application 11010091.4) focusing on the bonded mirror technology described in the Article.
Supplementary information
Supplementary information
Supplementary information (PDF 833 kb)
Rights and permissions
About this article
Cite this article
Cole, G., Zhang, W., Martin, M. et al. Tenfold reduction of Brownian noise in high-reflectivity optical coatings. Nature Photon 7, 644–650 (2013). https://doi.org/10.1038/nphoton.2013.174
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphoton.2013.174
This article is cited by
-
Experimental realization of a 12,000-finesse laser cavity based on a low-noise microstructured mirror
Communications Physics (2023)
-
Mid-infrared supermirrors with finesse exceeding 400 000
Nature Communications (2023)
-
Strained crystalline nanomechanical resonators with quality factors above 10 billion
Nature Physics (2022)
-
Transportable 30 cm optical cavity based ultrastable lasers with beating instability of \(2\times 10^{-16}\)
Applied Physics B (2022)
-
Crystallization behavior of ion beam sputtered HfO2 thin films and its effect on the laser-induced damage threshold
Journal of the European Optical Society-Rapid Publications (2021)