Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Strain-induced pseudomagnetic field and photonic Landau levels in dielectric structures

Nature Photonics volume 7, pages 153–158 (2013)Cite this article

Subjects

Abstract

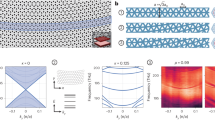
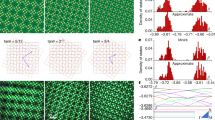
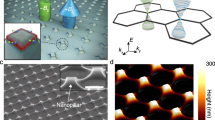
Magnetic effects at optical frequencies are notoriously weak, so magneto-optical devices must be large to create a sufficient effect. In graphene, it has been shown that inhomogeneous strains can induce ‘pseudomagnetic fields’ that behave in a similar manner to real ones. Here, we show experimentally and theoretically that it is possible to induce such a field at optical frequencies in a photonic lattice. To our knowledge, this is the first realization of a pseudomagnetic field in optics. The field yields ‘photonic Landau levels’ separated by bandgaps in the spatial spectrum of the structured dielectric lattice. The gaps between these highly degenerate levels lead to transverse optical confinement. The use of strain allows for the exploration of magnetic-like effects in a non-resonant way that would be otherwise inaccessible in optics. It also suggests the possibility that aperiodic photonic-crystal structures can achieve greater field enhancement and slow-light effects than periodic structures via high density of states at the Landau levels. Generalizing these concepts to systems beyond optics, such as matter waves in optical potentials, offers new intriguing physics that is fundamentally different from that in purely periodic structures.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Description of honeycomb photonic lattice and band structure.
Figure 2: Effect of strain on the eigenvalue spectrum of the honeycomb photonic lattice.
Figure 3: Experimental and simulation results for increasing strain.
Figure 4: Effect of a defect waveguide on beam confinement.

Similar content being viewed by others

References

  1. Haldane, F. D. M. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008).

    Article  ADS  Google Scholar 

  2. Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).

    Article  ADS  Google Scholar 

  3. Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nature Phys. 7, 907–912 (2011).

    Article  ADS  Google Scholar 

  4. Yariv, A., Xu, Y., Lee, R. K. & Scherer, A. Coupled-resonator optical waveguide: a proposal and analysis. Opt. Lett. 24, 711–713 (1999).

    Article  ADS  Google Scholar 

  5. Cai, W. & Shalaev, V. Optical Metamaterials: Fundamentals and Applications (Springer, 2009).

    Google Scholar 

  6. Plum, E. et al. Metamaterials: optical activity without chirality. Phys. Rev. Lett. 102, 113902 (2009).

    Article  ADS  Google Scholar 

  7. Kane, C. L. & Mele, E. J. Size, shape, and low energy electronic structure of carbon nanotubes. Phys. Rev. Lett. 78, 1932–1935 (1997).

    Article  ADS  Google Scholar 

  8. Guinea, F., Katsnelson, M. I. & Geim, A. K. Energy gaps and a zero-field quantum Hall effect in graphene by strain engineering. Nature Phys. 6, 30–33 (2010).

    Article  ADS  Google Scholar 

  9. Peleg, O. et al. Conical diffraction and gap solitons in honeycomb photonic lattices. Phys. Rev. Lett. 98, 103901 (2007).

    Article  ADS  Google Scholar 

  10. Bahat-Treidel, O., Peleg, O. & Segev, M. Symmetry breaking in honeycomb photonic lattices. Opt. Lett. 33, 2251–2253 (2008).

    Article  ADS  Google Scholar 

  11. Bahat-Treidel, O. & Segev, M. Nonlinear wave dynamics in honeycomb lattices. Phys. Rev. A 84, 021802(R) (2011).

    Article  ADS  Google Scholar 

  12. Szameit, A., Rechtsman, M. C., Bahat-Treidel, O. & Segev, M. PT-symmetry in honeycomb photonic lattices. Phys. Rev. A 84, 021806(R) (2011).

  13. Ablowitz, M. J., Nixon, S. D. & Zhu, Y. Conical diffraction in honeycomb lattices. Phys. Rev. A 79, 053830 (2009).

    Article  ADS  Google Scholar 

  14. Soljačić, M. & Joannopoulos, J. D. Enhancement of nonlinear effects using photonic crystals. Nature Mater. 3, 211–219 (2004).

    Article  ADS  Google Scholar 

  15. Molina, M. I. & Kivshar, Y. S. Discrete and surface solitons in photonic graphene nanoribbons. Opt. Lett. 35, 2895–2897 (2010).

    Article  ADS  Google Scholar 

  16. Birks, T. A., Knight, J. C. & Russell, P. S. J. Endlessly single-mode photonic crystal fiber. Opt. Lett. 22, 961–963 (1997).

    Article  ADS  Google Scholar 

  17. Christodoulides, D. N. & Joseph, R. I. Discrete self-focusing in nonlinear arrays of coupled waveguides. Opt. Lett. 13, 794–796 (1988).

    Article  ADS  Google Scholar 

  18. Fleischer, J. W., Segev, M., Efremidis, N. K. & Christodoulides, D. N. Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices. Nature 422, 147–150 (2003).

    Article  ADS  Google Scholar 

  19. Eisenberg, H. S., Silberberg, Y., Morandotti, R., Boyd, A. R. & Aitchison, J. S. Discrete spatial optical solitons in waveguide arrays. Phys. Rev. Lett. 81, 3383–3386 (1998).

    Article  ADS  Google Scholar 

  20. Lederer, F. et al. Discrete solitons in optics. Phys. Rep. 463, 1–126 (2008).

    Article  ADS  Google Scholar 

  21. Schwartz, T., Bartal, G., Fishman, S. & Segev, M. Transport and Anderson localization in disordered two-dimensional photonic lattices. Nature 446, 52–55 (2007).

    Article  ADS  Google Scholar 

  22. Makris, K. G., Suntsov, S., Christodoulides, D. N., Stegeman, G. I. & Hache, A. Discrete surface solitons. Opt. Lett. 30, 2466–2468 (2005).

    Article  ADS  Google Scholar 

  23. Malkova, N., Hromada, I., Wang, X., Bryant, G. & Chen, Z. Observation of optical Shockley-like surface states in photonic superlattices. Opt. Lett. 34, 1633–1635 (2009).

    Article  ADS  Google Scholar 

  24. Longhi, S. Quantum-optical analogies using photonic structures. Laser Photon. Rev. 3, 243–261 (2009).

    Article  ADS  Google Scholar 

  25. Szameit, A. & Nolte, S. Discrete optics in femtosecond-laser-written photonic structures. J. Phys. B 43, 163001 (2010).

    Article  ADS  Google Scholar 

  26. Bahat-Treidel, O. et al. Klein tunneling in deformed honeycomb lattices. Phys. Rev. Lett. 104, 063901 (2010).

    Article  ADS  Google Scholar 

  27. Sepkhanov, R. A., Bazaliy, Y. B. & Beenakker, C. W. J. Extremal transmission at the Dirac point of a photonic band structure. Phys. Rev. A 75, 063813 (2007).

    Article  ADS  Google Scholar 

  28. Bravo-Abad, J., Joannopoulos, J. D. & Soljačić, M. Enabling single-mode behavior over large areas with photonic Dirac cones. Proc. Natl Acad. Sci. USA 109, 9761–9765 (2012).

    Article  ADS  Google Scholar 

  29. Yu, Z. & Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nature Photon. 3, 91–94 (2009).

    Article  ADS  Google Scholar 

  30. Stone, M. Quantum Hall Effect (World Scientific, 1992).

    Book  Google Scholar 

  31. Kohmoto, M. & Hasegawa, Y. Zero modes and edge states of the honeycomb lattice. Phys. Rev. B 76, 205402 (2007).

    Article  ADS  Google Scholar 

  32. Lodahl, P. et al. Controlling the dynamics of spontaneous emission from quantum dots by photonic crystals. Nature 430, 654–657 (2004).

    Article  ADS  Google Scholar 

  33. Johnson, S. G., Fan, S., Villeneuve, P. R., Joannopoulos, J. D. & Kolodziejski, L. A. Guided modes in photonic crystal slabs. Phys. Rev. B 60, 5751–5758 (1999).

    Article  ADS  Google Scholar 

  34. Purcell, E. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69, 681 (1946).

    Article  Google Scholar 

  35. Akhmerov, A. R. & Beenakker, C. W. J. Boundary conditions for Dirac fermions on a terminated honeycomb lattice. Phys. Rev. B 77, 085423 (2008).

    Article  ADS  Google Scholar 

  36. Ruter, C. E. et al. Observation of parity-time symmetry in optics. Nature Phys. 6, 192–195 (2010).

    Article  ADS  Google Scholar 

  37. Guo, A. et al. Observation of PT-symmetry breaking in complex optical potentials. Phys. Rev. Lett. 103, 093902 (2009).

    Article  ADS  Google Scholar 

  38. Kottos, T. Optical physics: broken symmetry makes light work. Nature Phys. 6, 166–167 (2010).

    Article  ADS  Google Scholar 

  39. Makris, K. G., El-Ganainy, R., Christodoulides, D. N. & Musslimani, Z. H. Beam dynamics in PT symmetric optical lattices. Phys. Rev. Lett. 100, 103904 (2008).

    Article  ADS  Google Scholar 

  40. Klaiman, S., Günther, U. & Moiseyev, N. Visualization of branch points in PT-symmetric waveguides. Phys. Rev. Lett. 101, 080402 (2008).

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

M.C.R. acknowledges the Azrieli Foundation for the award of an Azrieli fellowship. A.S. acknowledges support from the German Ministry of Education and Research (Center for Innovation Competence programme, grant 03Z1HN31). M.S. acknowledges support from the Israel Science Foundation, the USA–Israel Binational Science Foundation, and the Advanced Grant by the European Research Council.

Author information

Author notes

  1. Mikael C. Rechtsman and Julia M. Zeuner: These authors contributed equally to this work

Authors and Affiliations

  1. Physics Department, Technion–Israel Institute of Technology, Haifa, 32000, Israel

    Mikael C. Rechtsman & Mordechai Segev

  2. Institute of Applied Physics, Abbe Center of Photonics, Friedrich-Schiller-Universität Jena, Max-Wien-Platz 1, 07743, Jena, Germany

    Julia M. Zeuner, Andreas Tünnermann, Stefan Nolte & Alexander Szameit

Authors
  1. Mikael C. Rechtsman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Julia M. Zeuner
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Andreas Tünnermann
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Stefan Nolte
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mordechai Segev
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Alexander Szameit
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

M.C.R. and J.M.Z. contributed equally. All authors contributed significantly.

Corresponding author

Correspondence to Mikael C. Rechtsman.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary information

Supplementary information (PDF 1138 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rechtsman, M., Zeuner, J., Tünnermann, A. et al. Strain-induced pseudomagnetic field and photonic Landau levels in dielectric structures. Nature Photon 7, 153–158 (2013). https://doi.org/10.1038/nphoton.2012.302

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphoton.2012.302

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing