Abstract
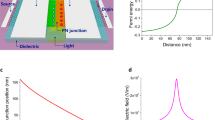
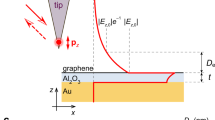
Terahertz (THz) fields are widely used for sensing, communication and quality control1. In future applications, they could be efficiently confined, enhanced and manipulated well below the classical diffraction limit through the excitation of graphene plasmons (GPs)2,3. These possibilities emerge from the strongly reduced GP wavelength, λp, compared with the photon wavelength, λ0, which can be controlled by modulating the carrier density of graphene via electrical gating4,5,6,7,8. Recently, GPs in a graphene/insulator/metal configuration have been predicted to exhibit a linear dispersion (thus called acoustic plasmons) and a further reduced wavelength, implying an improved field confinement9,10,11, analogous to plasmons in two-dimensional electron gases (2DEGs) near conductive substrates12. Although infrared GPs have been visualized by scattering-type scanning near-field optical microscopy (s-SNOM)6,7, the real-space imaging of strongly confined THz plasmons in graphene and 2DEGs has been elusive so far—only GPs with nearly free-space wavelengths have been observed13. Here we demonstrate real-space imaging of acoustic THz plasmons in a graphene photodetector with split-gate architecture. To that end, we introduce nanoscale-resolved THz photocurrent near-field microscopy, where near-field excited GPs are detected thermoelectrically14 rather than optically6,7. This on-chip detection simplifies GP imaging as sophisticated s-SNOM detection schemes can be avoided. The photocurrent images reveal strongly reduced GP wavelengths (λp ≈ λ0/66), a linear dispersion resulting from the coupling of GPs with the metal gate below the graphene, and that plasmon damping at positive carrier densities is dominated by Coulomb impurity scattering.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Tonouchi, M. Cutting-edge terahertz technology. Nat. Photon. 1, 97–105 (2007).
Wunsch, B., Stauber, T., Sols, F. & Guinea, F. Dynamical polarization of graphene at finite doping. New J. Phys. 8, 318 (2006).
Jablan, M., Buljan, H. & Soljačić, M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 80, 245435 (2009).
Ju, L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotech. 6, 630–634 (2011).
Yan, H. et al. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat. Nanotech. 7, 330–334 (2012).
Chen, J. et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 487, 77–81 (2012).
Fei, Z. et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 487, 82–85 (2012).
Alonso-González, P. et al. Controlling graphene plasmons with resonant metal antennas and spatial conductivity patterns. Science 344, 1369–1373 (2014).
Stauber, T. & Gomez-Santos, G. Plasmons in layered structures including graphene. New J. Phys. 14, 105018 (2012).
Gu, X., Lin, I.-T. & Liu, J.-M. Extremely confined terahertz surface plasmon-polaritons in graphene-metal structures. Appl. Phys. Lett. 103, 071103 (2013).
Principi, A., Asgari, R. & Polini, M. Acoustic plasmons and composite hole-acoustic plasmon satellite bands in graphene on a metal gate. Solid State Commun. 151, 1627–1630 (2011).
Allen, S. J., Tsui, D. C. & Logan, R. A. Observation of the two-dimensional plasmon in silicon inversion layers. Phys. Rev. Lett. 38, 980–983 (1977).
Mitrofanov, O. et al. Terahertz near-field imaging of surface plasmon waves in graphene structures. Solid State Commun. 224, 47–52 (2015).
Lundeberg, M. B. et al. Thermoelectric detection and imaging of propagating graphene plasmons. http://dx.doi.org/10.1038/nmat4755 (2016).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Huber, A. J., Keilmann, F., Wittborn, J., Aizpurua, J. & Hillenbrand, R. Terahertz near-field nanoscopy of mobile carriers in single semiconductor nanodevices. Nano Lett. 8, 3766–3770 (2008).
Woessner, A. et al. Near-field photocurrent nanoscopy on bare and encapsulated graphene. Nat. Commun. 7, 10783 (2016).
Keilmann, F. & Hillenbrand, R. Near-field microscopy by elastic light scattering from a tip. Phil. Trans. R. Soc. Lond. A 362, 787–805 (2004).
Gabor, N. M. et al. Hot carrier–assisted intrinsic photoresponse in graphene. Science 334, 648–652 (2011).
Cai, X. et al. Sensitive room-temperature terahertz detection via the photothermoelectric effect in graphene. Nat. Nanotech. 9, 814–819 (2014).
Diaconescu, B. et al. Low-energy acoustic plasmons at metal surfaces. Nature 448, 57–59 (2007).
Koppens, F. H. L., Chang, D. E. & García de Abajo, F. J. Graphene plasmonics: a platform for strong light–matter interactions. Nano Lett. 11, 3370–3377 (2011).
Nikitin, A. Y., Guinea, F., Garcia-Vidal, F. J. & Martin-Moreno, L. Fields radiated by a nanoemitter in a graphene sheet. Phys. Rev. B 84, 195446 (2011).
Christensen, J., Manjavacas, A., Thongrattanasiri, S., Koppens, F. H. L. & García de Abajo, F. J. Graphene plasmon waveguiding and hybridization in individual and paired nanoribbons. ACS Nano 6, 431–440 (2012).
Profumo, R. E. V., Asgari, R., Polini, M. & MacDonald, A. H. Double-layer graphene and topological insulator thin-film plasmons. Phys. Rev. B 85, 085443 (2012).
Shung, K. W. K. Dielectric function and plasmon structure of stage-1 intercalated graphite. Phys. Rev. B 34, 979–993 (1986).
Vafek, O. Thermoplasma polariton within scaling theory of single-layer graphene. Phys. Rev. Lett. 97, 266406 (2006).
Falkovsky, L. A. & Varlamov, A. A. Space-time dispersion of graphene conductivity. Eur. Phys. J. B 56, 281–284 (2007).
Woessner, A. et al. Highly confined low-loss plasmons in graphene–boron nitride heterostructures. Nat. Mater. 14, 421–425 (2015).
Principi, A. et al. Plasmon losses due to electron-phonon scattering: the case of graphene encapsulated in hexagonal boron nitride. Phys. Rev. B 90, 165408 (2014).
Principi, A., Vignale, G., Carrega, M. & Polini, M. Impact of disorder on Dirac plasmon losses. Phys. Rev. B 88, 121405 (2013).
Cai, Y., Zhang, L., Zeng, Q., Cheng, L. & Xu, Y. Infrared reflectance spectrum of BN calculated from first principles. Solid State Commun. 141, 262–266 (2007).
Caldwell, J. D. et al. Sub-diffractional volume-confined polaritons in the natural hyperbolic material hexagonal boron nitride. Nat. Commun. 5, 5221 (2014).
Acknowledgements
We thank C. Crespo for technical assistance with the THz laser. R.H., P.A-G. and A.N. acknowledge support from the Spanish Ministry of Economy and Competitiveness (national projects MAT2015-65525-R, FIS2014-60195-JIN and MAT2014-53432-C5-4-R, respectively). F.H.L.K. acknowledges support from the Fundacio Cellex Barcelona, the ERC Career integration grant (294056, GRANOP), the ERC starting grant (307806, CarbonLight), the Government of Catalonia through the SGR grant (2014-SGR-1535), the Mineco grants Ramón y Cajal (RYC-2012-12281) and Plan Nacional (FIS2013-47161-P) and project GRASP (FP7-ICT-2013-613024-GRASP). R.H., F.H.L.K., A.P. and M.P. acknowledge support by the EC under the Graphene Flagship (contract no. CNECT-ICT-604391). Y.G. and J.H. acknowledge support from the US Office of Naval Research (N00014-13-1- 0662).
Author information
Authors and Affiliations
Contributions
P.A-G., A.J.H. and R.H. implemented the THz photocurrent near-field microscope. P.A-G. and A.W. performed the photocurrent nanoscopy experiments. A.Y.N. and A.W. performed the simulations of the GP near-field distributions and GP dispersion. Y.G. fabricated the h-BN/graphene/h-BN photodetector devices. A.P., N.F. and M.P. developed the analytic model for the acoustic GP dispersion and the theory of plasmon damping. W.Y. and S.V. fabricated photocurrent devices based on exfoliated and CVD-grown graphene. K.W. and T.T. synthesized the h-BN. F.C., L.E.H. and J.H. coordinated the fabrication of the different photocurrent samples. P.A-G., A.Y.N., A.W., M.B.L., M.P., F.H.L.M. and R.H. analysed the data. P.A-G., A.Y.N. and R.H. wrote the manuscript with input from all authors. All authors contributed to the scientific discussion and manuscript revisions.
Corresponding authors
Ethics declarations
Competing interests
R.H. is a co-founder of Neaspec GmbH, a company producing scattering-type scanning near-field optical microscope systems such as the one used in this study. All other authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1355 kb)
Rights and permissions
About this article
Cite this article
Alonso-González, P., Nikitin, A., Gao, Y. et al. Acoustic terahertz graphene plasmons revealed by photocurrent nanoscopy. Nature Nanotech 12, 31–35 (2017). https://doi.org/10.1038/nnano.2016.185
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nnano.2016.185
This article is cited by
-
Near-field detection of gate-tunable anisotropic plasmon polaritons in black phosphorus at terahertz frequencies
Nature Communications (2024)
-
Terahertz microscopy using laser feedback interferometry based on a generalised phase-stepping algorithm
Scientific Reports (2024)
-
Real-space observation of ultraconfined in-plane anisotropic acoustic terahertz plasmon polaritons
Nature Materials (2023)
-
Photocurrent as a multiphysics diagnostic of quantum materials
Nature Reviews Physics (2023)
-
Relaxing Graphene Plasmon Excitation Constraints Through the Use of an Epsilon-Near-Zero Substrate
Plasmonics (2023)