Abstract
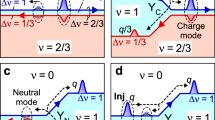
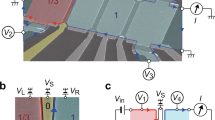
The model of interacting fermion systems in one dimension known as a Tomonaga–Luttinger liquid (TLL)1,2 provides a simple and exactly solvable theoretical framework that predicts various intriguing physical properties. Evidence of a TLL has been observed as power-law behaviour in electronic transport on various types of one-dimensional conductor3,4,5. However, these measurements, which rely on d.c. transport involving electron tunneling processes, cannot identify the long-awaited hallmark of charge fractionalization, in which an injection of elementary charge e from a non-interacting lead is divided into the non-trivial effective charge e* and the remainder, e−e* (refs 6, 7, 8). Here, we report time-resolved transport measurements9 on an artificial TLL composed of coupled integer quantum Hall edge channels10, in which we successfully identify single charge fractionalization processes. A wave packet of charge q incident from a non-interacting region breaks up into several fractionalized charge wave packets at the edges of the artificial TLL, from which transport eigenmodes can be evaluated directly. These results are informative for elucidating the nature of TLLs and low-energy excitations in the edge channels11.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Tomonaga, S. Remarks on Bloch's method of sound waves applied to many-fermion problems. Prog. Theor. Phys. 5, 544–569 (1950).
Luttinger, J. M. An exactly soluble model of a many-fermion system. J. Math. Phys. 4, 1154–1162 (1963).
Tarucha, S., Honda, T. & Saku, T. Reduction of quantized conductance at low temperatures observed in 2 to 10 µm-long quantum wires. Solid State Commun. 94, 413–418 (1995).
Bockrath, M. et al. Luttinger-liquid behaviour in carbon nanotubes. Nature 397, 598–601 (1999).
Grayson, M., Tsui, D. C., Pfeiffer, L. N., West, K. W. & Chang, A. M. Continuum of chiral Luttinger liquids at the fractional quantum Hall edge. Phys. Rev. Lett. 80, 1062–1065 (1998).
Safi, I. & Schulz, H. J. Transport in an inhomogeneous interacting one-dimensional system. Phys. Rev. B 52, R17040–R17043 (1995).
Pham, K-V., Gabay, M. & Lederer, P. Fractional excitations in the Luttinger liquid. Phys. Rev. B 61, 16397–16422 (2000).
Imura, K-I., Pham, K-V., Lederer, P. & Piéchon, F. Conductance of one-dimensional quantum wires. Phys. Rev. B 66, 035313 (2002).
Kamata, H., Ota, T., Muraki, K. & Fujisawa, T. Voltage-controlled group velocity of edge magnetoplasmon in the quantum Hall regime. Phys. Rev. B 81, 085329 (2010).
Berg, E., Oreg, Y., Kim, E-A. & von Oppen, F. Fractional charges on an integer quantum Hall edge. Phys. Rev. Lett. 102, 236402 (2009).
Venkatachalam, V., Hart, S., Pfeiffer, L., West, K. & Yacoby, A. Local thermometry of neutral modes on the quantum Hall edge. Nature Phys. 8, 676–681 (2012).
Van Wees, B. J. et al. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 60, 848–850 (1988).
Kane, C. L. & Fisher, M. P. A. Transport in a one-channel Luttinger liquid. Phys. Rev. Lett. 68, 1220–1223 (1992).
Chang, A. M. Chiral Luttinger liquids at the fractional quantum Hall edge. Rev. Mod. Phys. 75, 1449–1505 (2003).
Steinberg, H. et al. Charge fractionalization in quantum wires. Nature Phys. 4, 116–119 (2008).
Ashoori, R. C., Stormer, H. L., Pfeiffer, L. N., Baldwin, K. W. & West, K. Edge magnetoplasmons in the time domain. Phys. Rev. B 45, 3894–3897 (1992).
Fetter, A. L. Edge magnetoplasmons in a bounded two-dimensional electron fluid. Phys. Rev B 32, 7676–7684 (1985).
Volkov, V. A. & Mikhailov, S. A. Edge magnetoplasmons: low frequency weakly damped excitations in inhomogeneous two-dimensional electron systems. Sov. Phys. JETP 67, 1639–1653 (1988).
Talyanskii, V. I. et al. Spectroscopy of a two-dimensional electron gas in the quantum-Hall-effect regime by use of low-frequency edge magnetoplasmons. Phys. Rev. B 46, 12427–12432 (1992).
Hashisaka, M. et al. Distributed-element circuit model of edge magnetoplasmon transport. Phys. Rev. B 88, 235409 (2013).
Chklovskii, D. B., Shklovskii, B. I. & Glazman, L. I. Electrostatics of edge channels. Phys. Rev. B 46, 4026–4034 (1992).
Kumada, N., Kamata, H. & Fujisawa, T. Edge magnetoplasmon transport in gated and ungated quantum Hall systems. Phys. Rev. B 84, 045314 (2011).
Lee, H. C. & Yang, S.-R. E. Spin-charge separation in quantum Hall edge liquids. Phys. Rev. B 56, R15529–R15532 (1997).
Bocquillon, E. et al. Separation of neutral and charge modes in one-dimensional chiral edge channels. Nature Commun. 4, 1839 (2013).
Roulleau, P. et al. Direct measurement of the coherence length of edge states in the integer quantum Hall regime. Phys. Rev. Lett. 100, 126802 (2008).
Gabelli, J. et al. Relaxation time of a chiral quantum R–L circuit. Phys. Rev. Lett. 98, 166806 (2007).
Larkin, I. A. & Davies, J. H. Edge of the two-dimensional electron gas in a gated heterostructure. Phys. Rev. B 52, R5535–R5538 (1995).
Acknowledgements
The authors thank K-I. Imura and M. Nakamura for discussions and M. Ueki for experimental support. This work was partially supported by Grants-in-Aid for Scientific Research (21000004, 11J09248) and the Global Center of Excellence Program from the MEXT of Japan through the ‘Nanoscience and Quantum Physics’ Project of the Tokyo Institute of Technology.
Author information
Authors and Affiliations
Contributions
H.K. performed the experiments, analysed the data and wrote the manuscript. T.F. supervised the research. K.M. grew the wafer. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary Information (PDF 868 kb)
Rights and permissions
About this article
Cite this article
Kamata, H., Kumada, N., Hashisaka, M. et al. Fractionalized wave packets from an artificial Tomonaga–Luttinger liquid. Nature Nanotech 9, 177–181 (2014). https://doi.org/10.1038/nnano.2013.312
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nnano.2013.312
This article is cited by
-
Non-thermal Tomonaga-Luttinger liquid eventually emerging from hot electrons in the quantum Hall regime
Communications Physics (2023)
-
Quantized charge fractionalization at quantum Hall Y junctions in the disorder dominated regime
Nature Communications (2021)
-
Intriguing one-dimensional electronic behavior in emerging two-dimensional materials
Nano Research (2021)
-
Unveiling the bosonic nature of an ultrashort few-electron pulse
Nature Communications (2018)
-
Waveform measurement of charge- and spin-density wavepackets in a chiral Tomonaga–Luttinger liquid
Nature Physics (2017)