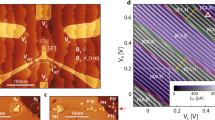
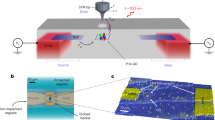
Abstract
The ability to control matter at the atomic scale and build devices with atomic precision is central to nanotechnology. The scanning tunnelling microscope1 can manipulate individual atoms2 and molecules on surfaces, but the manipulation of silicon to make atomic-scale logic circuits has been hampered by the covalent nature of its bonds. Resist-based strategies have allowed the formation of atomic-scale structures on silicon surfaces3, but the fabrication of working devices—such as transistors with extremely short gate lengths4, spin-based quantum computers5,6,7,8 and solitary dopant optoelectronic devices9—requires the ability to position individual atoms in a silicon crystal with atomic precision. Here, we use a combination of scanning tunnelling microscopy and hydrogen-resist lithography to demonstrate a single-atom transistor in which an individual phosphorus dopant atom has been deterministically placed within an epitaxial silicon device architecture with a spatial accuracy of one lattice site. The transistor operates at liquid helium temperatures, and millikelvin electron transport measurements confirm the presence of discrete quantum levels in the energy spectrum of the phosphorus atom. We find a charging energy that is close to the bulk value, previously only observed by optical spectroscopy10.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Binnig, G., Rohrer, H., Gerber, C. & Weibel, E. Tunneling through a controllable vacuum gap. Appl. Phys. Lett. 40, 178–180 (1982).
Eigler, D. M. & Schweizer, E. K. Positioning single atoms with a scanning tunnelling microscope. Nature 344, 524–526 (1990).
Lopinski, G. P., Wayner, D. D. M. & Wolkow, R. A. Self-directed growth of molecular nanostructures on silicon. Nature 406, 48–51 (2000).
Frank, D. J. et al. Device scaling limits of Si MOSFETs and their application dependencies. Proc. IEEE 89, 259–288 (2001).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Vrijen, R. et al. Electron-spin-resonance transistors for quantum computing in silicon–germanium heterostructures. Phys. Rev. A 62, 012306 (2000).
Hollenberg, L. C. L., Greentree, A. D., Fowler, A. G. & Wellard, C. J. Two dimensional architectures for donor based quantum computing. Phys. Rev. B 74, 045311 (2006).
Morton, J. J. L., McCamey, D. R., Eriksson, M. A. & Lyon, S. A. Embracing the quantum limit in silicon computing. Nature 479, 345–353 (2011).
Koenraad, P. M. & Flatté, M. E. Single dopants in semiconductors. Nature Mater. 10, 91–100 (2011).
Ramdas, A. K. & Rodriguez, S. Spectroscopy of the solid-state analogs of the hydrogen atom: donors and acceptors in semiconductors. Rep. Prog. Phys. 44, 1297–1387 (1981).
Roy, S. & Asenov, A. Where do the dopants go? Science 309, 388–390 (2005).
Shinada, T., Okamoto, S., Kobayashi, T. & Ohdomari, I. Enhancing semiconductor device performance using ordered dopant arrays. Nature 437, 1128–1131 (2005).
Zhirnov, V. V., Cavin, R. K., Hutchby, J. A. & Bourianoff, G. I. Limits to binary logic switch scaling—a Gedanken model. Proc. IEEE 91, 1934–1939 (2003).
Lansbergen, G. P. et al. Gate-induced quantum-confinement transition of a single dopant atom in a silicon FinFET. Nature Phys. 4, 656–661 (2008).
Calvet, L. E., Snyder, J. P. & Wernsdorfer, W. Excited-state spectroscopy of single Pt atoms in Si. Phys. Rev. B 78, 195309 (2008).
Tan, K. Y. et al. Transport spectroscopy of single phosphorus donors in a silicon nanoscale transistor. Nano Lett. 10, 11–15 (2010).
Pierre, M. et al. Single-donor ionization energies in a nanoscale CMOS channel. Nature Nanotech. 5, 133–137 (2010).
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nature Mater. 11, 143–147 (2012).
Morello, A. et al. Single-shot readout of an electron spin in silicon. Nature 467, 687–691 (2010).
Hollenberg, L. C. L. et al. Charge-based quantum computing using single donors in semiconductors. Phys. Rev. B 69, 113301 (2004).
Koiller, B., Hu, X. D. & Das Sarma, S . Exchange in silicon-based quantum computer architecture. Phys. Rev. Lett. 88, 027903 (2002).
Lyding, J. W., Shen, T. C., Hubacek, J. S., Tucker, J. R. & Abeln, G. C. Nanoscale patterning and oxidation of H-passivated Si(100)-2×1 surfaces with an ultrahigh-vacuum scanning tunneling microscope. Appl. Phys. Lett. 64, 2010–2012 (1994).
Schofield, S. R. et al. Atomically precise placement of single dopants in Si. Phys. Rev. Lett. 91, 136104 (2003).
Fuhrer, A., Füchsle, M., Reusch, T. C. G., Weber, B. & Simmons, M. Y. Atomic-scale, all epitaxial in-plane gated donor quantum dot in silicon. Nano Lett. 9, 707–710 (2009).
Wilson, H. F. et al. Thermal dissociation and desorption of PH3 on Si(001): a reinterpretation of spectroscopic data. Phys. Rev. B 74, 195310 (2006).
Klimeck, G., Lake, R., Bowen, R. C., Frensley, W. R. & Moise, T. S. Quantum device simulation with a generalized tunneling formula. Appl. Phys. Lett. 67, 2539–2541 (1995).
Rahman, R. et al. Electric field reduced charging energies and two-electron bound excited states of single donors in silicon. Phys. Rev. B 84, 115428 (2011).
Klimeck, G., Oyafuso, F., Boykin, T. B., Bowen, R. C. & von Allmen, P. Development of a nanoelectronic 3D (NEMO 3D) simulator for multimillion atom simulations and its application to alloyed quantum dots. Comput. Model. Eng. Sci. 3, 601–642 (2002).
Lee, S. et al. Electronic structure of realistically extended, atomistically resolved disordered Si:P δ-doped layers. Phys. Rev. B 84, 205309 (2011).
Weber, B. et al. Ohm's law survives to the atomic scale. Science 335, 64–67 (2012).
Acknowledgements
The authors acknowledge discussions with S. Rogge, J. Verduijn and R. Rahman. This research was conducted by the Australian Research Council Centre of Excellence for Quantum Computation and Communication Technology (project no. CE110001027). The research was also supported by the US National Security Agency and the US Army Research Office (contract no. W911NF-08-1-0527). M.Y.S. acknowledges a Federation Fellowship. L.H. acknowledges an Australian Professorial Fellowship.
Author information
Authors and Affiliations
Contributions
M.F. and J.M. carried out the fabrication and measurements. M.F., J.M., S.M., O.W., M.S., G.K. and L.H. analysed the data. H.R. and S.L. carried out the calculations. M.S. planned the project. G.K. and L.H. planned the modelling approach. M.F., J.M., S.M., H.R., G.K., L.H. and M.S. prepared the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Fuechsle, M., Miwa, J., Mahapatra, S. et al. A single-atom transistor. Nature Nanotech 7, 242–246 (2012). https://doi.org/10.1038/nnano.2012.21
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nnano.2012.21
This article is cited by
-
EUV-induced hydrogen desorption as a step towards large-scale silicon quantum device patterning
Nature Communications (2024)
-
Atomic-scale manipulation of buried graphene–silicon carbide interface by local electric field
Communications Physics (2024)
-
A solid-state quantum microscope for wavefunction control of an atom-based quantum dot device in silicon
Nature Electronics (2023)
-
Qubit-controlled directional edge states in waveguide QED
npj Quantum Information (2023)
-
Uncovering anisotropic effects of electric high-moment dipoles on the tunneling current in \(\delta\)-layer tunnel junctions
Scientific Reports (2023)