Abstract
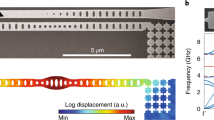
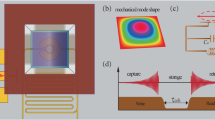
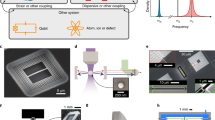
The ability to control mechanical motion with optical forces has made it possible to cool mechanical resonators to their quantum ground states. The same techniques can also be used to amplify rather than reduce the mechanical motion of such systems. Here, we study nanomechanical resonators that are slightly buckled and therefore have two stable configurations, denoted ‘buckled up’ and ‘buckled down’, when they are at rest. The motion of these resonators can be described by a double-well potential with a large central energy barrier between the two stable configurations. We demonstrate the high-amplitude operation of a buckled resonator coupled to an optical cavity by using a highly efficient process to generate enough phonons in the resonator to overcome the energy barrier in the double-well potential. This allows us to observe the first evidence for nanomechanical slow-down and a zero-frequency singularity predicted by theorists. We also demonstrate a non-volatile mechanical memory element in which bits are written and reset by using optomechanical backaction to direct the relaxation of a resonator in the high-amplitude regime to a specific stable configuration.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Marquardt, F. & Girvin, S. M. Optomechanics. Physics 2, 40 (2009).
Kippenberg, T. J. & Vahala, K. J. Cavity optomechanics: back-action at the mesoscale. Science 321, 1172–1176 (2008).
Schliesser, A., Arcizet, O., Riviere, R., Anetsberger, G. & Kippenberg, T. J. Resolved-sideband cooling and position measurement of a micromechanical oscillator close to the Heisenberg uncertainty limit. Nature Phys. 5, 509–514 (2009).
Riviere, R. et al. Optomechanical sideband cooling of a micromechanical oscillator close to the quantum ground state. Phys. Rev. A 83, 063835 (2011).
Gröblacher, S. et al. Demonstration of an ultracold micro-optomechanical oscillator in a cryogenic cavity. Nature Phys. 5, 485–488 (2009).
Naik, A. et al. Quantum measurement backaction and cooling observed with a nanomechanical resonator. Nature 443, 193–196 (2006).
Poot, M. & van der Zant, H. S. J. Mechanical systems in the quantum regime. Preprint at http://arxiv.org/abs/1106.2060v1 (2011).
Teufel, J. D. et al. Sideband cooling micromechanical motion to the quantum ground state. Nature 475, 359–363 (2011).
Chan, J. et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478, 89–92 (2011).
O'Connell, A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697–703 (2010).
Braginsky, V. B., Strigin, S. E. & Vyatchanin, S. P. Parametric oscillatory instability instability in Fabry–Perot interferometer. Phys. Lett. A. 287, 331–338 (2001).
Arcizet, O., Cohadon, P.-F., Briant, T., Pinard, M. & Heidmann, A. Radiation-pressure cooling and optomechanical instability of a micromirror. Nature 444, 71–74 (2006).
Mamin, H. J. & Rugar, D. Sub-attonewton force detection at millikelvin temperatures. Appl. Phys. Lett. 79, 3358–3360 (2001).
Liftshitz, R. & Cross, M. C. in Nonlinear Dynamics (eds Radons, G., Rumpf, B. & Schuster, H. G.) (Wiley-VCH, 2010).
Savel'ev, S., Hu, X. D. & Nori, F. Quantum electrodynamics: qubits from buckling nanobars. New J. Phys. 8, 105 (2006).
Rabl, P. et al. A quantum spin transducer based on nanoelectromechanical resonator arrays. Nature Phys. 6, 602–608 (2010).
Nguyen, C. T. C. Frequency-selective MEMs for miniaturized low-power communication devices. IEEE Trans. Microw. Theory Tech. 47, 1486–1503 (1999).
Yang, Y. T., Callegari, C., Feng, X. L., Ekinci, K. L. & Roukes, M. L. Zeptogram-scale nanomechanical mass sensing. Nano Lett. 6, 583–586 (2006).
Liu, N. et al. Time-domain control of ultrahigh-frequency nanomechanical systems. Nature Nanotech. 3, 715–719 (2008).
Hossein-Zadeh, M. & Vahala, K. J. Observation of injection locking in an optomechanical RF oscillator. Appl. Phys. Lett. 93, 191115 (2008).
Henrich, G., Ludwig, M., Qiang, J., Kubala, B. & Marquardt, F. Collective dynamics in optomechanical arrays. Preprint at http://arxiv.org/abs/1007.4819 (2010).
Wiederhecker, G. S., Chen, L., Gondarenko, A. & Lipson, M. Controlling photonic structures using optical forces. Nature 462, 633–636 (2009).
Rosenberg, J., Lin, Q. & Painter, O. Static and dynamic wavelength routing via the gradient optical force. Nature Photon. 3, 478–483 (2009).
Postma, H. W. C., Kozinsky, I., Husain, A. & Roukes, M. L. Dynamic range of nanotube- and nanowire-based electromechanical systems. Appl. Phys. Lett. 86, 223105 (2005).
Dorsel, A., McCullen, J. D., Meystre, P., Vignes, E. & Walther, H. Optical bistability and mirror confinement induced by radiation pressure. Phys. Rev. Lett. 51, 1550–1553 (1983).
Sheard, B. S., Gray, M. B., Mow-Lowry, C. M. & McClelland, D. E. Observation and characterization of an optical spring. Phys. Rev A 69, 051801 (2004).
Weis, S. et al. Optomechanically induced transparency. Science 330, 1520–1523 (2010).
Safavi-Naeini, A. H. et al. Electromagnetically induced transparency and slow light with optomechanics. Nature 472, 69–73 (2011).
Teufel, J. D. et al. Circuit cavity electromechanics in the strong-coupling regime. Nature 471, 204–208 (2011).
Dykman, A. et al. Spectral density of fluctuations of a double-well Duffing oscillator driven by white noise. Phys. Rev. A 37, 1303–1313 (1988).
Halg, B. On a micro-electro-mechanical nonvolatile memory Cell. IEEE Trans. Electron. Device 37, 2230–2236 (1990).
Rueckes, T. et al. Carbon nanotube-based nonvolatile random access memory for molecular computing. Science 289, 94–97 (2000).
Roodenburg, D., Spronck, J. W., Van der Zant, H. S. J. & Venstra, W. J. Buckling beam micromechanical memory with on-chip readout. Appl. Phys. Lett. 94, 123108 (2009).
Mahboob, I. & Yamaguchi, H. Bit storage and bit flip operations in an electromechanical oscillator. Nature Nanotech. 3, 275–279 (2008).
Venstra, W. J., Westra, H. J. R., & Van der Zant, H. S. J. Mechanical stiffening, bistability, and bit operations in a microcantilever. Appl. Phys. Lett. 97, 193107 (2010).
Freeman, M. & Heibert, W. Taking another swing at computing. Nature Nanotech. 3, 251–252 (2008).
Jang, J. E. et al. Nanoscale memory cell based on nanoelectromechanical switched capacitor. Nature Nanotech. 3, 26–30 (2008).
Li, M. et al. Harnessing optical forces in integrated photonic circuits. Nature 456, 480–484 (2008).
Krylov, S., Ilic, B. R., Schreiber, D., Seretensky, S. & Craighead, H. The pull-in behavior of electrostatically actuated bistable microstructures. J. Micromech. Microeng. 18, 055026 (2008).
Feng, X. L., White, C. J., Hajimiri, A. & Roukes, M. L. A self-sustaining ultrahigh-frequency nanoelectromechanical oscillator. Nature Nanotech. 3, 342–346 (2008).
Kippenberg, T. J., Rokhsari, H., Carmon, T., Scherer, A. & Vahala, K. J. Analysis of radiation-pressure induced mechanical oscillation of an optical microcavity. Phys. Rev. Lett. 95, 033901 (2005).
Marquardt, F., Harris, J. G. E. & Girvin, S. M. Dynamical multistability induced by radiation pressure in high-finesse micromechanical optical cavities. Phys Rev. Lett. 96, 103901 (2006).
Metzger, C. et al. Self-induced oscillations in an optomechanical system driven by bolometric backaction. Phys Rev. Lett. 101, 133903 (2008).
Anetsberger, G. et al. Near-field cavity optomechanics with nanomechanical oscillators. Nature Phys. 5, 909–914 (2009).
Voigtlaender, K. & Risken H. Solutions of the Fokker–Planck equation for a double-well potential in terms of matrix continued fractions. J. Stat. Phys. 40, 397–429 (1985).
Soskin, S. M., Mannella, R. & McClintock, P. V. E. Zero-dispersion phenomena in oscillatory systems. Phys. Rep. 73, 247–408 (2003).
Cross, M. C., Zumdieck, A., Lifshitz, R. & Rogers, J. L. Synchronization by nonlinear frequency pulling. Phys. Rev. Lett. 93, 224101 (2004).
Badzey, R. L., Zolfagharkhani, G., Gaidarzhy, A. & Mohanty, P. A controllable nanomechanical memory element. Appl. Phys. Lett. 85, 3587–3589 (2004).
Acknowledgements
The authors thank M. Rooks (Yale Institute for Nanoscience and Quantum Engineering) for help with electron-beam lithography, and M. Power for help with device fabrication. The authors also acknowledge funding support from the DARPA/MTO ORCHID programme through a grant from the Air Force Office of Scientific Research (AFOSR). H.X.T. acknowledges support from a Packard Fellowship in Science and Engineering and a career award from the National Science Foundation. M.P. acknowledges a Rubicon fellowship from the Netherlands Organization for Scientific Research (NWO)/Marie Curie Cofund Action.
Author information
Authors and Affiliations
Contributions
M.B. performed the device fabrication and carried out measurements and data analysis under the supervision of H.X.T. M.B. and M.P. contributed to numerical analysis of the coupled optomechanical system. M.B., M.P., M.L., W.P.H.P. and H.X.T. discussed the results and all authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1152 kb)
Rights and permissions
About this article
Cite this article
Bagheri, M., Poot, M., Li, M. et al. Dynamic manipulation of nanomechanical resonators in the high-amplitude regime and non-volatile mechanical memory operation. Nature Nanotech 6, 726–732 (2011). https://doi.org/10.1038/nnano.2011.180
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nnano.2011.180
This article is cited by
-
Microcavity phonoritons – a coherent optical-to-microwave interface
Nature Communications (2023)
-
Controllable branching of robust response patterns in nonlinear mechanical resonators
Nature Communications (2023)
-
Nonlinear interactions between vibration modes with vastly different eigenfrequencies
Communications Physics (2023)
-
Integrated optical memristors
Nature Photonics (2023)
-
Sliding nanomechanical resonators
Nature Communications (2022)