Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Weighted combination of size and disparity: a computational model for timing a ball catch

Nature Neuroscience volume 2, pages 186–190 (1999)Cite this article

Abstract

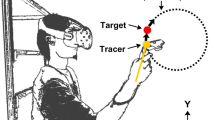
How do we time hand closure to catch a ball? Binocular disparity and optical looming provide two sources of information about an object's motion in depth, but the relative effectiveness of the two cues depends on ball size. Based on results from a virtual reality ball–catching task, we derive a simple model that uses both cues. The model is sensitive to the relative effectiveness of size and disparity and implicitly switches its response to the cue that specifies the earliest arrival and away from a cue that is lost or below threshold. We demonstrate the model's robustness by predicting the response of participants to some very unusual ball trajectories in a virtual reality task.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Retinotopic and spatiotopic information for TTC judgment.
Figure 2: Changes in the timing of hand grasp when catching virtual balls.
Figure 3: Predictions from the dipole model and a modular model for the plateau conditions of Experiment 2.
Figure 4: Errors in grasp timing for the ball–catching task in Experiment 2.

Similar content being viewed by others

References

  1. Sun, H. & Frost, B. J. Computation of different optical variables of looming objects in pigeon nucleus rotundus neurons. Nat. Neurosci. 4, 296–303 (1998).

    Article  Google Scholar 

  2. Regan, D. & Beverley, K. I. Binocular and monocular stimuli for motion in depth: Changing–disparity and changing–size feed the same motion in depth stage. Vision Res. 19, 1331–1342 (1979).

    Article  CAS  Google Scholar 

  3. Lee, D. N. A theory of visual control of braking based on information about time–to–collision. Perception 5, 437–459 (1976).

    Article  CAS  Google Scholar 

  4. Regan, D. & Hamstra, S. J. Dissociation of discrimination thresholds for time to contact and for rate of angular expansion. Vision Res. 33, 447–462 (1993).

    Article  CAS  Google Scholar 

  5. Heuer, H. Estimates of time to contact based on changing size and changing target vergence. Perception 22, 549–563 (1993).

    Article  CAS  Google Scholar 

  6. Gray, R. & Regan, D. Accuracy of estimating time to collision using binocular and monocular information. Vision Res. 38, 499–512 (1997).

    Article  Google Scholar 

  7. Wann, J. P. Anticipating arrival: is the tau–margin a specious theory? J. Exp Psychol. Hum. Percept. Perform. 22, 1031– 1048 (1996).

    Article  CAS  Google Scholar 

  8. Tresilian, J. R. Perceptual and motor processes in interceptive timing. Hum. Mov. Sci 13, 335–373 ( 1994).

    Article  Google Scholar 

  9. Laurent, M., Montagne, G. & Durey, A. Binocular invariants in interception tasks: a directed perception approach. Perception 25, 1437 –1450 (1996).

    Article  Google Scholar 

  10. Regan, D., Erkelens C. J. & Collewijn, H. Necessary conditions for the perception of motion in depth. Invest. Ophthalmol. Vision Sci. 27, 584–597 (1986).

    CAS  Google Scholar 

  11. Milner, A. D. & Goodale, M. A. The Visual Brain in Action (Oxford Univ. Press, Oxford, 1996).

    Google Scholar 

  12. Alderson, G. J. K., Sully, D. J. & Sully, H. G. An operational analysis of a one–handed catching task using high–speed photography. J. Motor Behav. 6, 217–226 (1974).

    Article  CAS  Google Scholar 

  13. Tresilian, J. R. Perceptual and cognitive processes in time–to–contact estimation: Analysis of prediction–motion and relative judgment tasks. Percept. Psychophys. 57, 231–245 (1995).

    Article  CAS  Google Scholar 

  14. Landy, M. S., Maloney, L. T., Johnston, E. B. & Young, M. J. Measurement and modeling of depth cue combination: In defense of weak fusion. Vision Res. 35, 389–412 (1995).

    Article  CAS  Google Scholar 

  15. Dobbins, A. C., Jeo, R. M., Fiser, J. & Allman, J. M. Distance modulation of neural activity in visual cortex. Science 281, 552–555 (1998).

    Article  CAS  Google Scholar 

  16. Julesz, B. Textons, the elements of texture perception and their interactions. Nature 290, 91–97 ( 1981).

    Article  CAS  Google Scholar 

  17. Regan, D. Visual judgements and misjudgements in cricket, and the art of flight. Perception 21, 91–115 ( 1992).

    Article  CAS  Google Scholar 

  18. Peper, C. L., Bootsma, R. J., Mestre, D. R. & Bakker, F. C. Catching balls: How to get the hand to the right place at the right time. J. Exp Psychol. Hum. Percept. Perform. 20, 591–612 (1994).

    Article  CAS  Google Scholar 

Download references

Acknowledgements

We thank Anna Plooy and Martin Smyth for their input to the second experiment and also Julie Harris, Mike Harris and Graham Schafer for incisive comments. This research was supported by the UK EPSRC GR/L18693 and GR/L16125.

Author information

Authors and Affiliations

  1. Department of Psychology, University of Edinburgh, 7 George Square, Edinburgh, EH8 9JZ, UK

    Simon K. Rushton

  2. Department of Psychology, University of Reading, 3 Earley Gate, Reading, RG6 6AL, UK

    John P. Wann

Authors
  1. Simon K. Rushton
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. John P. Wann
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to John P. Wann.

Supplementary information

Supplementary Information

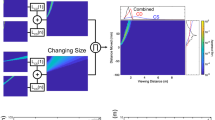
Three models that combine binocular and monocular information to estimate time to contact (TTC). (a) Fixed weighting of optic size and disparity. TTC is estimated from each input and then averaged on the basis of some weighting (0 <β < 1). This approach, however, is not robust if one input is perturbed or lost, and so it will produce large errors of estimation. (b) Variable weighting of optic size and disparity. Each modular estimate is first summated (Σ) and then a cross ratio from the opposing input is used to calculate the β weightings (see Results). (c) The dipole model. Binocular and monocular motion is combined before estimating TTC. If one of the inputs is perturbed or drops out, this approach has the advantages of model (b) without the explicit iterative calculation of β weights in flight. Note that in all three models the recovery of the binocular angular subtense φ would be required for a veridical estimate of TTC from disparity, but for many natural environments relative disparity α is approximately equal to φ (see Mathematical Appendix). (GIF 26 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rushton, S., Wann, J. Weighted combination of size and disparity: a computational model for timing a ball catch. Nat Neurosci 2, 186–190 (1999). https://doi.org/10.1038/5750

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1038/5750

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing