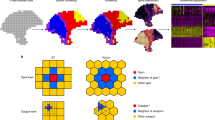
Abstract
Technological advances have made it possible to measure spatially resolved gene expression at high throughput. However, methods to analyze these data are not established. Here we describe SpatialDE, a statistical test to identify genes with spatial patterns of expression variation from multiplexed imaging or spatial RNA-sequencing data. SpatialDE also implements 'automatic expression histology', a spatial gene-clustering approach that enables expression-based tissue histology.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
Accession codes
References
Lee, J.H. Wiley Interdiscip. Rev. Syst. Biol. Med. 9, e1369 (2017).
Achim, K. et al. Nat. Biotechnol. 33, 503–509 (2015).
Satija, R., Farrell, J.A., Gennert, D., Schier, A.F. & Regev, A. Nat. Biotechnol. 33, 495–502 (2015).
Junker, J.P. et al. Cell 159, 662–675 (2014).
Chen, J. et al. Nat. Protoc. 12, 566–580 (2017).
Ståhl, P.L. et al. Science 353, 78–82 (2016).
Shah, S., Lubeck, E., Zhou, W. & Cai, L. Neuron 92, 342–357 (2016).
Moffitt, J.R. et al. Proc. Natl. Acad. Sci. USA 113, 11046–11051 (2016).
Brennecke, P. et al. Nat. Methods 10, 1093–1095 (2013).
Pettit, J.-B. et al. PLOS Comput. Biol. 10, e1003824 (2014).
Lippert, C. et al. Nat. Methods 8, 833–835 (2011).
Takamori, S., Rhee, J.S., Rosenmund, C. & Jahn, R. Nature 407, 189–194 (2000).
Seewaldt, V.L. Nature 490, 490–491 (2012).
Reimand, J. et al. Nucleic Acids Res. 44, W83–W89 (2016).
Andrews, T.S. & Hemberg, M. bioRxiv Preprint at https://www.biorxiv.org/content/early/2016/10/20/065094 (2016).
Chen, K.H., Boettiger, A.N., Moffitt, J.R., Wang, S. & Zhuang, X. Science 348, aaa6090 (2015).
Battich, N., Stoeger, T. & Pelkmans, L. Cell 163, 1596–1610 (2015).
Owens, N.D.L. et al. Cell Rep. 14, 632–647 (2016).
Kalaitzis, A.A. & Lawrence, N.D. BMC Bioinformatics 12, 180 (2011).
Durrande, N., Hensman, J., Rattray, M. & Lawrence, N.D. PeerJ Comput. Sci. 2, e50 (2016).
Rasmussen, C.E. & Williams, C.K.I. Gaussian Processes for Machine Learning (MIT Press, 2006).
Zhou, X. & Stephens, M. Nat. Genet. 44, 821–824 (2012).
Storey, J.D. & Tibshirani, R. Proc. Natl. Acad. Sci. USA 100, 9440–9445 (2003).
Bishop, C.M. Pattern Recognition and Machine Learning (Springer, 2006).
Wolf, F.A., Angerer, P. & Theis, F.J. Genome Biol. 19, 15 (2018).
Krige, D.G. J. S. Afr. Inst. Min. Metall. 52, 119–139 (1951).
Stegle, O. et al. J. Comput. Biol. 17, 355–367 (2010).
Lönnberg, T. et al. Sci. Immunol. 2, eaal2192 (2017).
Äijö, T. et al. Bioinformatics 30, i113–i120 (2014).
Macaulay, I.C. et al. Cell Rep. 14, 966–977 (2016).
Eckersley-Maslin, M.A. et al. Cell Rep. 17, 179–192 (2016).
Lloyd, J.R., Duvenaud, D., Grosse, R., Tenenbaum, J.B. & Ghahramani, Z. in Proceedings of the Twenty-eighth AAAI Conference on Artificial Intelligence 1242–1250 (AAAI Press, 2014).
Acknowledgements
The authors thank D. Arnol and F.P. Casale for helpful advice on statistics and data normalization. J. Moffitt helped us understand the data format for available MERFISH data. In addition, we thank A. Lun, M. Hemberg, D. Kunz, and K. Meyer for feedback on the manuscript. This work was supported by the EMBL (EMBL International PhD Program support to V.S.; core funding to O.S.), the Wellcome Trust (S.A.T. and O.S.), the ERC (Consolidator Grant “ThDEFINE” to S.A.T.), and the EU (O.S.).
Author information
Authors and Affiliations
Contributions
V.S. and O.S. conceived the method. V.S. implemented the method and generated the results. V.S., S.A.T., and O.S. interpreted the results and wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Integrated supplementary information
Supplementary Figure 1 Model selection of different covariance functions.
In addition to the hypothesis test of spatial vs non-spatial expression variance, SpatialDE can be used to classify spatially variable genes into genes with periodic, linear patterns, or general spatial patterns. Illustrative examples of simulated functional dependencies are shown below the corresponding covariance matrices.
Supplementary Figure 2 Computational efficiency of SpatialDE.
Compared is the SpatialDE native implementation versus a Stan implementation of the same model. Caching operations and linear algebra speedups are used where possible, enabling tractable genome-wide analyses with thousands of samples or cells. Shown is the empirical runtime for the SpatialDE test applied to 10,000 genes, using a late 2013 iMac with 3.2 GHz Intel Core i5 processor.
Supplementary Figure 3 Expanded example of spatially variable genes identified in the mouse olfactory bulb data.
Spatial expression patterns for 25 additional SV genes (out of 67, FDR<0.05, Q-value adjusted), selected to represent expression patterns with different function periods and length scales.
Supplementary Figure 4 Results from automatic expression histology.
(A) AEH applied to spatial transcriptomics data of mouse olfactory bulb, for K=5 spatial expression patterns. Color denotes the expression level of the inferred spatial pattern. The number of genes assigned to each pattern is indicated in the title of each panel, with representative gene assignments listed below. (B) Same as A but considering AEH applied to spatial transcriptomics data from breast cancer biopsy. (C) As in A but for SeqFISH data from mouse hippocampus.
Supplementary Figure 5 Comparison to clustering analysis for the mouse olfactory bulb data.
(A) Principal component analysis using genome-wide expression profiles of individual “spots” for the mouse olfactory bulb data. The spots are color coded by the cluster assignment from conventional Bayesian Gaussian Mixture Modelling (K=4 clusters). (B) Bayesian Gaussian Mixture Model cluster assignment probabilities, discretizing the 260 spatial “spots” into four clusters (analysis ignores spatial structure). (C) Visualization of cluster membership in spatial context of the tissue. (D) Scatter plot of negative log P-values from an ANOVA test between clusters (x-axis) versus negative log P-values from the SpatialDE test. 52 genes were identified by both methods, while 15 genes were unique to SpatialDE. (E) Comparison of clusters of spots versus AEH patterns.
Supplementary Figure 6 SpatialDE applied to breast cancer biopsy tissue.
(A) Corresponding HE image of breast cancer tissue from spatial transcriptomics. (B) Fraction of variance explained by spatial variation (x-axis) versus SpatialDE negative log P-value (y-axis) for all genes. Dashed line corresponds to the FDR=0.05 significance threshold (N=115 genes, Q-value adjusted). Genes classified as periodically variable are shown in orange (N=22), genes with a general spatial dependency in blue (N=93). Disease-implicated genes annotated based on prior knowledge (Stahl et al.6) are highlighted with red labels. Other representative genes are annotated with black labels. The X symbol shows the result of applying SpatialDE to the estimated total RNA content per spot. (C) Visualization of 37 selected spatially variable genes with different periods and length scales. The black scale bar corresponds to 1 mm. Colors and labels as in (Fig. 2). Stars next to gene names denote significance levels (* FDR < 0.05, ** FDR < 0.01, *** FDR < 0.001, Q-value adjusted) of spatial variation.
Supplementary Figure 7 Comparison to differential expression analysis using unsupervised clustering of spots.
(A) Principal component analysis using genome-wide expression profiles of individual “spots” from the spatial transcriptomics breast cancer data, color coded by cluster membership for K=4 clusters (using Bayesian Gaussian Mixture Modelling). (B) Bayesian Gaussian Mixture Model cluster probabilities, discretizing the 250 spatial breast cancer “spots” into four clusters (analysis ignores spatial structure). (C) Visualization of cluster membership in the original tissue context. (D) Scatter plot of negative log P-values from an ANOVA test between clusters (x-axis) versus negative log P-values of spatial variation from SpatialDE (y-axis). 83 genes were identified as significantly variable by both approaches (FDR<0.05, Q-value adjusted); 32 genes are significant only in the SpatialDE test, among them immune genes. (E) Histogram of the fitted length scales for SV genes detected by both approaches (blue) and SV genes exclusively detected by SpatialDE (orange). Genes that were only detected by SpatialDE were associated with smaller length scales, indicating localized expression patterns.
Supplementary Figure 8 Comparison of SpatialDE to alternative measures of expression heterogeneity in the breast cancer tissue.
(A) Comparison of adjusted negative log P-values from the SpatialDE test (y-axis) versus commonly used statistics for expression heterogeneity (x-axis) - Upper left: Mean, Upper right: Variance, Lower left: CV2 (squared coefficient of variation), Lower right: Dropout rate (fraction of cells/samples a gene is not detected in). Random selection of significant SV genes highlighted in red for context. No dependence between SpatialDE significance levels and expression level (mean) or variance was observed. Statistics calculated for 12,856 genes using 250 “spots”. (B) Comparison of significance of SV for genes identified by SpatialDE versus commonly used strategies for defining highly variable genes based on regression models between summary statistics: Relation with CV2 (Upper) or Variance (Middle), or with dropout fraction (Bottom). The rightmost column of plots show residuals compared with the SpatialDE significance; polynomial regression for CV2 and Variance, logistic regression for dropout rate. Significant SV genes as identified by SpatialDE (FDR<0.05, Q-value adjusted) are shown in grey. Other, non-significant genes are shown in solid black. The SV genes significance are orthogonal to HVG measures, indicating that spatial variation is different from general variability. Statistics calculated for 12,856 genes using 250 “spots”.
Supplementary Figure 9 Assessment of statistical calibration of SpatialDE through data randomization.
(A) QQ-plot of expected P-values (Chi2 distribution with 1 degree of freedom) versus observed P-values from the SpatialDE tests on the breast cancer data. (B) To simulate data from an empirical null, without spatial structure, expression values were shuffled among the sampled coordinates. Shown is the resulting expression pattern for COL3A1 expression, as representative example. (C) SpatialDE negative log P-values for genes on shuffled data, with the number of detected SV genes (FD<0.05) being consistent with the selected false discovery rate. (D) Analogous QQ-plot as in A on shuffled expression values. SpatialDE P-values follow the null distribution, indicating that the model is calibrated.
Supplementary Figure 10 Assessing statistical calibration of SpatialDE through simulations.
(A-B) Simulation of bell curve shaped data on the mouse olfactory bulb coordinates. (A) Example of six bell curves with different radii. (B) Results from applying SpatialDE to data from 3,000 bell curves with different radii and stratified over different levels of simulated noise (fraction of spatial variance, FSV). Red line denotes P=0.05 significance level, vertical blue dotted lines indicate smallest and largest pairwise distances observed in mouse olfactory bulb data respectively. Black dots denote negative log P-values (left axis), while blue dashes indicating statistical power for detecting true simulated SV genes (fraction true positives) for each bell radius (right axis). (C) Analogous results as in B, however when simulating data from the generative model underlying SpatialDE, considering different values for the fraction of spatial variance (FSV) and length scales, considering 3,000 simulations. (D) Scatter plot of inferred length scales (y-axis) versus simulated length scale (x-axis) for the data shown in C. (E) Simulation of 3,000 genes from the null model with no spatial covariance. Bars denote the fraction of (false positive) SV genes for different SpatialDE P-value thresholds (x-axis). The proportion of false positive genes was lower than the controlled family-wise error rate (FWER), indicating that the test is conservative.
Supplementary Figure 11 Expanded examples of spatially variable genes for the mouse hippocampus data set.
Visualization of 28 SV genes (out of 249, FDR<0.05, Q-value adjusted) from the mouse hippocampus SeqFISH data, displaying selected genes with periodic, linear, and general spatial dependencies with different estimated length scales. Black scale bar correspond to 50 μm. Colors and labels as in Fig. 2, stars next to gene names denote significance levels (* FDR < 0.05, ** FDR < 0.01, *** FDR < 0.001, Q-value adjusted).
Supplementary Figure 12 Visual inspection of genes from seqFISH data.
All 249 genes measured in the SeqFISH data. Plots are ordered left to right then top to down in order of decreasing significance of spatial variation using the SpatialDE test (in two columns, left column first). Stars next to gene names denote significance levels after correcting for multiple testing (* FDR < 0.05, ** FDR < 0.01, *** FDR < 0.001, Q-value adjusted).
Supplementary Figure 13 Application to MERFISH data.
(A) In a MERFISH study of an osteosarcoma cell culture of 139 probes from Moffitt et al, the SpatialDE test identified the majority of the probes as spatially variable (66%, FDR<0.05, dashed line, Q-value adjusted). 21 of 92 significant SV genes were assigned to a periodic function by the model, and nine genes had linear functions. Red labels indicate negative control probes. Genes indicated as enriched in proliferating cells in the original study are marked in green, and depleted genes in blue. (B) Visualization of the MERFISH data by plotting general RNA probes in pink and MALAT1 probes in blue on two 512 x 512 virtual pixel grids at different scales. The original imaged region was 5.2 mm wide and 8.2 mm high totaling 38,594 cells (upper). We analyzed a region of 1 mm x 1 mm in the middle of the cell culture with 1,056 cells (lower). (C) Expression levels in the cell culture region visualized for selected SV genes with various fitted periods and length scales (significance levels and colors as in Fig. 2). Black scale bar correspond to 200 μm. Stars next to gene names denote significance levels (* FDR < 0.05, ** FDR < 0.01, *** FDR < 0.001, Q-value adjusted). (D) Fraction of gene probes and control probes detected as significant SV genes as a function of the family-wise error rate (FWER). The number of significant control probes was in line with the FWER.
Supplementary Figure 14 Application to a gene expression time-course data set.
(A) SpatialDE applied to a developmental time course (89 time points from Owens et al), identifying the majority of genes as spatially variable (21,009 out of 22,256 genes, FDR < 0.05, Q-value adjusted). Of these, 241 were assigned to periodic patterns, and 269 were detected with linear trends. Colors and point sizes as in Fig. 2. The X marks indicates result of running SpatialDE on RNA spike-in content and the number of detected genes, proxies for the RNA content in the embryos. (B) Examples of temporally variable genes of various periods and length scales. Black scale bar corresponds to 12 hours in the time-course, periods and length scales of functions are indicated relative to this. Collection time in units of hours post fertilization (hpf). Stars next to gene names denote significance levels (* FDR < 0.05, ** FDR < 0.01, *** FDR < 0.001, Q-value adjusted). (C) The expression patterns of the top 400 significantly SV genes are visualized, ordered by the time they reach their highest expression value. Example genes from B are annotated.
Supplementary Figure 15 Subtle noise can affect spatial function classification.
(A) Nrgn which is assigned as periodic with posterior probability 1. Red line in top row indicates where in spatial coordinates the Gaussian processes are predicted in the bottom row, with a sliver of close by points colored in black. Bottom row shows expression level of all “spots”, with “spots” close to the predicted curves in black for spatial context. (B) Same as (A) but for Penk which have posterior probability 0.12 of being periodic. Noise at the right side of “Sliver 1” cause the periodic covariance to not fit the data as well as squared exponential covariance.
Supplementary information
Supplementary Text and Figures
Supplementary Figures 1–15 and Supplementary Note 1
Supplementary Table 1
Table with SpatialDE analysis results
Supplementary Software
SpatialDE Python package and usage examples, in addition to code and notebooks used to produce all results and figures.
Rights and permissions
About this article
Cite this article
Svensson, V., Teichmann, S. & Stegle, O. SpatialDE: identification of spatially variable genes. Nat Methods 15, 343–346 (2018). https://doi.org/10.1038/nmeth.4636
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmeth.4636
This article is cited by
-
spVC for the detection and interpretation of spatial gene expression variation
Genome Biology (2024)
-
Spatial multi-omics: novel tools to study the complexity of cardiovascular diseases
Genome Medicine (2024)
-
Evaluating spatially variable gene detection methods for spatial transcriptomics data
Genome Biology (2024)
-
SRT-Server: powering the analysis of spatial transcriptomic data
Genome Medicine (2024)
-
TISSUE: uncertainty-calibrated prediction of single-cell spatial transcriptomics improves downstream analyses
Nature Methods (2024)