Abstract
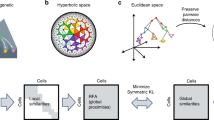
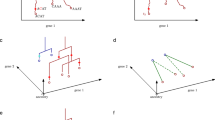
Single-cell trajectories can unveil how gene regulation governs cell fate decisions. However, learning the structure of complex trajectories with multiple branches remains a challenging computational problem. We present Monocle 2, an algorithm that uses reversed graph embedding to describe multiple fate decisions in a fully unsupervised manner. We applied Monocle 2 to two studies of blood development and found that mutations in the genes encoding key lineage transcription factors divert cells to alternative fates.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Trapnell, C. et al. Nat. Biotechnol. 32, 381–386 (2014).
Kumar, P., Tan, Y. & Cahan, P. Development 144, 17–32 (2017).
Setty, M. et al. Nat. Biotechnol. 34, 637–645 (2016).
Haghverdi, L., Büttner, M., Wolf, F.A., Buettner, F. & Theis, F.J. Nat. Methods 13, 845–848 (2016).
Mao, Q., Wang, L., Goodison, S. & Sun, Y. in Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 765–774 (ACM, 2015).
Mao, Q., Wang, L., Tsang, I. & Sun, Y. IEEE Trans. Pattern Anal. Mach. Intell. https://doi.org/10.1109/TPAMI.2016.2635657 (2016).
Rodriguez, A. & Laio, A. Science 344, 1492–1496 (2014).
Treutlein, B. et al. Nature 509, 371–375 (2014).
Olsson, A. et al. Nature 537, 698–702 (2016).
Paul, F. et al. Cell 163, 1663–1677 (2015).
Hastie, T. & Stuetzle, W. J. Am. Stat. Assoc. 84, 502–516 (1989).
Gorban, A.N. & Zinovyev, A.Y. in Handbook of Research on Machine-learning Applications and Trends: Algorithms, Methods, and Techniques 28–59 (Information Science Reference, Hershey, Pennsylvania, USA, 2009).
Bellman, R. The Theory of Dynamic Programming (DTIC Document, 1954).
Welch, J.D., Hartemink, A.J. & Prins, J.F. Genome Biol. 17, 106 (2016).
Qiu, X. et al. Nat. Methods 14, 309–314 (2017).
Qiu, X., Ding, S. & Shi, T. PLoS One 7, e49271 (2012).
Tang, Y., Yuan, R., Wang, G., Zhu, X. & Ao, P. arXiv:1611.07140 (2016).
Tirosh, I. et al. Nature 539, 309–313 (2016).
Cusanovich, D.A. et al. Science 348, 910–914 (2015).
Ramani, V. et al. Nat. Methods 14, 263–266 (2017).
Mao, Q., Yang, L., Wang, L., Goodison, S. & Sun, Y. . in Proceedings of the 2015 SIAM International Conference on Data Mining 792–800 (Society for Industrial and Applied Mathematics, 2015).
Boyd, S. & Vandenberghe, L. Convex Optimization (Cambridge University Press, Cambridge, 2004).
Rand, W.M. J. Am. Stat. Assoc. 66, 846–850 (1971).
Acknowledgements
We thank I. Tirosh for discussions on marker-based ordering, F. Theis and F.A. Wolf for discussions on the data analysis with DPT from Paul et al.9, and members of the Trapnell laboratory for comments on the manuscript. This work was supported by US National Institutes of Health (NIH) grants DP2 HD088158 (C.T.) and U54 DK107979 (C.T.); C.T. is partly supported by a Dale. F. Frey Award for Breakthrough Scientists and an Alfred P. Sloan Foundation Research Fellowship; and H.A.P. is supported by a National Science Foundation (NSF) Graduate Research Fellowship (DGE-1256082).
Author information
Authors and Affiliations
Contributions
X.Q., Q.M., and C.T. designed and implemented Monocle 2; X.Q. performed the analysis; Y.T. and L.W. contributed to the technical design; R.C. and H.A.P. performed the testing; C.T. conceived the project; and all authors wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Text and Figures
Supplementary Figures 1–20 and Supplementary Note. (PDF 20516 kb)
Life Sciences Reporting Summary
Life Sciences Reporting Summary. (PDF 129 kb)
Supplementary Data 1
Zipped file for the neuron simulation data. (ZIP 35169 kb)
Supplementary Data 2
Zipped file for the least action path data. (ZIP 401 kb)
Supplementary Data 3
Zipped file for the complicate tree structure data. (ZIP 3 kb)
Supplementary Software
Software and analysis code used in this study which can reproduce all results. (ZIP 15812 kb)
Rights and permissions
About this article
Cite this article
Qiu, X., Mao, Q., Tang, Y. et al. Reversed graph embedding resolves complex single-cell trajectories. Nat Methods 14, 979–982 (2017). https://doi.org/10.1038/nmeth.4402
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmeth.4402
This article is cited by
-
Single cell analysis reveals the roles and regulatory mechanisms of type-I interferons in Parkinson’s disease
Cell Communication and Signaling (2024)
-
An aging-related immune landscape in the hematopoietic immune system
Immunity & Ageing (2024)
-
Single-cell RNA sequencing reveals recruitment of the M2-like CCL8high macrophages in Lewis lung carcinoma-bearing mice following hypofractionated radiotherapy
Journal of Translational Medicine (2024)
-
SIRPB1 regulates inflammatory factor expression in the glioma microenvironment via SYK: functional and bioinformatics insights
Journal of Translational Medicine (2024)
-
The integration of single-cell and bulk RNA-seq atlas reveals ERS-mediated acinar cell damage in acute pancreatitis
Journal of Translational Medicine (2024)