Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Brief Communication
  • Published:

Efficient set tests for the genetic analysis of correlated traits

Nature Methods volume 12, pages 755–758 (2015)Cite this article

Subjects

Abstract

Set tests are a powerful approach for genome-wide association testing between groups of genetic variants and quantitative traits. We describe mtSet (http://github.com/PMBio/limix), a mixed-model approach that enables joint analysis across multiple correlated traits while accounting for population structure and relatedness. mtSet effectively combines the benefits of set tests with multi-trait modeling and is computationally efficient, enabling genetic analysis of large cohorts (up to 500,000 individuals) and multiple traits.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Assessment of scalability, calibration and power of mtSet.
Figure 2: Application of mtSet to six basal hematology traits in the rat data.

Similar content being viewed by others

References

  1. Kang, H.M. et al. Nat. Genet. 42, 348–354 (2010).

    Article  CAS  Google Scholar 

  2. Yang, J., Lee, S.H., Goddard, M.E. & Visscher, P.M. Am. J. Hum. Genet. 88, 76–82 (2011).

    Article  CAS  Google Scholar 

  3. Gusev, A. et al. Am. J. Hum. Genet. 95, 535–552 (2014).

    Article  CAS  Google Scholar 

  4. Wu, M.C. et al. Am. J. Hum. Genet. 86, 929–942 (2010).

    Article  CAS  Google Scholar 

  5. Quon, G., Lippert, C., Heckerman, D. & Listgarten, J. Nucleic Acids Res. 41, 2095–2104 (2013).

    Article  CAS  Google Scholar 

  6. Wu, M.C. et al. Am. J. Hum. Genet. 89, 82–93 (2011).

    Article  CAS  Google Scholar 

  7. Schifano, E.D. et al. Genet. Epidemiol. 36, 797–810 (2012).

    PubMed  PubMed Central  Google Scholar 

  8. Listgarten, J. et al. Bioinformatics 29, 1526–1533 (2013).

    Article  CAS  Google Scholar 

  9. Lippert, C. et al. Bioinformatics 30, 3206–3214 (2014).

    Article  CAS  Google Scholar 

  10. Solovieff, N., Cotsapas, C., Lee, P.H., Purcell, S.M. & Smoller, J.W. Nat. Rev. Genet. 14, 483–495 (2013).

    Article  CAS  Google Scholar 

  11. Aschard, H. et al. Am. J. Hum. Genet. 94, 662–676 (2014).

    Article  CAS  Google Scholar 

  12. Ferreira, M.A. & Purcell, S.M. Bioinformatics 25, 132–133 (2009).

    Article  CAS  Google Scholar 

  13. Bottolo, L. et al. PLoS Genet. 9, e1003657 (2013).

    Article  CAS  Google Scholar 

  14. Bolormaa, S. et al. PLoS Genet. 10, e1004198 (2014).

    Article  Google Scholar 

  15. Korte, A. et al. Nat. Genet. 44, 1066–1071 (2012).

    Article  CAS  Google Scholar 

  16. Stephens, M. PLoS ONE 8, e65245 (2013).

    Article  CAS  Google Scholar 

  17. Lippert, C., Casale, F.P., Rakitsch, B. & Stegle, O. bioRxiv 003905 (2014).

  18. Zhou, X. & Stephens, M. Nat. Methods 11, 407–409 (2014).

    Article  CAS  Google Scholar 

  19. Price, A.L. et al. PLoS Genet. 7, e1001317 (2011).

    Article  CAS  Google Scholar 

  20. Rakitsch, B., Lippert, C., Borgwardt, K. & Stegle, O. Adv. Neur. In. 26, 1466–1474 (2013).

    Google Scholar 

  21. Price, A.L. et al. Nat. Genet. 38, 904–909 (2006).

    Article  CAS  Google Scholar 

  22. 1000 Genomes Project Consortium. et al. Nature 491, 56–65 (2012).

  23. Lippert, C. et al. Nat. Methods 8, 833–835 (2011).

    Article  CAS  Google Scholar 

  24. Sabatti, C. et al. Nat. Genet. 41, 35–46 (2009).

    Article  CAS  Google Scholar 

  25. Teslovich, T.M. et al. Nature 466, 707–713 (2010).

    Article  CAS  Google Scholar 

  26. Koishi, R. et al. Nat. Genet. 30, 151–157 (2002).

    Article  CAS  Google Scholar 

  27. Cohen, J.C. et al. Science 305, 869–872 (2004).

    Article  CAS  Google Scholar 

  28. Baud, A. et al. Nat. Genet. 45, 767–775 (2013).

    Article  CAS  Google Scholar 

  29. de Wit, H. et al. Leukemia 12, 363–370 (1998).

    Article  CAS  Google Scholar 

  30. Gilmour, A.R., Thompson, R. & Cullis, B.R. Biometrics 51, 1440–1450 (1995).

    Article  Google Scholar 

  31. Lee, S.H., Goddard, M.E., Visscher, P.M. & van der Werf, J.H. Genet. Sel. Evol. 42, 22 (2010).

    Article  Google Scholar 

  32. Stegle, O., Lippert, C., Mooij, J.M., Lawrence, N.D. & Borgwardt, K.M. Adv. Neur. Inf. 24, 630–638 (2012).

    Google Scholar 

  33. Loh, P.R. et al. Nat. Genet. 47, 284–290 (2015).

    Article  CAS  Google Scholar 

  34. Westfall, P.H., Young, S.S. & Wright, S.P. Biometrics 49, 941–945 (1993).

    Article  Google Scholar 

  35. Fusi, N., Lippert, C., Lawrence, N.D. & Stegle, O. Nat. Commun. 5, 4890 (2014).

    Article  CAS  Google Scholar 

Download references

Acknowledgements

We thank A. Baud, D. Horta and H. Kilpinen for comments on the manuscript. The NFBC1966 study is conducted and supported by the US National Heart, Lung, and Blood Institute (NHLBI) in collaboration with the Broad Institute, the University of California–Los Angeles (UCLA), University of Oulu and the National Institute for Health and Welfare in Finland. This manuscript was not prepared in collaboration with investigators of the NFBC1966 study and does not necessarily reflect the opinions or views of the NFBC1966 study investigators, the Broad Institute, UCLA, the University of Oulu, National Institute for Health and Welfare in Finland or the NHLBI.

Author information

Author notes

  1. Francesco Paolo Casale and Barbara Rakitsch: These authors contributed equally to this work.

Authors and Affiliations

  1. European Molecular Biology Laboratory, European Bioinformatics Institute, Wellcome Trust Genome Campus, Hinxton, Cambridge, UK

    Francesco Paolo Casale, Barbara Rakitsch & Oliver Stegle

  2. Microsoft Research, Los Angeles, California, USA

    Christoph Lippert

  3. Human Longevity, Inc., Mountain View, California, USA

    Christoph Lippert

Authors
  1. Francesco Paolo Casale
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Barbara Rakitsch
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Christoph Lippert
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Oliver Stegle
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

F.P.C., B.R. and O.S. developed the method. B.R. and F.P.C. performed the experiments and analyzed the data. C.L. provided analysis tools and contributed to the interpretation of results. O.S., B.R. and F.P.C. wrote the paper. O.S. designed and supervised the study.

Corresponding authors

Correspondence to Francesco Paolo Casale, Barbara Rakitsch or Oliver Stegle.

Ethics declarations

Competing interests

C.L. was employed by Microsoft while performing this research.

Integrated supplementary information

Supplementary Figure 1 Computational run time of alternative implementations of mtSet as a function of the number of traits.

Shown is the extrapolated CPU time (h) to test associations on chromosome 20, considering a total of 3,975 windows (tests), on a simulated cohort with 1,000 individuals for increasing numbers of traits. Compared are mtSet and the approximate mtSet-PC model. mtSet-naive denotes the runtime for a standard LMM package. Runtime estimates were obtained from a single core of an Intel Xeon CPU E5-2670 2.60 GHz processor.

Supplementary Figure 2 Computational run time of alternative implementations of mtSet as a function of the cohort size.

(a) Shown is the CPU time (h) to test associations on chromosome 20 (3,975 regions/tests) on a simulated cohort with increasing number of individuals and for four traits. Compared are mtSet and the approximate mtSet-PC model. Additionally, we considered a low-rank approximation where the background covariance has rank 30, which matches the number of PCs included as fixed effects in the mtSet-PC model (see Online Methods). mtSet-naive denotes the runtime for a standard LMM package, which scales cubical in the number of traits and samples. Runtime estimates were obtained on a single core of an Intel Xeon CPU E5-2670 2.60 GHz processor. (b) Shown is the average number of iterations until the optimizer converges. For larger number of samples, the likelihood gets more peaked, resulting in smaller number of iterations and thus reduced overall runtime.

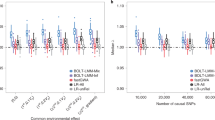
Supplementary Figure 3 Characterization of the confounding structure in the four data sets used to assess statistical calibration of mtSet.

Shown are the genetic relatedness matrices as well as scatter plots of the first two principal components for each of the four datasets used to assess the statistical calibration of mtSet. (a) Empirical genotype data of 1,000 individuals from 14 populations that are part of the 1000 genomes project (1000G). (b-d) Synthetic datasets based on 1000 genomes individuals of European ancestry. In brief, each individual is assigned to n ancestors, randomly inheriting blocks of SNPs from its ancestors. By placing alternative restrictions on the ancestors (number of ancestors, ancestors are drawn from the same or different populations), datasets with different confounding structures can be obtained: (b) simPopStructure (kinship matrix has low-rank structure), (c) simUnrelated (kinship matrix is not structured) and (d) simRelated (kinship matrix is highly structure). See Online Methods and Supplementary Note for full details.

Supplementary Figure 4 Statistical calibration of mtSet, mtSet-PC, stLMM-SV and mtLMM-SV for four data sets with different confounding structures.

Shown are QQ-plots for simulated data when only background effects (no causal variants) were simulated and when considering alternative degrees of population structure and relatedness (Online Methods; see also Supplementary Fig. 3). Compared are a single trait single-variant LMM (stLMM-SV), a multi-trait single-variant LMM (mtLMM-SV) as well as mtSet and the PC-based approximation without relatedness component (mtSet-PC).

From left to right: mtSet, mtSet-PC, stLMM-SV and mtLMM-SV.
From top to bottom: 1000 genomes (real genotypes), simPopStructure, simUnrelated and simRelated (see Supplementary Fig. 3). Whereas the models mtSet, stLMM-SV and mtLMM-SV yield robust results irrespective of the type of confounding (see also Fig. 1), mtSet-PC is not able to correct for complex (cyptic) relatedness between individuals (bottom row, second column).

Supplementary Figure 5 Parametric fit of the null distribution on simulated data using 1000 Genomes genotypes for mtSet.

The null distribution is fit by a mixture π of χ20 and a χ2d test statistics using five genome-wide permutations. Although, we use only the top 10% of null test statistics for fitting the free parameters π, a, d, we found empirically that our fit works well for the complete range of the test statistics. Shown are the results for five different repetitions of four simulated phenotypes when only background effects are present.

Supplementary Figure 6 Power comparison of alternative methods on simulated data using genotype data from 1000 Genomes individuals.

Shown is power at 10% family-wise error rate for mtSet, mtSet-PC, mtLMM-SV, stSet and stLMM-SV for varying different simulation parameters. Specifically, we altered the proportions of variance explained by the region (h2r), the numbers of causal variants in the region (Sr), the percentages of shared causal variants (πr), the proportions of variance explained by genetic background (h2g), the percentage of residual variance explained by hidden confounders (λ), and the percentage of background and residual signal that is shared across traits (α) (see also Supplementary Table 2). See Online Methods for details on the simulation procedure and the evaluation scheme.

Supplementary Figure 7 Power comparison when varying the size of the set component on simulated data using genotype data from 1000 Genomes individuals.

(a) Shown is power at 10% family-wise error rate for mtSet, stSet, mtSet-PC, mtLMM-SV and stLMM-SV when varying the region size for set test approaches. While set tests are overall robust, these methods are most powerful when the region size matches the size of the simulated causal region. (b) Average squared correlation coefficient between variants within a window as a function of the window size. (c) Number of unique SNPs within testing regions as a function of the window size. When selecting the size of the testing window both linkage disequilibrium and number of SNPs within regions should be considered. Too small testing regions will lead to high LD among SNPs within windows and low number of unique SNPs, which results in limited advantages of set tests compared to single-variant LMMs. Conversely, regions that are too large result in a prohibitively large numbers of SNPs, which presents a computational burden and may lead to reduced power (a).

Supplementary Figure 8 Scalability of mtSet as a function of the number of variants in the set component.

Shown is computational time to fit a single window using mtSet (a) and mtSet-PC (b) (randomly drawn from chrom 20, 1000 genomes dataset) for windows with increasing numbers of variants. Runtimes are reported for windows of varying size (1kb-200kb) using simulated data generated using the default parameter settings (see also Supplementary Table 2).

Supplementary Figure 9 Statistical calibration of all considered methods applied to four blood lipid levels on the NFBC data set.

(a-c) QQ-plots of set tests including the relatedness component (a), approximate set tests using PC-based correction (b) and single-variant LMMs (c). Both single-trait LMMs and set test methods are calibrated, i.e. genomic control is λ(mtLMM-SV) = 0.979, λ(stLMM-SV[CRP]) = 0.995, λ(stLMM-SV[LDL]) = 0.996, λ(stLMM-SV[HDL]) = 1.001 and λ(stLMM-SV[TRIGL]) = 0.978 for the single-variant methods, λ(mtSet) = 1.001 and λ(mtSetPC) = 0.989 for the set test methods.

Supplementary Figure 10 Histogram of P values obtained from single- and multi-trait set tests applied to four blood lipid levels on the NFBC data set.

Top row: multi-trait set tests (mtSet, mtSet-PC) applied to four lipid related traits.
Bottom two rows: single-trait set test (stSet) applied to individual traits. The spike in the histograms is a common feature of set tests and results form the constrained marginal likelihood optimization: the set component is bounded to explain variance greater to or equal to zero, resulting in a box constraint optimization. The location of the spike is determined by the mixture coefficients of the parametric null distribution fit (see Online Methods and Supplementary Note).

Supplementary Figure 11 Manhattan plots for different methods applied to four blood lipid levels on the NFBC data set.

(a,b) Shown are Manhattan plots of the minimal P values across traits, considering either a single-trait single-variant LMM (stLMM-SV, (a)) or a single-trait set test (stSet (b)). (c-e) Corresponding Manhattan plots for multi-trait approaches jointly fit to all four traits, mtLMM-SV (c), mtSet (d) and mtSet-PC (e). mtSet-PC is the most powered approach and recovers all associations found by the union of QTLs retrieved by previous approaches (stLMM-SV,mtLMM-SV and stSet) and yields two additional QTLs: one association on chromosome 1 (shared with mtSet) and a second QTL on chromosome 16.

Supplementary Figure 12 Manhattan plots for quantitative traits related to basal hematology in the rat data set.

(a, c, e, g, i, k) Manhattan plots for basophils (basos), eosinophils (eos), large unstained cells (luc), lymphocytes (lymphs), monocytes (monos) and neutrophils (neuts) respectively, when using a single-trait single-variant LMM (stSet-SV). (b, d, f, h, j, l) Analogous Manhattan plots for the same traits obtained using a single-trait set test (stSet). (m, n) Manhattan plots from the multi-trait single-variant LMM (mtLMM-SV) and the multi-trait set test (mtSet) respectively. Note that the horizontal lines in Manhattan plots for stSet and mtSet are a common feature of set tests and results form the constrained marginal likelihood optimization: the set component is bounded to explain variance greater to or equal to zero, resulting in a box constraint optimization (see also Supplementary Fig. 10).

Supplementary Figure 13 Manhattan plots for set tests when considering different strategies for confounder correction applied to six phenotypes related to basal hematology in the rat data set.

(a) Manhattan plot obtained when applying mtSet without any adjustment for relatedness or population structure (mtSet-noBg). (b) Equivalent Manhattan plot when using principal components to correct for population structure (mtSet-PC). (c) Results obtained from the full mtSet model, where relatedness is accounted for using a second random effect term. Because of the closely related individuals in the study population, only the full mtSet model is able to comprehensively correct for relatedness (c); see also main Fig. 2.

Supplementary Figure 14 Distribution of the number of variants within testing regions as well as the squared intra-SNP correlation coefficient, when considering regions of increasing window sizes.

Left column: Dependency between region sizes and the number of contained variants. Right column: Dependency between the region sizes and SNP-SNP squared correlation coefficient for SNPs within regions. From top to bottom: Rat datasets, NFBC data, 1000 genomes data (chromosome 20). The computational cost of mtSet depends on the number of (unique) SNPs in testing regions. In the experiments, we considered 100kb windows for the NFBC data, 1mb windows for the rat study and 30kb windows for the 1000 genomes data. Alternative results for different region sizes are shown in Supplementary Fig. 7 (simulated data based on 1000 genomes individuals) and Supplementary Table 4 (NFBC data).

Supplementary Figure 15 Comparison of test P values obtained from mtSet-PC and mtSet-LowRankBg.

Compared are likelihood ratio test statistics for the mtSet-PC model and a model that considers a low-rank approximation to the background covariance (using the same number of principal components, mtSet-LowRankBg, Online Methods). For large cohorts, we observe good concordance between both models. This confirms that accounting for PCs as (REML) fixed effects or alternatively including them as random effect covariates yields concordant results.

Supplementary information

Supplementary Text and Figures

Supplementary Figures 1–15, Supplementary Tables 1, 2, 6 and 7, and Supplementary Note (PDF 2629 kb)

Supplementary Table 3

Tabular summary of QTLs identified by different set tests and single-variant LMMs on the NFBC dataset. (XLSX 61 kb)

Supplementary Table 4

Tabular summary of QTLs identified by mtSet when varying the region size on the NFBC dataset. (XLSX 44 kb)

Supplementary Table 5

Tabular summary of QTLs identified by different set tests and single-variant LMMs on the rat dataset. (XLSX 13 kb)

Supplementary Software

mtSet software (ZIP 2412 kb)

Source data

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Casale, F., Rakitsch, B., Lippert, C. et al. Efficient set tests for the genetic analysis of correlated traits. Nat Methods 12, 755–758 (2015). https://doi.org/10.1038/nmeth.3439

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nmeth.3439

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing