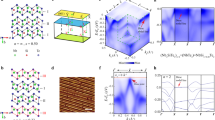
Abstract
Transition-metal dichalcogenides (TMDs) are renowned for their rich and varied bulk properties, while their single-layer variants have become one of the most prominent examples of two-dimensional materials beyond graphene. Their disparate ground states largely depend on transition metal d-electron-derived electronic states, on which the vast majority of attention has been concentrated to date. Here, we focus on the chalcogen-derived states. From density-functional theory calculations together with spin- and angle-resolved photoemission, we find that these generically host a co-existence of type-I and type-II three-dimensional bulk Dirac fermions as well as ladders of topological surface states and surface resonances. We demonstrate how these naturally arise within a single p-orbital manifold as a general consequence of a trigonal crystal field, and as such can be expected across a large number of compounds. Already, we demonstrate their existence in six separate TMDs, opening routes to tune, and ultimately exploit, their topological physics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Young, S. M. et al. Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012).
Liu, Z. K. et al. Discovery of a three-dimensional topological Dirac semimetal Na3Bi. Science 343, 864–867 (2014).
Wang, Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B. 85, 195320 (2012).
Wang, Z. et al. Three-dimensional Dirac semimetal and quantum transport in Cd3As2 . Phys. Rev. B 88, 125427 (2013).
Borisenko, S. et al. Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014).
Yang, B.-J. & Nagaosa, N. et al. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nat. Commun. 5, 4898 (2014).
Yang, B.-J., Morimoto, T. & Furusaki, A. Topological charges of three-dimensional Dirac semimetals with rotation symmetry. Phys. Rev. B 92, 165120 (2015).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Yang, L. X. et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 11, 728–732 (2015).
Lv, B. Q. et al. Observation of Weyl nodes in TaAs. Nat. Phys. 11, 724–727 (2015).
Wan, X. et al. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Weng, H. et al. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Borisenko, S. et al. Time-reversal symmetry breaking type-II Weyl state in YbMnBi2. Preprint at http://arxiv.org/abs/1507.04847 (2016).
Huang, L. et al. Spectroscopic evidence for a type II Weyl semimetallic state in MoTe2 . Nat. Mater. 15, 1155–1160 (2016).
Deng, K. et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2 . Nat. Phys. 12, 1105–1110 (2016).
Tamai, A. et al. Fermi arcs and their topological character in the candidate type-II Weyl semimetal MoTe2 . Phys. Rev X 6, 031021 (2016).
O’Brien, T .E., Diez, M. & Beenakker, C. W. J. Magnetic breakdown and Klein tunneling in a type-II Weyl semimetal. Phys. Rev. Lett. 116, 236401 (2016).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495–498 (2015).
Xu, Y. et al. Structured Weyl points in spin-orbit coupled fermionic superfluids. Phys. Rev. Lett. 115, 265304 (2015).
McCormick, T .M., Kimchi, I. & Trivedi, N. Minimal models for topological Weyl semimetals. Phys. Rev. B 95, 075133 (2017).
Xiong, J. et al. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 350, 413–416 (2015).
Gooth, J. et al. Experimental signatures of the mixed axial–gravitational anomaly in the Weyl semimetal NbP. Nature 547, 324–327 (2017).
Ferreiros, Y., Zyuzin, A. A. & Bardarson, J. H. Anomalous Nernst and thermal Hall effects in tilted Weyl semimetals. Phys. Rev. B 96, 115202 (2017).
Saha, S. & Tewari, S. Anomalous Nernst effect in type-II Weyl semimetals. Preprint at http://arxiv.org/abs/1707.04117 (2017).
McCormick, T. M., McKay, R. C. & Trivedi, N. The semiclassical theory of anomalous transport in type-II topological Weyl semimetals. Preprint at http://arxiv.org/abs/1707.06222 (2017).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Belopolski, I. et al. Criteria for directly detecting topological Fermi arcs in Weyl semimetals. Phys. Rev. Lett. 116, 066802 (2016).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N. & Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nano. 7, 669–712 (2012).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013).
Raub, C. J. et al. The occurrence of superconductivity in sulfides, selenides, tellurides of Pt-group metals. J. Phys. Chem. Solids 26, 2051–2057 (1965).
Noh, H.-J. et al. Experimental realization of type-II Dirac fermions in a PdTe2 superconductor. Phys. Rev. Lett. 119, 016401 (2017).
Fei, F. et al. Nontrivial Berry phase and type II Dirac transport in layered material PdTe2 . Phys. Rev. B 96, 041201(R) (2017).
Yan, L. et al. Identification of topological surface state in PdTe2 superconductor by angle-resolved photoemission spectroscopy. Chin. Phys. Lett. 32, 067303 (2015).
Xu, S.-Y. et al. Observation of Fermi arc surface states in a topological metal. Science 347, 294–298 (2015).
Yi, H. et al. Evidence of topological surface state in three-dimensional Dirac semimetal Cd3As2 . Sci. Rep. 4, 6106 (2014).
Chang, T.-R. et al. Type-II topological Dirac semimetals: theory and materials prediction (VAl3 family). Preprint at http://arxiv.org/abs/1606.07555 (2016).
Zhang, P. et al. A precise method for visualizing dispersive features in image plots. Rev. Sci. Instrum. 82, 043712 (2011).
Guo, G. Y. & Liang, W. Y. The electronic structures of platinum dichalcogenides: PtS2, PtSe2 and PtTe2 . J. Phys. C: Solid State Phys. 19, 995–1008 (1986).
Yan, M. et al. Lorentz-violating type-II Dirac fermions in transition metal dichalcogenide PtTe2 . Nat. Commun. 8, 257 (2017).
Huang, H., Zhou, S. & Duan, W. Type-II Dirac fermions in the PtSe2 class of transition metal dichalcogenides. Phys. Rev. B. 94, 121117(R) (2016).
Cao, H. et al. Origin of the phase transition in IrTe2: structural modulation and local bonding instability. Phys. Rev. B. 88, 115122 (2013).
Fang, A. F. et al. Structural phase transition in IrTe2: a combined study of optical spectroscopy and band structure calculations. Sci. Rep. 3, 1153 (2013).
Riley, J. M. et al. Direct observation of spin-polarized bulk bands in an inversion-symmetric semiconductor. Nat. Phys. 10, 835–839 (2014).
Riley, J. M. et al. Negative electronic compressibility and tunable spin splitting in WSe2 . Nat. Nano. 10, 1043–1047 (2015).
Wilson, J. A., Di Salvo, F. J. & Mahajan, S. Charge-density waves in metallic layered transition-metal dichalcogenides. Phys. Rev. Lett. 32, 882–885 (1974).
Borisenko, S. V. et al. Pseudogap and charge density waves in two dimensions. Phys. Rev. Lett. 100, 196402 (2008).
Yokoya, T. et al. Fermi surface sheet-dependent superconductivity in 2H-NbSe2 . Science 294, 2518–2520 (2001).
Bawden, L. et al. Spin-valley locking in the normal state of a transition-metal dichalcogenide superconductor. Nat. Commun. 7, 11711 (2016).
Balaha, P. et al. WIEN2K package, Version 13.1 (2013).
Souza, I. et al. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B. 65, 035109 (2001).
Mostofi, A. A. et al. Wannier90: a tool for obtaining maximally localized Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Kunes, J. et al. WIEN2WANNIER: from linearized augmented plane waves to maximally localized Wannier functions. Comput. Phys. Commun. 181, 1888–1895 (2010).
Salter, J. C. & Koster, G. F. Simplified LCAO method for the periodic potential problem. Phys. Rev. 94, 1498–1524 (1954).
Bigi, C. et al. Very efficient spin polarization analysis (VESPA): new exchange scattering-based setup for spin-resolved ARPES at APE-NFFA beamline at Elettra. J. Synchrotron Radiat. 24, 750–756 (2017).
Acknowledgements
We thank R. Arita and N. Nagaosa for useful discussions and feedback and F. Bertran and P. Le Fèvre for ongoing technical support of the CASIOPEE beam line at SOLEIL. We gratefully acknowledge support from the CREST, JST (Nos JPMJCR16F1 and JPMJCR16F2), the Leverhulme Trust, the Engineering and Physical Sciences Research Council, UK (Grant Nos EP/M023427/1 and EP/I031014/1), the Royal Society, the Japan Society for Promotion of Science (Grant-in-Aid for Scientific Research (S); No. 24224009 and (B); No. 16H03847), the International Max-Planck Partnership for Measurement and Observation at the Quantum Limit, Thailand Research Fund and Suranaree University of Technology (Grant No. BRG5880010) and the Research Council of Norway through its Centres of Excellence funding scheme, project number 262633, QuSpin, and through the Fripro program, project number 250985 FunTopoMat. This work has been partly performed in the framework of the nanoscience foundry and fine analysis (NFFA-MIUR Italy, Progetti Internazionali) facility. B.-J. Y. was supported by the Institute for Basic Science in Korea (Grant No. IBS-R009-D1), Research Resettlement Fund for the new faculty of Seoul National University, and Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (Grant No. 0426-20150011). O.J.C., L.B., J.M.R. and V.S. acknowledge EPSRC for PhD studentship support through grant Nos EP/K503162/1, EP/G03673X/1, EP/L505079/1 and EP/L015110/1. I.M. acknowledges PhD studentship support from the IMPRS for the Chemistry and Physics of Quantum Materials. We thank Diamond Light Source (via Proposal Nos SI9500, SI12469, SI13438 and SI14927) Elettra, SOLEIL, and Max-Lab synchrotrons for access to Beamlines I05, APE, CASSIOPEE, and i3, respectively, that contributed to the results presented here.
Author information
Authors and Affiliations
Contributions
M.S.B. and B.J.Y. performed the theoretical calculations. The experimental data were measured by O.J.C., J.Feng, L.B., J.M.R., I.M., F.M., V.S., D.B., S.P.C., M.J., J.W.W., T.E., W.M. and P.D.C.K, and analysed by O.J.C.; M.L., T.B., J.Fujii, I.V., J.E.R., T.K.K. and M.H. maintained the ARPES/spin-resolved ARPES end stations and provided experimental support. K.O., M.A. and T.S. synthesized the measured samples. P.D.C.K., O.J.C. and M.S.B. wrote the manuscript with input and discussion from co-authors. P.D.C.K. and M.S.B. were responsible for overall project planning and direction.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1508 kb)
Rights and permissions
About this article
Cite this article
Bahramy, M., Clark, O., Yang, BJ. et al. Ubiquitous formation of bulk Dirac cones and topological surface states from a single orbital manifold in transition-metal dichalcogenides. Nature Mater 17, 21–28 (2018). https://doi.org/10.1038/nmat5031
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat5031
This article is cited by
-
Investigating the role of undercoordinated Pt sites at the surface of layered PtTe2 for methanol decomposition
Nature Communications (2024)
-
Realization of practical eightfold fermions and fourfold van Hove singularity in TaCo2Te2
npj Quantum Materials (2023)
-
Evidence for unconventional superconductivity and nontrivial topology in PdTe
Scientific Reports (2023)
-
Hidden spin-orbital texture at the \(\overline{{{\Gamma }}}\)-located valence band maximum of a transition metal dichalcogenide semiconductor
Nature Communications (2022)
-
Stabilization mechanism of molecular orbital crystals in IrTe2
Communications Physics (2022)