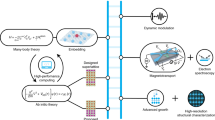
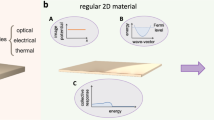
Abstract
The synthesis of bulk crystals, thin films and nanostructures plays a seminal role in expanding the frontiers of quantum materials. Crystal growers accomplish this by creating materials aimed at harnessing the complex interplay between quantum wavefunctions and various factors such as dimensionality, topology, Coulomb interactions and symmetry. This Review provides a synthesis perspective on how this discovery of quantum materials takes place. After introducing the general paradigms that arise in this context, we provide a few examples to illustrate how thin-film growers in particular exploit quantum confinement, topology, disorder and interfacial heterogeneity to realize new quantum materials.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Basic Research Needs Workshop on Quantum Materials for Energy Relevant Technology (US Department of Energy, 2016); https://science.energy.gov/∼/media/bes/pdf/reports/2016/BRNQM_rpt_Final_12-09-2016.pdf
von Klitzing, K., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Tsui, D. C., Stormer, H. L. & Gossard A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).
Bednorz, J. G. & Muller, K. A. Possible high-TC superconductivity in the Ba–La–Cu–O system. Z. Phys. B 64, 189–193 (1986).
Mackenzie, A. P. & Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 75, 657–712 (2003).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Chang, C. Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Ohtomo, A. & Hwang, H. Y. A high mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Reyren, N. et al. Superconducting interfaces between insulating oxides. Science 317, 1196–1199 (2007).
Brinkman, A. et al. Magnetic effects at the interface between non-magnetic oxides. Nat. Mater. 6, 493–496 (2007).
Li, L., Richter, C., Mannhart, J. & Ashoori, R. C. Coexistence of magnetic order and two-dimensional superconductivity at LaAlO3/SrTiO3 interfaces. Nat. Phys. 7, 762–766 (2011).
Bert, J. A. et al. Direct imaging of the coexistence of ferromagnetism and superconductivity at the LaAlO3/SrTiO3 interface. Nat. Phys. 7, 767–771 (2011).
Wang, Q. Y. et al. Interface induced high temperature superconductivity in single unit-cell FeSe films on SrTiO3 . Chin. Phys. Lett. 29, 037402 (2012).
Ge, J. F. et al. Superconductivity above 100 K in single layer FeSe films on doped SrTiO3 . Nat. Mater. 14, 285–289 (2015).
Imada, M., Fujimori, A. & Tokura, Y. Metal–insulator transitions. Rev. Mod. Phys. 70, 1039–1263 (1998).
Shimizu, Y. et al. Spin liquid state in an organic Mott insulator with a triangular lattice. Phys. Rev. Lett. 91, 107001 (2003).
Keller, H. Bussmann-Holder, A. & Müller, K. A. Jahn–Teller physics and high TC superconductivity. Mater. Today 11, 38–46 (September, 2008).
Dingle, R., Stormer, H. L. & Gossard, A. C. Electron mobilities in modulation-doped semiconductor heterojunction superlattices. Appl. Phys. Lett. 33, 665–667 (1978).
Weisbuch, C. Quantum Semiconductor Structures: Fundamentals and Applications (Academic, 1991).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X. L. & Zhang, S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Basov, D. N., Averitt, R. D. & Hsieh D. Controlling the properties of quantum materials. Nat. Mater. 16, 1078–1089 (2017).
Moler, K. A. Imaging quantum materials. Nat. Mater. 16, 1049–1052 (2017).
Keimer, B. & Moore, J. E. The physics of quantum materials. Nat. Phys. http://doi.org/10.1038/nphys4302 (2017).
Tokura, Y., Kawasaki, M. & Nagaosa, N. Emergent functions of quantum materials. Nat. Phys. http://doi.org/10.1038/nphys4274 (2017).
Gedik, N. & Vishik, I. Photoemission of quantum materials. Nat. Phys. http://doi.org/10.1038/nphys4273 (2017).
Gardner, G. C., Fallahi, S., Watson, J. D. & Manfra, M. J. Modified MBE hardware and techniques and role of gallium purity for attainment of two dimensional electron gas mobility > 35 × 106 cm2/V.s in AlGaAs/GaAs quantum wells grown by MBE. J. Cryst. Growth 441, 71–77 (2016).
Pfeiffer, L. & West, K. W. The role of MBE in recent quantum Hall effect physics discoveries. Physica E 20, 57–64 (2003).
Jain, J. K. The composite fermion: a quantum particle and its quantum fluids. Phys. Today 53, 39–45 (April, 2000).
Morales, A. M. & Lieber, C. M. A laser ablation method for the synthesis of crystalline semiconductor nanowires. Science 279, 208–211 (1998).
Alivisatos, A. P. Semiconductor clusters, nanocrystals, and quantum dots. Science 271, 933–937 (1996).
Chappert, C., Fert, A., & Van Dau, Frederick Nguyen . The emergence of spin electronics in data storage. Nat. Mater. 6, 813–823 (2007).
Awschalom, D. D. & Samarth, N. Spin dynamics and quantum transport in magnetic semiconductor quantum structures. J. Magn. Magn. Mater. 200, 130–147 (1999).
MacDonald, A. H., Schiffer, P. & Samarth, N. Ferromagnetic semiconductors: moving beyond (Ga,Mn)As. Nat. Mater. 4, 195–202 (2005).
De Jongh, L. J. & Miedema, A. R. Experiments on simple magnetic model systems. Adv. Phys. 50, 947–1170 (2001).
Butler, S. Z. et al. Progress, challenges, and opportunities in two-dimensional materials beyond graphene. ACS Nano 7, 2898–2926 (2013).
Mak, K. F. & Shan, J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photon. 10, 216–226 (2016).
Lu, J. M. et al. Evidence for two-dimensional Ising superconductivity in gated MoS2 . Science 350, 1353–1357 (2015).
Xi, X. et al. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–144 (2015).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Lee, J. et al. Wafer-scale growth of single-crystal monolayer graphene on reusable hydrogen-terminated germanium. Science 344, 286–289 (2014).
Kang, K. et al. High-mobility threeatomthick semiconducting films with wafer scale homogeneity. Nature 520, 656–660 (2015).
Jariwala, D., Marks, T. J. & Hersam, M. C. Mixed-dimensional van der Waals heterostructures. Nat. Mater. 16, 170–181 (2017).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Dzero, M., Sun, K., Galitski, V. & Coleman, P. Topological Kondo insulators. Phys. Rev. Lett. 104, 106408 (2010).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Young, S. M. et al. Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Huang, S. M. et al. A Weyl fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).
Weng, H. et al. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2008).
Tanaka, Y. et al. Experimental realization of a topological crystalline insulator in SnTe. Nat. Phys. 8, 800–803 (2012).
Liu, Z. K. et al. A stable three-dimensional topological Dirac semimetal Cd3As2 . Nat. Mater. 13, 677–681 (2014).
Borisenko, S. et al. Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014).
Neupane, M. et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2 . Nat. Commun. 5, 3786 (2014).
Xu, S. Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Heremans, J. P., Cava, R. J. & Samarth, N. Tetradymites as thermoelectrics and topological insulators. Nat. Rev. Mater. 2, 17049 (2017).
Richardella, A. et al. Characterizing the structure of topological insulator thin films. APL Mater. 3, 083303 (2015).
Schreyeck, S. et al. Molecular beam epitaxy of high structural quality Bi2Se3 on lattice matched InP (111) substrates. Appl. Phys. Lett. 102, 041914 (2013).
Ren, Z. et al. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 82, 241306 (2010).
Jia, S. et al. Low carrier concentration crystals of the topological insulator Bi2Te2Se. Phys. Rev. B 84, 235206 (2011).
Arakane, T. et al. Tunable Dirac cone in the topological insulator Bi2−xSbxTe3−ySey . Nat. Commun. 3, 1639 (2011).
Xu, Y. et al. Observation of topological surface state quantum Hall effect in an intrinsic three-dimensional topological insulator. Nat. Phys. 10, 956–963 (2014).
Zhang, J. et al. Band structure engineering in (Bi1−xSbx)2Te3 ternary topological insulators. Nat. Commun. 2, 574 (2011).
Koirala, N. et al. Record surface state mobility and quantum Hall effect in topological insulator thin films via interface engineering. Nano Lett. 15, 8245–8249 (2015).
Wu, L. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 354, 1124–1127 (2016).
Arguello, C. J. et al. Quasiparticle interference, quasiparticle interactions, and the origin of the charge density wave in 2H–NbSe2 . Phys. Rev. Lett. 114, 037001 (2015).
Kobayashi, M. et al. Critical test for Altshuler–Aronov theory: evolution of the density of states singularity in double perovskite Sr2FeMoO6 with controlled disorder. Phys. Rev. Lett. 98, 246401 (2007).
Mikheev, E. et al. Tuning bad metal and non-Fermi liquid behavior in a Mott material: rare-earth nickelate thin films. Sci. Adv. 1, e1500797 (2015).
Qi, X., Hughes, T. L. & Zhang, S. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Chen, Y. L. et al. Massive Dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662 (2010).
Xu, S. Y. et al. Hedgehog spin texture and Berry's phase tuning in a magnetic topological insulator. Nat. Phys. 8, 616–622 (2012).
Sanchez-Barriga, J. et al. Nonmagnetic band gap at the Dirac point of the magnetic topological. Nat. Commun. 7, 10559 (2016).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the 'parity anomaly'. Phys. Rev. Lett. 61, 2015–2018 (1988).
Chang, C. Z. et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 14, 473–477 (2015).
Chang, C. Z. et al. Zero-Field dissipationless chiral edge transport and the nature of dissipation in the quantum anomalous Hall state. Phys. Rev. Lett. 115, 057206 (2015).
Checkelsky, J. G. et al. Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator. Nat. Phys. 10, 731–736 (2014).
Kou, X. et al. Scale-invariant quantum anomalous Hall effect in magnetic topological insulators beyond the two-dimensional limit. Phys. Rev. Lett. 113, 137201 (2014).
Bestwick, A. J. et al. Precise quantization of the anomalous Hall effect near zero magnetic field. Phys. Rev. Lett. 114, 187201 (2015).
Kandala, A. et al. Giant anisotropic magnetoresistance in a quantum anomalous Hall insulator. Nat. Commun. 6, 7434 (2015).
Liu, M. et al. Large discrete jumps observed in the transition between Chern states in a ferromagnetic topological insulator. Sci. Adv. 2, e1600167 (2016).
Lachman, E. O. et al. Visualization of superparamagnetic dynamics in magnetic topological insulators. Sci. Adv. 1, e1500740 (2015).
Winnerlein, M. et al. Epitaxy and structural properties of (V,Bi,Sb)2Te3 layers exhibiting the quantum anomalous Hall effect. Phys. Rev. Mater. 1, 011201 (2017).
Mogi, M. et al. Magnetic modulation doping in topological insulators toward higher-temperature quantum anomalous Hall effect. Appl. Phys. Lett. 107, 182401 (2015).
Tang, C. et al. Above 400-K robust perpendicular ferromagnetic phase in a topological insulator. Sci. Adv. 3, e1700307 (2017).
Mellnik, A. R. et al. Spin-transfer torque generated by a topological insulator. Nature 511, 449–451 (2014).
Fan, Y. et al. Magnetization switching through giant spin–orbit torque in a magnetically doped topological insulator heterostructure. Nat. Mater. 13, 699–704 (2014).
De Gennes, P. G. Boundary effects in superconductors. Rev. Mod. Phys. 36, 225–237 (1964).
Pannetier, B. & Courtois, H. Andreev reflection and proximity effect. J. Low Temp. Phys. 118, 599–615 (2000).
Eschrig, M. Spin-polarized supercurrents for spintronics. Phys. Today 64, 43–47 (January, 2011).
Zhang, D. M. et al. Superconducting proximity effect and possible evidence for Pearl vortices in a candidate topological insulator. Phys. Rev. B 84, 165120 (2011).
Sacépé, B. et al. Gate-tuned normal and superconducting transport at the surface of a topological insulator. Nat. Commun. 2, 575 (2011).
Hellman, F. et al. Interface-induced phenomena in magnetism. Rev. Mod. Phys. 89, 25006 (2017).
Wang, Z. et al. Proximity-Induced ferromagnetism in graphene revealed by the anomalous Hall effect. Phys. Rev. Lett. 114, 016603 (2015).
Hwang, H. Y. et al. Emergent phenomena at oxide interfaces. Nat. Mater. 11, 103–113 (2012).
Ahadi, K. & Stemmer, S. Novel metal–insulator transition at the SmTiO3/SrTiO3 interface. Phys. Rev. Lett. 118, 236803 (2017).
Yeats, A. L. et al. Persistent optical gating of a topological insulator. Sci. Adv. 1, e1500640 (2015).
Yeats, A. L. et al. Local optical control of ferromagnetism and chemical potential in a topological insulator. Proc. Natl Acad. Sci. USA 114, 10379–10383 (2017).
Lee, J. J. et al. Interfacial mode coupling as the origin of the enhancement of TC in FeSe films on SrTiO3 . Nature 515, 245–248 (2014).
Gambetta, J. M., Chow, J. M. & Steffen, M. Building logical qubits in a superconducting quantum computing system. NPJ Quant. Inf. 3, 2 (2017).
Fuechsle, M. et al. A single-atom transistor. Nat. Nano. 7, 242–246 (2012).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Majer, J. et al. Coupling superconducting qubits via a cavity bus. Nature 449, 443–447 (2007).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor–semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Andrich, P. et al. Long-range spin wave mediated control of defect qubits in nanodiamonds. NPJ Quant. Inf. 3, 28 (2017).
Ramesh, R. & Spaldin, N. A. Multiferroics: progress and prospects in thin films. Nat. Mater. 6, 21–29 (2007).
Dellas, N. et al. Electron microscopy of GaAs/MnAs core/shell nanowires. Appl. Phys. Lett. 97, 072505 (2010).
Ortmann, F., Roche, S., Valenzuela, S. O. & Molenkamp, L. W. (eds) Topological Insulators: Fundamentals and Perspectives Ch. 12 (Wiley, 2015).
Zhang, D. et al. Interplay between ferromagnetism, surface states, and quantum corrections in a magnetically doped topological insulator. Phys. Rev. B 86, 205127 (2012).
Acknowledgements
The author thanks A. Richardella and J. Kally for the unpublished atomic force microscopy and transmission electron microscopy data shown in this Review. This work is supported by the Pennsylvania State University 2D Crystal Consortium—Materials Innovation Platform (2DCC-MIP), funded through National Science Foundation Cooperative Agreement DMR-1539916. The author also acknowledges support from the National Science Foundation (DMR-1306510), the Office of Naval Research (N00014-15-1-2370, N00014-15-1-2675), the Army Research Office Multidisciplinary University Research Initiative (W911NF-12-1-0461) and C-SPIN, one of six centres of STARnet, a Semiconductor Research Corporation programme, sponsored by MARCO and DARPA.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The author declares no competing financial interests.
Rights and permissions
About this article
Cite this article
Samarth, N. Quantum materials discovery from a synthesis perspective. Nature Mater 16, 1068–1076 (2017). https://doi.org/10.1038/nmat5010
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat5010
This article is cited by
-
Macro- and atomic-scale observations of a one-dimensional heterojunction in a nickel and palladium nanowire complex
Nature Communications (2022)
-
Crystal growth of quantum materials: a review of selective materials and techniques
Bulletin of Materials Science (2022)
-
Spin current as a probe of quantum materials
Nature Materials (2020)
-
Topological nanomaterials
Nature Reviews Materials (2019)
-
Nucleation of Sodium in a Plasma Stream with Neon
Russian Physics Journal (2019)