Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Bronze-mean hexagonal quasicrystal

Nature Materials volume 16, pages 987–992 (2017)Cite this article

Subjects

Abstract

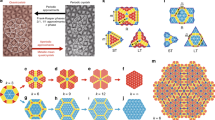
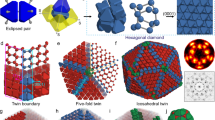
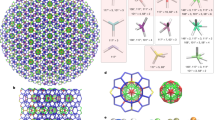
The most striking feature of conventional quasicrystals is their non-traditional symmetry characterized by icosahedral, dodecagonal, decagonal or octagonal axes1,2,3,4,5,6. The symmetry and the aperiodicity of these materials stem from an irrational ratio of two or more length scales controlling their structure, the best-known examples being the Penrose7,8 and the Ammann–Beenker9,10 tiling as two-dimensional models related to the golden and the silver mean, respectively. Surprisingly, no other metallic-mean tilings have been discovered so far. Here we propose a self-similar bronze-mean hexagonal pattern, which may be viewed as a projection of a higher-dimensional periodic lattice with a Koch-like snowflake projection window. We use numerical simulations to demonstrate that a disordered variant11 of this quasicrystal can be materialized in soft polymeric colloidal particles with a core–shell architecture12,13,14,15,16,17. Moreover, by varying the geometry of the pattern we generate a continuous sequence of structures, which provide an alternative interpretation of quasicrystalline approximants observed in several metal–silicon alloys18.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Bronze tiling.
Figure 2: Hard-core/square-shoulder random bronze quasicrystal.
Figure 3: Tile frequencies.
Figure 4: Higher-dimensional analysis.
Figure 5: Phason defects.

Similar content being viewed by others

References

  1. Levine, D. & Steinhardt, P. J. Quasicrystals: a new class of ordered structures. Phys. Rev. Lett. 53, 2477–2480 (1984).

    Article  CAS  Google Scholar 

  2. Shechtman, D., Blech, I., Gratias, D. & Cahn, J. W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53, 1951–1953 (1984).

    Article  CAS  Google Scholar 

  3. Ishimasa, T., Nissen, H.-U. & Fukao, Y. New ordered state between crystalline and amorphous in Ni-Cr particles. Phys. Rev. Lett. 55, 511–513 (1985).

    Article  CAS  Google Scholar 

  4. Tsai, A. P., Inoue, A. & Masumoto, T. A stable quasicrystal in Al–Cu–Fe system. Jpn. J. Appl. Phys. 26, L1505–L1507 (1987).

    Article  CAS  Google Scholar 

  5. Janssen, T., Chapuis, G. & de Boissieu, M. Aperiodic Crystals: From Modulated Phases to Quasicrystals (Oxford Univ. Press, 2007).

    Book  Google Scholar 

  6. Steurer, W. & Deloudi, S. Crystallography of Quasicrystals: Concepts, Methods and Structures (Springer, 2009).

    Google Scholar 

  7. Penrose, R. The role of aesthetics in pure and applied mathematical research. Bull. Inst. Math. Appl. 10, 266–271 (1974).

    Google Scholar 

  8. Mackay, A. Crystallography and the Penrose pattern. Physica A 114, 609–613 (1982).

    Article  Google Scholar 

  9. Grünbaum, B. & Shephard, G. C. Tilings and Patterns (Freeman, 1987).

    Google Scholar 

  10. Beenker, F. P. M. Algebraic theory of non-periodic tilings of the plane by two simple building blocks: a square and a rhombus. TH-Report Vol. 82-WSK04 1–64 (Eindhoven University of Technology, 1982).

  11. Oxborrow, M. & Henley, C. L. Random square-triangle tilings: a model for twelvefold-symmetric quasicrystals. Phys. Rev. B 48, 6966–6998 (1993).

    Article  CAS  Google Scholar 

  12. Zeng, X. et al. Supramolecular dendritic liquid quasicrystals. Nature 428, 157–160 (2004).

    Article  CAS  Google Scholar 

  13. Chanpuriya, S. et al. Cornucopia of nanoscale ordered phases in sphere-forming tetrablock terpolymers. ACS Nano 10, 4961–4972 (2016).

    Article  CAS  Google Scholar 

  14. Fischer, S. et al. Colloidal quasicrystals with 12-fold and 18-fold diffraction symmetry. Proc. Natl Acad. Sci. USA 108, 1810–1814 (2011).

    Article  CAS  Google Scholar 

  15. Iacovella, C. R., Keys, A. S. & Glotzer, S. C. Self-assembly of soft-matter quasicrystals and their approximants. Proc. Natl. Acad. Sci. USA 108, 20935–20940 (2011).

    Article  CAS  Google Scholar 

  16. Engel, M. & Trebin, H.-R. Self-assembly of monatomic complex crystals and quasicrystals with a double-well interaction potential. Phys. Rev. Lett. 98, 225505 (2007).

    Article  Google Scholar 

  17. Dotera, T., Oshiro, T. & Ziherl, P. Mosaic two-lengthscale quasicrystals. Nature 506, 208–211 (2014).

    Article  CAS  Google Scholar 

  18. Ishimasa, T. Dodecagonal quasicrystals still in progress. Isr. J. Chem. 51, 1216–1225 (2011).

    Article  CAS  Google Scholar 

  19. Gumbs, G. & Ali, M. K. Dynamical maps, Cantor spectra, and localization for Fibonacci and related quasiperiodic lattices. Phys. Rev. Lett. 60, 1081–1084 (1988).

    Article  CAS  Google Scholar 

  20. Suzuki, T.-K. & Dotera, T. Dynamical systems for quasiperiodic chains and new self-similar polynomials. J. Phys. A: Math. Gen. 26, 6101–6113 (1993).

    Article  Google Scholar 

  21. Buitrago, A. R. Polygons, diagonals, and the bronze mean. Nexus Netw. J. 9, 321–326 (2008).

    Article  Google Scholar 

  22. Stampfli, P. Dodecagonal quasiperiodic lattice in two dimensions. Helv. Phys. Acta 59, 1260–1263 (1986).

    Google Scholar 

  23. Niizeki, K. A step toward an MLD classification of selfsimilar quasilattices. Prog. Theor. Phys. 128, 629–691 (2012).

    Article  Google Scholar 

  24. Socolar, J. E. S., Lubensky, T. C. & Steinhardt, P. J. Phonons, phasons, and dislocations in quasicrystals. Phys. Rev. B 34, 3345–3360 (1986).

    Article  CAS  Google Scholar 

  25. Dotera, T. & Steinhardt, P. J. Ising-like transition and phason unlocking in icosahedral quasicrystals. Phys. Rev. Lett. 72, 1670–1673 (1994).

    Article  CAS  Google Scholar 

  26. Iga, H., Mihalkovič, M. & Ishimasa, T. Approximant of dodecagonal quasicrystal formed in MnSiV alloy. Philos. Mag. 91, 2624–2633 (2011).

    Article  CAS  Google Scholar 

  27. Ishimasa, T., Iwami, S., Sakaguchi, N., Oota, R. & Mihalkovič, M. Phason space analysis and structure modelling of 100 Å-scale dodecagonal quasicrystal in Mn-based alloy. Philos. Mag. 95, 3745–3767 (2015).

    Article  CAS  Google Scholar 

  28. Förster, S. et al. Observation and structure determination of an oxide quasicrystal approximant. Phys. Rev. Lett. 117, 095501 (2016).

    Article  Google Scholar 

  29. Ye, X. et al. Quasicrystalline nanocrystal superlattice with partial matching rules. Nat. Mater. 16, 214–219 (2017).

    Article  CAS  Google Scholar 

  30. Sasisekharan, V., Baranidharan, S., Balagurusamy, V. S. K., Srinivasan, A. & Gopal, E. S. R. Non-periodic tilings in 2-dimensions with 4, 6, 8, 10 and 12-fold symmetries. Pramana J. Phys. 33, 405–420 (1989).

    Article  Google Scholar 

Download references

Acknowledgements

This project has been supported by the Japan Society for the Promotion of Science through Grant-in-Aid for Scientific (B) (No. 16H04037), and has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 642774. The authors acknowledge the financial support from the Slovenian Research Agency (research core funding No. P1-0055).

Author information

Authors and Affiliations

  1. Department of Physics, Kindai University, 3-4-1 Kowakae Higashi-Osaka 577-8502, Japan

    Tomonari Dotera & Shinichi Bekku

  2. Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, SI-1000 Ljubljana, Slovenia

    Primož Ziherl

  3. Jožef Stefan Institute, Jamova 39, SI-1000 Ljubljana, Slovenia

    Primož Ziherl

Authors
  1. Tomonari Dotera
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shinichi Bekku
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Primož Ziherl
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

T.D. and P.Z. conceived the project and proposed the tiling theory. S.B. and T.D. performed simulations and higher-dimensional analysis, and T.D. and P.Z. wrote the manuscript.

Corresponding author

Correspondence to Tomonari Dotera.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 1848 kb)

Supplementary Information

Supplementary movie 1 (MP4 6878 kb)

Supplementary Information

Supplementary movie 2 (MP4 6880 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dotera, T., Bekku, S. & Ziherl, P. Bronze-mean hexagonal quasicrystal. Nature Mater 16, 987–992 (2017). https://doi.org/10.1038/nmat4963

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nmat4963

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing