Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Programming curvature using origami tessellations

Nature Materials volume 15, pages 583–588 (2016)Cite this article

Subjects

Abstract

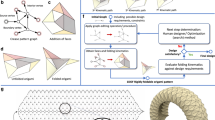
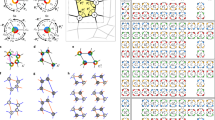
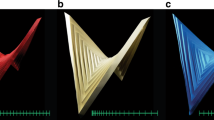
Origami describes rules for creating folded structures from patterns on a flat sheet, but does not prescribe how patterns can be designed to fit target shapes. Here, starting from the simplest periodic origami pattern that yields one-degree-of-freedom collapsible structures—we show that scale-independent elementary geometric constructions and constrained optimization algorithms can be used to determine spatially modulated patterns that yield approximations to given surfaces of constant or varying curvature. Paper models confirm the feasibility of our calculations. We also assess the difficulty of realizing these geometric structures by quantifying the energetic barrier that separates the metastable flat and folded states. Moreover, we characterize the trade-off between the accuracy to which the pattern conforms to the target surface, and the effort associated with creating finer folds. Our approach enables the tailoring of origami patterns to drape complex surfaces independent of absolute scale, as well as the quantification of the energetic and material cost of doing so.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Geometry of generalized Miura-ori.
Figure 2: Optimal calculated origami tessellations and their physical paper analogues.
Figure 3: Foldability.
Figure 4: Accuracy–effort trade-off in origami tessellations.

Similar content being viewed by others

References

  1. Demaine, E. & O’Rourke, J. Geometric Folding Algorithms: Linkages, Origami, Polyhedra (Cambridge Univ. Press, 2011).

    Google Scholar 

  2. Lang, R. Origami Design Secrets 2nd edn (CRC Press, 2011).

    Book  Google Scholar 

  3. Miura, K. Method of Packaging and Deployment of Large Membranes in Space Report No. 618 (Institute of Space and Astronautical Science, 1985).

    Google Scholar 

  4. Kobayashi, H., Kresling, B. & Vincent, J. The geometry of unfolding tree leaves. Proc. R. Soc. Lond. B 265, 147–154 (1998).

    Article  Google Scholar 

  5. Mahadevan, L. & Rica, S. Self-organized origami. Science 307, 1740 (2005).

    Article  CAS  Google Scholar 

  6. Shyer, A. et al. Villification: how the gut gets its villi. Science 342, 212–218 (2013).

    Article  CAS  Google Scholar 

  7. Bowden, N., Brittain, S., Evans, A. G., Hutchinson, J. & Whitesides, G. Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer. Nature 393, 146–149 (1998).

    Article  CAS  Google Scholar 

  8. Rizzieri, R., Mahadevan, L., Vaziri, A. & Donald, A. Superficial wrinkles in stretched, drying gelatin films. Langmuir 22, 3622–3626 (2006).

    Article  CAS  Google Scholar 

  9. Audoly, B. & Boudaoud, A. Buckling of a stiff film bound to a compliant substrate – Part III: Herringbone solutions at large buckling parameter. J. Mech. Phys. Solids 56, 2444–2458 (2008).

    Article  CAS  Google Scholar 

  10. Wei, Z. Y., Guo, Z. V., Dudte, L., Liang, H. Y. & Mahadevan, L. Geometric mechanics of periodic pleated origami. Phys. Rev. Lett. 110, 215501 (2013).

    Article  CAS  Google Scholar 

  11. Schenk, M. & Guest, S. D. Geometry of Miura-folded metamaterials. Proc. Natl Acad. Sci. USA 110, 3276–3281 (2013).

    Article  CAS  Google Scholar 

  12. Silverberg, J. L. et al. Using origami design principles to fold reprogrammable mechanical metamaterials. Science 345, 647–650 (2014).

    Article  CAS  Google Scholar 

  13. Silverberg, J. L. et al. Origami structures with a critical transition to bistability arising from hidden degrees of freedom. Nature Mater. 14, 389–393 (2015).

    Article  CAS  Google Scholar 

  14. Waitukaitis, S., Menaut, R., Chen, B. & van Hecke, M. Origami multistability: from single vertices to metasheets. Phys. Rev. Lett. 114, 055503 (2015).

    Article  Google Scholar 

  15. Tachi, T. Hangai prize papers for 2009: generalization of rigid-foldable quadrilateral-mesh origami. J. IASS 50, 173–179 (2009).

    Google Scholar 

  16. Gattas, M. & You, Z. Miura-based rigid origami: parametrizations of curved-crease geometries. J. Mech. Des. 136, 121404 (2014).

    Article  Google Scholar 

  17. Tachi, T. Origamizing polyhedral surfaces. IEEE Trans. Vis. Comput. Graphics 16, 298–311 (2010).

    Article  Google Scholar 

  18. Tachi, T. Freeform origami tessellations by generalizing Resch’s patterns. J. Mech. Des. 135, 111006 (2013).

    Google Scholar 

  19. Zhou, X., Wang, H. & You, Z. Design of three-dimensional origami structures based on vertex approach. Proc. R. Soc. A 471, 2184–2195 (2015).

    Article  Google Scholar 

  20. Castle, T. et al. Making the cut: lattice kirigami rules. Phys. Rev. Lett. 113, 245502 (2014).

    Article  Google Scholar 

  21. Sussman, D. et al. Algorithmic lattice kirigami: a route to pluripotent materials. Proc. Natl Acad. Sci. USA 112, 7449–7453 (2013).

    Article  Google Scholar 

  22. Blees, M. K. et al. Graphene kirigami. Nature 524, 204–207 (2015).

    Article  CAS  Google Scholar 

  23. Bern, M. W. & Hayes, B. The complexity of flat origami. Proc. 7th Annu (ACM-SIAM) Symp. Discrete Algorithms 175–183 (1996).

  24. Kawasaki, T. Proc. 1st Int. Meeting Origami Sci. Technol. (ed. Huzita, H.) 229–237 (1989).

    Google Scholar 

  25. Chen, Y., Peng, R. & You, Z. Origami of thick panels. Science 349, 396–400 (2015).

    Article  CAS  Google Scholar 

Download references

Acknowledgements

We thank the Harvard Microrobotics Lab for help with laser cutting; J. Weaver and O. Ahanotu for help with measuring the stress-strain behaviour of origami hypars; and the Harvard MRSEC DMR 14-20570, NSF/JSPS EAPSI 2014 (L.H.D.), NSF DMS-1304211 (E.V.), Japan Science and Technology Agency Presto (T.T.) and the MacArthur Foundation (L.M.) for partial financial support.

Author information

Authors and Affiliations

  1. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, Massachusetts 02138, USA

    Levi H. Dudte, Etienne Vouga & L. Mahadevan

  2. Graduate School of Arts and Sciences, University of Tokyo, Tokyo 153-8902, Japan

    Tomohiro Tachi

  3. Departments of Physics, and Organismic and Evolutionary Biology, Harvard University, Cambridge, Massachusetts 02138, USA

    L. Mahadevan

  4. Wyss Institute for Bio-Inspired Engineering, Harvard University, Cambridge, Massachusetts 02138, USA

    L. Mahadevan

  5. Kavli Institute for Nanobio Science and Technology, Harvard University, Cambridge, Massachusetts 02138, USA

    L. Mahadevan

Authors
  1. Levi H. Dudte
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Etienne Vouga
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tomohiro Tachi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. L. Mahadevan
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

L.H.D., E.V. and L.M. conceived and designed the research, with later contributions from T.T.; L.H.D. conducted the simulations and built the models; L.H.D., E.V. and L.M. analysed the results and wrote the manuscript.

Corresponding author

Correspondence to L. Mahadevan.

Ethics declarations

Competing interests

L.H.D., E.V. and L.M. are co-inventors of the surface-fitting algorithm and design method, patent-pending.

Supplementary information

Supplementary Information

Supplementary Information (PDF 8125 kb)

Supplementary Movie 1

Supplementary Movie 1 (MOV 3764 kb)

Supplementary Movie 2

Supplementary Movie 2 (MOV 4138 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dudte, L., Vouga, E., Tachi, T. et al. Programming curvature using origami tessellations. Nature Mater 15, 583–588 (2016). https://doi.org/10.1038/nmat4540

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nmat4540

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics