Abstract
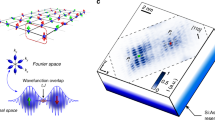
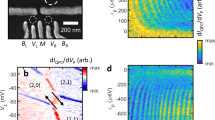
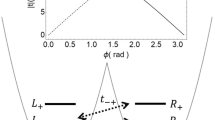
Electron and nuclear spins of donor ensembles in isotopically pure silicon experience a vacuum-like environment, giving them extraordinary coherence. However, in contrast to a real vacuum, electrons in silicon occupy quantum superpositions of valleys in momentum space. Addressable single-qubit and two-qubit operations in silicon require that qubits are placed near interfaces, modifying the valley degrees of freedom associated with these quantum superpositions and strongly influencing qubit relaxation and exchange processes. Yet to date, spectroscopic measurements have only probed wavefunctions indirectly, preventing direct experimental access to valley population, donor position and environment. Here we directly probe the probability density of single quantum states of individual subsurface donors, in real space and reciprocal space, using scanning tunnelling spectroscopy. We directly observe quantum mechanical valley interference patterns associated with linear superpositions of valleys in the donor ground state. The valley population is found to be within 5% of a bulk donor when 2.85 ± 0.45 nm from the interface, indicating that valley-perturbation-induced enhancement of spin relaxation will be negligible for depths greater than 3 nm. The observed valley interference will render two-qubit exchange gates sensitive to atomic-scale variations in positions of subsurface donors. Moreover, these results will also be of interest for emerging schemes proposing to encode information directly in valley polarization.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Morello, A. et al. Single-shot readout of an electron spin in silicon. Nature 467, 687–691 (2010).
Fuechsle, M. et al. A single-atom transistor. Nature Nanotech 7, 242–246 (2012).
Pla, J. J. et al. A single-atom electron spin qubit in silicon. Nature 489, 541–545 (2012).
Pla, J. J. et al. High-fidelity readout and control of a nuclear spin qubit in silicon. Nature 496, 334–338 (2013).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Koiller, B., Hu, X. & Das Sarma, S. Exchange in silicon-based quantum computer architecture. Phys. Rev. Lett. 88, 027903 (2001).
Wellard, C. & Hollenberg, L. Donor electron wave functions for phosphorus in silicon: Beyond effective-mass theory. Phys. Rev. B 72, 085202 (2005).
Goswami, S. et al. Controllable valley splitting in silicon quantum devices. Nature Phys. 3, 41–45 (2006).
Calderón, M., Koiller, B., Hu, X. & Das Sarma, S. Quantum control of donor electrons at the Si–SiO2 interface. Phys. Rev. Lett. 96, 096802 (2006).
Rahman, R. et al. High precision quantum control of single donor spins in silicon. Phys. Rev. Lett. 99, 036403 (2007).
Lansbergen, G. P. et al. Gate-induced quantum-confinement transition of a single dopant atom in a silicon FinFET. Nature Phys. 4, 656–661 (2008).
Saraiva, A., Calderón, M., Hu, X., Das Sarma, S. & Koiller, B. Physical mechanisms of interface-mediated intervally coupling in Si. Phys. Rev. B 80, 081305 (2009).
Morton, J. J. L., McCamey, D. R., Eriksson, M. A. & Lyon, S. A. Embracing the quantum limit in silicon computing. Nature 479, 345–353 (2011).
Yang, C. H. et al. Spin-valley lifetimes in a silicon quantum dot with tunable valley splitting. Nature Commun. 4, 2069 (2013).
Roche, B. et al. Detection of a large valley-orbit splitting in silicon with two-donor spectroscopy. Phys. Rev. Lett. 108, 206812 (2012).
Zwanenburg, F. A. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961–1019 (2013).
Roth, L. g factor and donor spin-lattice relaxation for electrons in germanium and silicon. Phys. Rev. 118, 1534–1540 (1960).
Hasegawa, H. Spin-lattice relaxation of shallow donor states in Ge and Si through a direct phonon process. Phys. Rev. 118, 1523–1534 (1960).
Gunawan, O. et al. Valley susceptibility of an interacting two-dimensional electron system. Phys. Rev. Lett. 97, 186404 (2006).
Takashina, K. et al. Impact of valley polarization on the resistivity in two dimensions. Phys. Rev. Lett. 106, 196403 (2011).
Isberg, J. et al. Generation, transport and detection of valley-polarized electrons in diamond. Nature Mater. 12, 760–764 (2013).
Young, A. F. et al. Spin and valley quantum Hall ferromagnetism in graphene. Nature Phys. 8, 550–556 (2012).
Gunawan, O., Habib, B., De Poortere, E. & Shayegan, M. Quantized conductance in an AlAs two-dimensional electron system quantum point contact. Phys. Rev. B 74, 155436 (2006).
Soykal, Ö., Ruskov, R. & Tahan, C. Sound-based analogue of cavity quantum electrodynamics in silicon. Phys. Rev. Lett. 107, 235502 (2011).
Culcer, D., Saraiva, A., Koiller, B., Hu, X. & Das Sarma, S. Valley-based noise-resistant quantum computation using Si quantum dots. Phys. Rev. Lett. 108, 126804 (2012).
Rycerz, A., Tworzydło, J. & Beenakker, C. W. J. Valley filter and valley valve in graphene. Nature Phys. 3, 172–175 (2007).
Tombros, N. et al. Quantized conductance of a suspended graphene nanoconstriction. Nature Phys. 7, 697–700 (2011).
Pei, F., Laird, E. A., Steele, G. A. & Kouwenhoven, L. P. Valley-spin blockade and spin resonance in carbon nanotubes. Nature Nanotech. 7, 630–634 (2012).
Kohn, W. & Luttinger, J. Theory of donor states in silicon. Phys. Rev. 98, 915–922 (1955).
Pantelides, S. & Sah, C. Theory of localized states in semiconductors. I. New results using an old method. Phys. Rev. B 10, 621–637 (1974).
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nature Mater. 11, 143–147 (2011).
Steger, M. et al. Quantum information storage for over 180 s using donor spins in a 28Si ‘semiconductor vacuum’. Science 336, 1280–1283 (2012).
Pitters, J. L., Piva, P. G. & Wolkow, R. A. Dopant depletion in the near surface region of thermally prepared silicon (100) in UHV. J. Vacuum Sci. Technol. B 30, 021806 (2012).
Koenraad, P. M. & Flatté, M. E. Single dopants in semiconductors. Nature Materials 10, 91–100 (2011).
Van Mieghem, P. Theory of band tails in heavily doped semiconductors. Rev. Mod. Phys. 64, 755–793 (1992).
Foxman, E. et al. Effects of quantum levels on transport through a Coulomb island. Phys. Rev. B 47, 10020–10023 (1993).
Mol, J. A., Salfi, J., Miwa, J. A., Simmons, M. Y. & Rogge, S. Interplay between quantum confinement and dielectric mismatch for ultrashallow dopants. Phys. Rev. B 87, 245417 (2013).
Sinthiptharakoon, K. et al. Investigating individual arsenic dopant atoms in silicon using low-temperature scanning tunnelling microscopy. J. Phys.: Condens. Matter 26, 012001 (2014).
Chen, C. J. Tunneling matrix elements in three-dimensional space: the derivative rule and the sum rule. Phys. Rev. B 42, 8841–8857 (1990).
Teichmann, K. et al. Controlled charge switching on a single donor with a scanning tunneling microscope. Phys. Rev. Lett. 101, 076103 (2008).
Lee, D.-H. & Gupta, J. A. Tunable field control over the binding energy of single dopants by a charged vacancy in GaAs. Science 330, 1807–1810 (2010).
Cohen, M. & Bergstresser, T. Band structures and pseudopotential form factors for fourteen semiconductors of the diamond and zinc-blende structures. Phys. Rev. 141, 789–796 (1966).
Rahman, R. et al. Engineered valley-orbit splittings in quantum-confined nanostructures in silicon. Phys. Rev. B 83, 195323 (2011).
Crommie, M. F., Lutz, C. P. & Eigler, D. M. Imaging standing waves in a 2-dimensional electron-gas. Nature 363, 524–527 (1993).
Sprunger, P. T., Petersen, L., Plummer, E., Leasgsgaard, E. & Besenbacher, F. Giant Friedel oscillations on the beryllium(0001) surface. Science 275, 1764–1767 (1997).
Rahman, R. et al. Gate-induced g-factor control and dimensional transition for donors in multivalley semiconductors. Phys. Rev. B 80, 155301 (2009).
Acknowledgements
The authors would like to thank J. Verduijn for helpful discussions. This work is supported by the European Commission Future and Emerging Technologies Proactive Project MULTI (317707) and the ARC Centre of Excellence for Quantum Computation and Communication Technology (CE110001027), and in part by the US Army Research Office (W911NF-08-1-0527). This work is part of the research program of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organization for Scientific Research (NWO). S.R. acknowledges a Future Fellowship (FT100100589). M.Y.S. acknowledges a Laureate Fellowship. The use of nanoHUB.org computational resources operated by the Network for Computational Nanotechnology funded by the US National Science Foundation under grant EEC-0228390 is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
J.S., J.A.M. and S.R. designed and conducted the experiments. R.R. performed the multi-million atom calculations. J.S., L.C.L.H. and S.R. made the key contributions to the Fourier analysis. All the authors contributed to analysis and writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 1319 kb)
Rights and permissions
About this article
Cite this article
Salfi, J., Mol, J., Rahman, R. et al. Spatially resolving valley quantum interference of a donor in silicon. Nature Mater 13, 605–610 (2014). https://doi.org/10.1038/nmat3941
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat3941
This article is cited by
-
A solid-state quantum microscope for wavefunction control of an atom-based quantum dot device in silicon
Nature Electronics (2023)
-
Hydrogenic spin-valley states of the bromine donor in 2H-MoTe2
Communications Physics (2023)
-
Optimisation of electron spin qubits in electrically driven multi-donor quantum dots
npj Quantum Information (2022)
-
Impact of the valley orbit coupling on exchange gate for spin qubits in silicon
npj Quantum Information (2022)
-
Scanning tunneling microscopy of buried dopants in silicon: images and their uncertainties
npj Computational Materials (2022)