Abstract
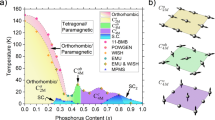
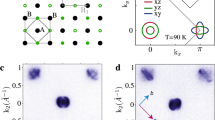
The iron chalcogenide Fe1+y(Te1−xSex) is structurally the simplest of the Fe-based superconductors1,2,3. Although the Fermi surface is similar to iron pnictides4,5, the parent compoundFe1+yTe exhibits antiferromagnetic order with an in-plane magnetic wave vector (π,0) (ref. 6). This contrasts the pnictide parent compounds where the magnetic order has an in-plane magnetic wave vector (π,π) that connects hole and electron parts of the Fermi surface7,8. Despite these differences, both the pnictide and chalcogenide Fe superconductors exhibit a superconducting spin resonance around (π,π) (refs 9, 10, 11). A central question in this burgeoning field is therefore how (π,π) superconductivity can emerge from a (π,0) magnetic instability12. Here, we report that the magnetic soft mode evolving from the (π,0)-type magnetic long-range order is associated with weak charge carrier localization. Bulk superconductivity occurs as magnetic correlations at (π,0) are suppressed and the mode at (π, π) becomes dominant for x>0.29. Our results suggest a common magnetic origin for superconductivity in iron chalcogenide and pnictide superconductors.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Hsu, F. C. et al. Superconductivity in the PbO-type structure α-FeSe. Proc. Natl Acad. Sci. USA 105, 14262–14264 (2008).
Fang, M. H. et al. Superconductivity close to magnetic instability in Fe(Se1−xTex)0.82 . Phys. Rev. B 78, 224503 (2008).
Medvedev, S. et al. Electronic and magnetic phase diagram of β-Fe1.01Se with superconductivity at 36.7 K under pressure. Nature Mater. 8, 630–633 (2009).
Subedi, A., Zhang, L. J., Singh, D. J. & Du, M. H. Density functional study of FeS, FeSe, and FeTe: Electronic structure, magnetism, phonons, and superconductivity. Phys. Rev. B 78, 134514 (2008).
Xia, Y. et al. Fermi surface topology and low-lying quasiparticle dynamics of parent Fe1+xTe/Se superconductor. Phys. Rev. Lett. 103, 037002 (2009).
Bao, W. et al. Tunable (δπ, δπ)-type antiferromagnetic order in α-Fe(Te, Se) superconductors. Phys. Rev. Lett. 102, 247001 (2009).
de la Cruz, C. et al. Magnetic order close to superconductivity in the iron-based layered LaO1−xFxFeAs systems. Nature 453, 899–902 (2008).
Huang, Q. et al. Neutron-diffraction measurements of magnetic order and a structural transition in the parent BaFe2As2 compound of FeAs-based high-temperature superconductors. Phys. Rev. Lett. 101, 257003 (2008).
Christianson, A. D. et al. Unconventional superconductivity in Ba0.6K0.4Fe2As2 from inelastic neutron scattering. Nature 456, 930–932 (2008).
Lumsden, M. D. et al. Two-dimensional resonant magnetic excitation in BaFe1.84Co0.16As2 . Phys. Rev. Lett. 102, 107005 (2009).
Qiu, Y. M. et al. Spin gap and resonance at the nesting wave vector in superconducting FeSe0.4Te0.6 . Phys. Rev. Lett. 103, 067008 (2009).
Balatsky, A. V. & Parker, D. Not all iron superconductors are the same. Physics 2, 59 (2009).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-based layered superconductor La[O1−xFx]FeAs (x=0.05–0.12) with TC=26 K. J. Am. Chem. Soc. 130, 3296–3297 (2008).
Takahashi, H. et al. Superconductivity at 43 K in an iron-based layered compound LaO1−xFxFeAs. Nature 453, 376–378 (2008).
Chen, X. H., Wu, T., Wu, G., Liu, R. H. & Fang, D. F. Superconductivity at 43 K in SmFeAsO1−xFx . Nature 453, 761–762 (2008).
Rotter, M., Tegel, M. & Johrendt, D. Superconductivity at 38 K in the iron arsenide (Ba1−xKx)Fe2As2 . Phys. Rev. Lett. 101, 107006 (2008).
Mazin, I. I., Singh, D. J., Johannes, M. D. & Du, M. H. Unconventional superconductivity with a sign reversal in the order parameter of LaFeAsO1−xFx . Phys. Rev. Lett. 101, 057003 (2008).
Chubukov, A. V., Efremov, D. V. & Eremin, I. Magnetism, superconductivity, and pairing symmetry in iron-based superconductors. Phys. Rev. B 78, 134512 (2008).
Maier, T. A., Graser, S., Scalapino, D. J. & Hirschfeld, P. Neutron scattering resonance and the iron-pnictide superconducting gap. Phys. Rev. B 79, 134520 (2009).
Zhao, J. et al. Structural and magnetic phase diagram of CeFeAsO1−xFx and its relation to high-temperature superconductivity. Nature Mater. 7, 953–959 (2008).
Luetkens, H. et al. The electronic phase diagram of the LaO1−xFxFeAs superconductor. Nature Mater. 8, 305–309 (2009).
Drew, A. J. et al. Coexistence of static magnetism and superconductivity in SmFeAsO1−xFx as revealed by muon spin rotation. Nature Mater. 8, 310–314 (2009).
Chen, H. et al. Coexistence of the spin-density wave and superconductivity in Ba1−xKxFe2As2 . Europhys. Lett. 85, 17006 (2009).
Pratt, D. K. et al. Coexistence of competing antiferromagnetic and superconducting phases in the underdoped Ba(Fe0.953Co0.047)2As2 compound using X-ray and neutron scattering techniques. Phys. Rev. Lett. 103, 087001 (2009).
Liu, T. J. et al. Charge-carrier localization induced by excess Fe in the superconductor Fe1+yTe1−xSex . Phys. Rev. B 80, 174509 (2009).
Sales, B. C. et al. Bulk superconductivity at 14 K in single crystals of Fe1+yTexSe1−x . Phys. Rev. B 79, 094521 (2009).
Khasanov, R. et al. Coexistence of incommensurate magnetism and superconductivity in Fe1+ySexTe1−x . Phys. Rev. B 80, 140511 (2009).
Wen, J. et al. Short-range incommensurate magnetic order near the superconducting phase boundary in Fe1+δTe1−xSex . Phys. Rev. B 80 104506 (2009).
Lumsden, M. D. et al. Evolution of spin excitations into the superconducting state in FeTe1−xSex . Nature Phys. 6, 182–186 (2010).
Argyriou, D. N. et al. Incommensurate itinerant antiferromagnetic excitations and spin resonance in the FeTe0.6Se0.4 superconductor. Phys. Rev. B 81, 220503 (R) (2010).
McQueen, T. M. et al. Extreme sensitivity of superconductivity to stoichiometry in Fe1+δSe. Phys. Rev. B 79, 014522 (2009).
Acknowledgements
The work at Tulane is supported by the NSF under grant DMR-0645305 for materials and equipment, and the DOE under DE-FG02-07ER46358 for personnel. Work at AMRI was supported by DARPA through grant HR 0011-09-1-0047. Work at NIST is in part supported by the NSF under grant DMR-0454672. Work at the Johns Hopkins University Institute for Quantum Matter is supported by the DOE under grant DE-FG02-08ER46544. D.N.A. and K.P. acknowledge the Deutsche Forschungsgemeinschaft for support under the priority program SPP 1458 and contract AR 613/1-2.
Author information
Authors and Affiliations
Contributions
T.J.L, J.H., B.Q., D.F. and Z.Q.M. carried out sample growth, transport property and specific heat measurements (T.J.L and J.H. contributed equally). Neutron scattering measurements were carried out by W.B., M.R., S.A.J.K., K.P., S.M., D.N.A., A.H., Y.Q., V.T., A.T.S., J.A.R. and C.B. Magnetic susceptibility was measured by A.R., H.P. and L.S.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 605 kb)
Rights and permissions
About this article
Cite this article
Liu, T., Hu, J., Qian, B. et al. From (π,0) magnetic order to superconductivity with (π,π) magnetic resonance in Fe1.02Te1−xSex. Nature Mater 9, 718–720 (2010). https://doi.org/10.1038/nmat2800
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat2800
This article is cited by
-
Kondo interaction in FeTe and its potential role in the magnetic order
Nature Communications (2023)
-
Nematic fluctuations in an orbital selective superconductor Fe1+yTe1−xSex
Communications Physics (2023)
-
Resurgence of superconductivity and the role of dxy hole band in FeSe1−xTex
Communications Physics (2023)
-
Preparation of spatially uniform monolayer FeSexTe1−x (0 < x ≤ 1) by topotactic reaction
Nano Research (2023)
-
Effects of Te- and Fe-doping on the superconducting properties in FeySe1−xTex thin films
Scientific Reports (2022)