Abstract
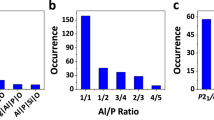
Our systematic enumeration1 of 4-connected crystalline networks (that is, networks in which each atom is connected to exactly four neighbours) used recent advances in tiling theory2 to evolve over 900 topologies. The results are relevant to the structures of zeolites and other silicates, aluminophosphates (AlPOs), oxides, nitrides, chalcogenides, halides, carbon networks, and even to polyhedral bubbles in foams. Given their importance as molecular sieves, ion exchangers, catalysts and catalyst supports, we have applied the results to microporous aluminosilicates and aluminophosphates (zeolites). Zeolite chemistry has to date produced 152 distinct types of structure. However, it was always clear that although many further structures can be synthesised, only a fraction of the mathematically generated networks would be chemically feasible (many are 'strained' frameworks requiring unrealistic bond lengths and bond angles), and that an effective 'filtering' process is needed to identify the most plausible frameworks. Here, we describe the use of computational chemistry methods to calculate optimized structural parameters, framework energies relative to α-quartz, volumes accessible to sorption, and X-ray diffraction patterns for systematically enumerated hypothetical 4-connected crystalline frameworks. Structures were treated as silica polymorphs with the empirical formula SiO2, and their energies were minimized.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Delgado Friedrichs, O., Dress, A.W.M., Huson, D.H., Klinowski, J. & Mackay, A.L. Systematic enumeration of crystalline networks. Nature 400, 644–647 (1999).
Dress, A.W.M., Huson, D.H. & Molnár, E. The classification of face-transitive periodic 3-dimensional tilings. Acta Crystallogr. A 49, 806–817 (1993).
Smith, J.V. & Dytrych, W.J. Nets with channels of unlimited diameter. Nature 309, 607–608 (1984).
Davis, M.E., Saldarriaga, C., Montes, C., Garces, J. & Crowder, C. A molecular sieve with 18-membered rings. Nature 331, 698–699 (1988).
Brunner, G.O. & Laves, F. Zum Problem der Koordinazionszahl. Wiss. Z. Tech. Univ. Dresden 20, 387–390 (1971).
Meier, W.M. & Moeck, H.J. The topology of three-dimensional 4-connected nets: classification of zeolite framework types using coordination sequences. J. Solid State Chem. 27, 349–355 (1979).
Smith, J.V. Topochemistry of zeolites and related materials. 1. Topology and geometry. Chem. Rev. 88, 149–182 (1988).
Grünbaum, B. Uniform tilings of 3-space. Geombinatorics 4, 49–56 (1994).
O'Keeffe, M. & Hyde, B.G. Crystal Structures I: Patterns and Symmetry (Mineralogical Association of America Monograph, Washington, DC, 1996).
Treacy, M.M.J., Randall, K.H., Rao, S., Perry, J.A. & Chadi, D.J. Enumeration of periodic tetrahedral frameworks. Z. Kristallogr. 212, 768–791 (1997).
Foster, M.D., Friedrichs, O.D., Bell, R.G., Paz, F.A.A. & Klinowski, J. Structural evaluation of systematically enumerated hypothetical uninodal zeolites. Angew. Chem. Intl Edn 42, 3896–3899 (2003).
Delgado Friedrichs, O. & O'Keeffe, M. Identification of and symmetry computation for crystal nets. Acta Crystallogr. A 59, 351–360 (2003).
Meier, W.M. & Villiger, H. The crystal structure of the synthetic zeolite L. Z. Kristallogr. 128, 352–370 (1969).
Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 93, 629–637 (1997).
Sanders, M.J., Leslie, M. & Catlow, C.R.A. Interatomic potentials for SiO2 . J. Chem. Soc. Chem. Commun. 1271–1273 (1984).
Schröder, K.P., Sauer, J., Leslie, M., Catlow, C.R.A. & Thomas, J.M. Bridging hydroxyl groups in zeolitic catalysts: a computer simulation of their structure, vibrational properties and acidity in protonated faujasites (H-Y zeolites). Chem. Phys. Lett. 188, 320–325 (1992).
Bell, R.G., Jackson, R.A. & Catlow, C.R.A. Computer simulation of the monoclinic distortion in silicalite. J. Chem. Soc. Chem. Commun. 782–783 (1990).
Akporiaye, D.E. & Price, G.D. Relative stability of zeolite frameworks from calculated energetics of known and theoretical structures. Zeolites 9, 321–328 (1989).
Henson, N.J., Cheetham, A.K. & Gale, J.D. Theoretical calculations on silica frameworks and their correlation with experiment. Chem. Mater. 6, 1647–1650 (1994).
Petrovic, I., Navrotsky, A., Davis, M.E. & Zones, S.I. Thermochemical study of the stability of frameworks in high-silica zeolites. Chem. Mater. 5, 1805–1813 (1993).
Piccione, P.M. et al. Thermochemistry of pure-silica zeolites. J. Phys. Chem. B 104, 10001–10011 (2000).
Connolly, M.L. Computation of molecular volume. J. Am. Chem. Soc. 107, 1118–1124 (1985).
Brunner, G.O. & Meier, W.M. Framework density distribution of zeolite-type tetrahedral nets. Nature 337, 146–147 (1989).
Simperler, A., Foster, M.D., Bell, R.G. & Klinowski, J. Hypothetical uninodal zeolite structures: comparison of AlPO4 and SiO2 compositions using computer simulation. J. Phys. Chem. B 108, 869–879 (2004).
Henson, N.J., Cheetham, A.K. & Gale, J.D. Computational studies of aluminum phosphate polymorphs. Chem. Mater. 8, 664–670 (1996).
Lewis, D.W., Willock, D.J., Catlow, C.R.A., Thomas, J.M. & Hutchings, G.J. De novo design of structure-directing agents for the synthesis of microporous solids. Nature 382, 604–606 (1996).
Correll, S., Oeckler, O., Stock, N. & Schnick, W. LixH12−x−y+z[P12OyN24-y]Clz - an oxonitridophosphate with a zeolite-like framework structure composed of 3-rings. Angew. Chem. Intl Edn 42, 3549–3552 (2003).
Zheng, N.F., Bu, X.G., Wang, B. & Feng, P.Y. Microporous and photoluminescent chalcogenide zeolite analogs. Science 298, 2366–2369 (2002).
Acknowledgements
We are grateful to the Engineering and Physical Sciences Research Council (EPSRC; UK) and the Leverhulme trust for support, and to the Portuguese Foundation for Science and Technology (FCT) for the PhD scholarship No. SFRH/BD/3024/2000 to F.A.A.P.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
About this article
Cite this article
Foster, M., Simperler, A., Bell, R. et al. Chemically feasible hypothetical crystalline networks. Nature Mater 3, 234–238 (2004). https://doi.org/10.1038/nmat1090
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat1090
This article is cited by
-
Energy landscapes of perfect and defective solids: from structure prediction to ion conduction
Theoretical Chemistry Accounts (2021)
-
Using symmetry to elucidate the importance of stoichiometry in colloidal crystal assembly
Nature Communications (2019)
-
Graph similarity drives zeolite diffusionless transformations and intergrowth
Nature Materials (2019)
-
Synthesis of ‘unfeasible’ zeolites
Nature Chemistry (2016)
-
In silico prediction and screening of modular crystal structures via a high-throughput genomic approach
Nature Communications (2015)