Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Stabilization of body-centred cubic iron under inner-core conditions

Nature Geoscience volume 10, pages 312–316 (2017)Cite this article

Subjects

Abstract

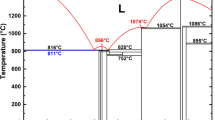
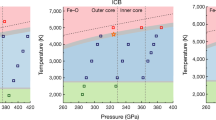
The Earth’s solid core is mostly composed of iron. However, despite being central to our understanding of core properties, the stable phase of iron under inner-core conditions remains uncertain. The two leading candidates are hexagonal close-packed and body-centred cubic (bcc) crystal structures, but the dynamic and thermodynamic stability of bcc iron under inner-core conditions has been challenged. Here we demonstrate the stability of the bcc phase of iron under conditions consistent with the centre of the core using ab initio molecular dynamics simulations. We find that the bcc phase is stabilized at high temperatures by a diffusion mechanism that arises due to the dynamical instability of the phase at lower temperatures. On the basis of our simulations, we reinterpret experimental data as support for the stability of bcc iron under inner-core conditions. We suggest that the diffusion of iron atoms in solid state may explain both the anisotropy and the low shear modulus of the inner core.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Modelling N-point transverse acoustic phonon mode (Np) in ideal bcc Fe at 360 GPa.
Figure 2: Time evolution of the computational cell sizes during two molecular dynamics runs.
Figure 3: Results of molecular dynamics simulations in the NPT ensemble at 360 GPa and high T for different sizes of computational cells starting from the bcc and hcp structures.
Figure 4: Structure of bcc iron at 7,000 K and 360 GPa.

References

  1. Birch, F. Elasticity and constitution of the Earth’s interior. J. Geophys. Res. 57, 227–286 (1952).

    Article  Google Scholar 

  2. Dziewonski, A. M. & Anderson, D. L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981).

    Article  Google Scholar 

  3. Brown, J. M. & McQueen, R. G. Phase transitions, Grüneisen parameter, and elasticity for shocked iron between 77 GPa and 400 GPa. J. Geophys. Res. 91, 7480–7494 (1986).

    Google Scholar 

  4. Nguyen, J. H. & Holmes, N. C. Melting of iron at the physical conditions of the Earth’s core. Nature 427, 339–342 (2004).

    Article  Google Scholar 

  5. Anzellini, S., Dewaele, A., Mezouar, M., Loubeyre, P. & Morard, G. Melting of iron at Earth’s inner core boundary based on fast X-ray diffraction. Science 340, 464–466 (2013).

    Article  Google Scholar 

  6. Boehler, R. Temperatures in the Earth’s core from melting-point measurements of iron at high-static pressures. Nature 363, 534–536 (1993).

    Article  Google Scholar 

  7. Belonoshko, A. B. & Ahuja, R. Embedded-atom molecular dynamic study of iron melting. Phys. Earth Planet. Inter. 102, 171–190 (1997).

    Article  Google Scholar 

  8. Alfé, D., Gillan, M. J. & Price, G. D. The melting curve of iron at the pressures of the Earth’s core from ab initio calculations. Nature 401, 462–464 (1999).

    Article  Google Scholar 

  9. Belonoshko, A. B., Ahuja, R. & Johansson, B. Quasi-ab initio molecular dynamic study of Fe melting. Phys. Rev. Lett. 84, 3638–3641 (2000).

    Article  Google Scholar 

  10. Belonoshko, A. B. et al. Origin of the low rigidity of the Earth’s inner core. Science 316, 1603–1605 (2007).

    Article  Google Scholar 

  11. Belonoshko, A. B., Skorodumova, N. V., Rosengren, A. & Johansson, B. Elastic anisotropy of the Earth’s inner core. Science 319, 797–799 (2008).

    Article  Google Scholar 

  12. Mattesini, M. et al. Hemispheric anisotropic patterns of the Earth’s inner core. PNAS 107, 9507–9512 (2010).

    Article  Google Scholar 

  13. Hemley, R. J. & Mao, H.-K. In situ studies of iron under pressure: new windows on the Earth’s core. Int. Geol. Rev. 43, 1–30 (2001).

    Google Scholar 

  14. Mikhaylushkin, A. S. et al. Pure iron compressed and heated to extreme conditions. Phys. Rev. Lett. 99, 165505 (2007).

    Article  Google Scholar 

  15. Belonoshko, A. B. et al. Quenching of bcc-Fe from high to room temperature at high-pressure conditions: a molecular dynamics simulation. New J. Phys. 11, 093039 (2009).

    Article  Google Scholar 

  16. Nguyen, J. H. et al. Molybdenum sound velocity and shear modulus softening under shock compression. Phys. Rev. B 89, 174109 (2014).

    Article  Google Scholar 

  17. Hixson, R. S., Boness, D. A., Shaner, J. W. & Moriarty, J. A. Acoustic velocities and phase transitions in molybdenum under strong shock wave compression. Phys. Rev. Lett. 62, 637–640 (1989).

    Article  Google Scholar 

  18. Lukinov, T., Simak, S. I. & Belonoshko, A. B. Sound velocity in shock compressed molybdenum obtained by ab initio molecular dynamics. Phys. Rev. B 92, 060101(R) (2015).

    Article  Google Scholar 

  19. Tateno, S., Hirose, K., Ohishi, Y. & Tatsumi, Y. The structure of iron in Earth’s inner core. Science 330, 359–362 (2010).

    Article  Google Scholar 

  20. Dubrovinsky, L., Dubrovinskaia, N. & Prakapenka, V. Is iron at the Earth’s core conditions hcp-structured? Fisica de la Terra 23, 73–82 (2011).

    Google Scholar 

  21. Belonoshko, A. B., Ahuja, R. & Johansson, B. Stability of the body-centered-cubic phase of iron in the Earth’s inner core. Nature 424, 1032–1034 (2003).

    Article  Google Scholar 

  22. Vocadlo, L., Alfé, D. & Price, G. D. Possible thermal and chemical stabilization of body-centered-cubic iron in the Earth’s core. Nature 424, 536–539 (2003).

    Article  Google Scholar 

  23. Ross, M., Young, D. A. & Grover, R. Theory of the iron phase diagram at earth core conditions. J. Geophys. Res. 95, 21713–21716 (1990).

    Article  Google Scholar 

  24. Godwal, B. K., Gonzales-Cataldo, F., Verma, A. K., Stixrude, L. & Jeanloz, R. Stability of iron crystal structures at 0.3–1.5 TPa. Earth Planet. Sci. Lett. 409, 299–306 (2015).

    Article  Google Scholar 

  25. Nishitani, S. R., Kawabe, H. & Aoki, M. First-principles calculations on bcc-hcp transition of titanium. Mater. Sci. Eng. A312, 77–83 (2001).

    Article  Google Scholar 

  26. Petry, W. et al. Phonon dispersion of the bcc phase of group-IV metals. I. bcc titanium. Phys. Rev. B 43, 10933–10947 (1991).

    Article  Google Scholar 

  27. Petry, W. et al. Phonon dispersion of the bcc phase of group-IV metals. II. bcc zirconium, a model case of dynamical precursors of martensitic transitions. Phys. Rev. B 43, 10948–10961 (1991).

    Article  Google Scholar 

  28. Niu, Z. W., Zeng, Z. Y., Cai, L. C. & Chen, X. R. Study of the thermodynamic stability of iron at inner core from first-principles theory combined with lattice dynamics. Phys. Earth Planet. Inter. 248, 12–19 (2015).

    Article  Google Scholar 

  29. Souvatzis, P., Eriksson, O., Katsnelson, M. I. & Rudin, S. P. The self-consistent ab initio lattice dynamical method. Comp. Mater. Sci. 44, 888–894 (2009).

    Article  Google Scholar 

  30. Deguen, R. Structure and dynamics of Earth’s inner core. Earth Planet. Sci. Lett. 333–334, 211–225 (2012).

    Article  Google Scholar 

  31. Romanowicz, B. et al. Seismic anisotropy in the Earth’s innermost inner core: testing structural models against mineral physics predictions. Geophys. Res. Lett. 43, 93–100 (2016).

    Article  Google Scholar 

  32. Ping, Y. et al. Solid iron compressed up to 560 GPa. Phys. Rev. Lett. 111, 065501 (2013).

    Article  Google Scholar 

  33. Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).

    Article  Google Scholar 

  34. Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).

    Article  Google Scholar 

  35. Kresse, G. & Hafner, J. Ab-initio molecular-dynamics for open-shell transition-metals. Phys. Rev. B 48, 13115–13118 (1993).

    Article  Google Scholar 

  36. Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).

    Article  Google Scholar 

  37. Wang, Y. & Perdew, J. P. Correlation hole of the spin-polarized electron-gas, with exact small-wave-vector and high-density scaling. Phys. Rev. B 44, 13298–13307 (1991).

    Article  Google Scholar 

  38. Perdew, J. P. et al. Atoms, molecules, solids, and surfaces- applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46, 6671–6687 (1992).

    Article  Google Scholar 

  39. Mermin, N. D. Thermal properties of the inhomogeneous electron gas. Phys. Rev. 137, A1441 (1965).

    Article  Google Scholar 

  40. Sutton, A. P. & Chen, J. Long-range Finnis–Sinclair potentials. Phil. Mag. Lett. 61, 139–146 (1990).

    Article  Google Scholar 

  41. González, D. & Davis, S. Fitting of interatomic potentials without forces: A parallel particle swarm optimization algorithm. Comput. Phys. Commun. 185, 3090–3093 (2014).

    Article  Google Scholar 

Download references

Acknowledgements

Computations were performed using the facilities provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputing Center in Linköping (Sweden). We also wish to thank the Swedish Research Council (VR) for financial support (grants 2013-5767 and 2014-4750). A.B.B., J.Z. and J.F. acknowledge funding from the National Magnetic Confinement Fusion Program of China (2015GB118000) and the China Scholarship Council. S.I.S. acknowledges Linköping Linnaeus Initiative for Novel Functional Materials (LiLi-NFM) and the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009 00971).

Author information

Authors and Affiliations

  1. Department of Theoretical Physics, Condensed Matter Theory, AlbaNova University Center, Royal Institute of Technology (KTH), 106 91 Stockholm, Sweden

    Anatoly B. Belonoshko, Timofei Lukinov & Jie Fu

  2. Key Laboratory of Materials Modification by Laser, Ion and Electron Beams, Dalian University of Technology, Ministry of Education, 116024 Dalian, China

    Jie Fu & Jijun Zhao

  3. Chilean Committee of Nuclear Energy (CCHEN), Casilla 188-D, Santiago, Chile

    Sergio Davis

  4. Department of Physics, Chemistry and Biology (IFM), Linköping University, SE-58183 Linköping, Sweden

    Sergei I. Simak

Authors
  1. Anatoly B. Belonoshko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Timofei Lukinov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jie Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jijun Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Sergio Davis
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Sergei I. Simak
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.B.B. designed the study, performed calculations and wrote the paper; T.L. performed calculations and wrote the paper; J.F. and S.D. performed calculations and discussed the paper; J.Z. discussed the paper; S.I.S. performed the calculations and wrote the paper; all authors discussed the results and contributed to paper writing.

Corresponding author

Correspondence to Anatoly B. Belonoshko.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 797 kb)

Supplementary Information

Supplementary Information (MP4 19457 kb)

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Belonoshko, A., Lukinov, T., Fu, J. et al. Stabilization of body-centred cubic iron under inner-core conditions. Nature Geosci 10, 312–316 (2017). https://doi.org/10.1038/ngeo2892

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/ngeo2892

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing