Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Perspective
  • Published:

The demise of Phobos and development of a Martian ring system

Nature Geoscience volume 8, pages 913–917 (2015)Cite this article

Subjects

Abstract

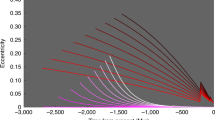
All of the gas giants in our Solar System host ring systems, in contrast to the inner planets. One proposed mechanism of planetary ring formation is disruption or mass shedding of moons. The orbit of Phobos, the larger of Mars’s two moonlets, is gradually spiralling inwards towards Mars and the moon is experiencing increasing tidal stresses. Eventually, Phobos will either break apart to form a ring or it will crash into Mars. We evaluate these outcomes based on geologic, spectral and theoretical constraints, in conjunction with a geotechnical model that helps us determine the strength of Phobos. Our analysis suggests that much of Phobos is composed of weak, heavily damaged materials. We suggest that—with continued inward migration of the moon—the weakest material will disperse tidally in 20 to 40 million years to form a Martian ring. We predict that this ring will persist for 106 to 108 years and will initially have a comparable mass density to that of Saturn’s rings. Any large fragment of Phobos that is strong enough to escape tidal breakup will eventually collide with Mars in an oblique, low-velocity impact. Our analysis of the evolution of Phobos underscores the potential orbital and topographic consequences of the growth and self-destruction of other inwardly migrating moons, including those that met their demise early in our Solar System’s history.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: The orbit of Phobos evolves inwards with time6,7.
Figure 2: Tidal stresses compete with the strength of Phobos.
Figure 3: Ultimately Phobos will either break apart or crash into Mars.
Figure 4: The expected lifetime of a Martian ring is at least 106–108 Myr.

Similar content being viewed by others

References

  1. Murray, C. D. & Dermott, S. F. Solar System Dynamics (Cambridge Univ. Press, 1999).

    Google Scholar 

  2. Canup, R. M. & Asphaug, E. Origin of the Moon in a giant impact near the end of the Earth’s formation. Nature 412, 708–712 (2001).

    Google Scholar 

  3. Goldreich, P. & Soter, S. Q in the Solar System. Icarus 5, 375–389 (1966).

    Google Scholar 

  4. Veverka, J. & Burns, J. A. The moons of Mars. Annu. Rev. Earth Planet. Sci. 8, 527–558 (1980).

    Google Scholar 

  5. Soter, S. & Harris, A. Are striations on Phobos evidence for tidal stress? Nature 268, 421–422 (1977).

    Google Scholar 

  6. Mignard, F. Evolution of the Martian satellites. Mon. Not. R. Astron. Soc. 194, 365–379 (1981).

    Google Scholar 

  7. Szeto, A. M. Orbital evolution and origin of the Martian satellites. Icarus 55, 133–168 (1983).

    Google Scholar 

  8. Bills, B. G., Neumann, G. A., Smith, D. E. & Zuber, M. T. Improved estimate of tidal dissipation within Mars from MOLA observations of the shadow of Phobos. J. Geophys. Res. 110, E07004 (2005).

    Google Scholar 

  9. Jacobson, R. A. The orbits and masses of the Martian satellites and the libration of Phobos. Astron. J. 139, 668–679 (2010).

    Google Scholar 

  10. Burns, J. A. Where are the satellites of the inner planets? Nature 242, 23–25 (1973).

    Google Scholar 

  11. Chappelow, J. & Herrick, R. On the origin of a double, oblique impact on Mars. Icarus 197, 452–457 (2008).

    Google Scholar 

  12. Canup, R. M. Origin of Saturn’s rings and inner moons by mass removal from a lost Titan-sized satellite. Nature 468, 943–926 (2010).

    Google Scholar 

  13. Pätzold, M., Andert, T., Jacobson, R., Rosenblatt, P. & Dehant, V. Phobos: Observed bulk properties. Planet. Space Sci. 102, 86–94 (2014).

    Google Scholar 

  14. Nimmo, F. & Faul, U. Dissipation at tidal and seismic frequencies in a melt-free, anhydrous Mars. J. Geophys. Res. 118, 2558–2569 (2013).

    Google Scholar 

  15. Holsapple, K. A. & Michel, P. Tidal Disruptions: II. A continuum theory for solid bodies with strength, with applications to the solar system. Icarus 193, 283–301 (2008).

    Google Scholar 

  16. Fraeman, A. et al. Analysis of disk-resolved OMEGA and CRISM spectral observations of Phobos and Deimos. J. Geophys. Res. 117, E00J15 (2012).

    Google Scholar 

  17. Rubin, A. E., Trigo-Rodríguez, J. M., Huber, H. & Wasson, J. T. Progressive aqueous alteration of CM carbonaceous chondrites. Geochim. Cosmochim. Acta 71, 2361–2382 (2007).

    Google Scholar 

  18. Willner, K., Shi, X. & Oberst, J. Phobos’ shape and topography models. Planet. Space Sci. 102, 51–59 (2014).

    Google Scholar 

  19. Richardson, D., Leinhardt, Z., Melosh, H., Bottke, W. Jr & Asphaug, E. Gravitational aggregates: Evidence and evolution. Asteroids III 1, 501–515 (2002).

    Google Scholar 

  20. Willner, K. et al. Phobos control point network, rotation, and shape. Earth Planet. Sci. Lett. 294, 541–546 (2010).

    Google Scholar 

  21. Asphaug, E. & Melosh, H. The Stickney impact of Phobos: A dynamical model. Icarus 101, 144–164 (1993).

    Google Scholar 

  22. Asphaug, E., Ostro, S., Hudson, R., Scheeres, D. & Benz, W. Disruption of kilometre-sized asteroids by energetic collisions. Nature 393, 437–440 (1998).

    Google Scholar 

  23. Rovny, J., Owen, J. M., Howley, K. & Wasem, J. in Proc. 44th Lunar Planet. Sci. Conf. 2013 1076 (LPI, 2013).

    Google Scholar 

  24. Hoek, E. & Brown, E. Practical estimates of rock mass strength. Int. J. Rock Mech. Min. Sci. 34, 1165–1186 (1997).

    Google Scholar 

  25. Hoek, E., Carranza-Torres, C. & Corkum, B. Hoek–Brown failure criterion-2002 edition. Proc. NARMS-Tac 1, 267–273 (2002).

    Google Scholar 

  26. Brown, P. G., Revelle, D. O., Tagliaferri, E. & Hildebrand, A. R. An entry model for the Tagish Lake fireball using seismic, satellite and infrasound records. Meteorit. Planet. Sci. 37, 661–675 (2002).

    Google Scholar 

  27. Colmenares, L. & Zoback, M. A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks. Int. J. Rock Mech. Min. Sci. 39, 695–729 (2002).

    Google Scholar 

  28. Leinhardt, Z. M., Ogilvie, G. I., Latter, H. N. & Kokubo, E. Tidal disruption of satellites and formation of narrow rings. Mon. Not. R. Astron. Soc. 424, 1419–1431 (2012).

    Article  Google Scholar 

  29. Colwell, J. et al. Saturn from Cassini–Huygens (eds Dougherty, M. K., Esposito, L. W. & Krimigis, S. M.) 375–412 (Springer, 2009).

    Google Scholar 

  30. Goldreich, P. & Tremaine, S. Disk–satellite interactions. Astrophys. J. 241, 425–441 (1980).

    Google Scholar 

  31. JeongAhn, Y. & Malhotra, R. The current impact flux on Mars and its seasonal variation. Icarus 262, 140–153 (2015).

    Google Scholar 

  32. Beech, M. Towards an understanding of the fall circumstances of the Hoba meteorite. Earth Moon Planets 111, 15–30 (2013).

    Google Scholar 

  33. Lee, P. et al. in Proc. 46th Lunar Planet. Sci. Conf. 2015 2856 (LPI, 2015).

    Google Scholar 

  34. Raymond, C., Prettyman, T. & Diniega, S. in Proc. 46th Lunar Planet. Sci. Conf. 2015 2792 (LPI, 2015).

    Google Scholar 

  35. Murchie, S. et al. in Proc. 46th Lunar Planet. Sci. Conf. 2015 2047 (LPI, 2015).

    Google Scholar 

  36. Kokubo, E. & Genda, H. Formation of terrestrial planets from protoplanets under a realistic accretion condition. Astrophys. J. Lett. 714, L21 (2010).

    Google Scholar 

  37. Raymond, S. N., Kokubo, E., Morbidelli, A., Morishima, R. & Walsh, K. J. in Protostars and Planets VI (eds Beuther, H. et al.) 595–618 (Univ. Arizona, Tucson, 2014).

    Google Scholar 

  38. Schofield, J. T. et al. The Mars Pathfinder atmospheric structure investigation/meteorology (ASI/MET) experiment. Science 278, 1752–1758 (1997).

    Google Scholar 

  39. Collins, G., Elbeshausen, D., Davison, T., Robbins, S. & Hynek, B. The size-frequency distribution of elliptical impact craters. Earth Planet. Sci. Lett. 310, 1–8 (2011).

    Google Scholar 

  40. Taylor, P. A. & Margot, J.-L. Tidal evolution of close binary asteroid systems. Celest. Mech. Dyn. Astron. 108, 315–338 (2010).

    Google Scholar 

  41. Goldreichand, P. & Gold, T. On the eccentricity of satellite orbits in the solar system. Mon. Not. R. Astron. Soc. 126, 257–268 (1963).

    Google Scholar 

  42. Rosenblatt, P. & Charnoz, S. On the formation of the Martian moons from a circum-Martian accretion disk. Icarus 221, 806–815 (2012).

    Google Scholar 

  43. Efroimsky, M. & Lainey, V. Physics of bodily tides in terrestrial planets and the appropriate scales of dynamical evolution. J. Geophys. Res. 112, E12003 (2007).

    Google Scholar 

  44. Auclair-Desrotour, P., Le Poncin-Lafitte, C. & Mathis, S. Impact of the frequency dependence of tidal Q on the evolution of planetary systems. Astron. Astrophys. 561, L7 (2014).

    Google Scholar 

  45. Yokoyama, T., Mana, M. R., Do Nascimento, C., Santos, M. T. & Callegari, N. Jr On the dynamics of some resonances of Phobos in the future. Astron. Astrophys. 429, 731–738 (2005).

    Google Scholar 

  46. Yokoyama, T. Possible effects of secular resonances in Phobos and Triton. Planet. Space Sci. 50, 63–77 (2002).

    Google Scholar 

  47. Peale, S. J. & Cassen, P. Contribution of tidal dissipation to lunar thermal history. Icarus 36, 245–269 (1978).

    Google Scholar 

  48. Peale, S. J., Cassen, P. & Reynolds, R. T. Melting of Io by tidal dissipation. Science 203, 892–894 (1979).

    Google Scholar 

  49. Wisdom, J. Spin–orbit secondary resonance dynamics of Enceladus. Astron. J. 128, 484–491 (2004).

    Google Scholar 

  50. Goldreich, P. & Sari, R. Tidal evolution of rubble piles. Astrophys. J. 691, 54–60 (2009).

    Google Scholar 

  51. Le Maistre, S. et al. Phobos interior from librations determination using Doppler and star tracker measurements. Planet. Space Sci. 85, 106–122 (2013).

    Google Scholar 

  52. Holsapple, K. A. Equilibrium configurations of solid cohesionless bodies. Icarus 154, 432–448 (2001).

    Google Scholar 

  53. Holsapple, K. A. & Michel, P. Tidal disruptions: A continuum theory for solid bodies. Icarus 183, 331–348 (2006).

    Google Scholar 

  54. Hoek, E. Estimating Mohr–Coulomb friction and cohesion values from the Hoek–Brown failure criterion. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 27, 227–229 (1990).

    Google Scholar 

  55. Holsapple, K. A. On the “strength” of the small bodies of the solar system: A review of strength theories and their implementation for analyses of impact disruptions. Planet. Space Sci. 57, 127–141 (2009).

    Google Scholar 

  56. Eberhardt, E. The Hoek–Brown Failure Criterion. The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring 2007–2014 233–240 (Springer, 2015).

    Google Scholar 

  57. Klimczak, C., Byrne, P. K. & Solomon, S. C. A rock-mechanical assessment of Mercury’s global tectonic fabric. Earth Planet. Sci. Lett. 416, 82–90 (2015).

    Google Scholar 

  58. Watters, T. R., Thomas, P. C. & Robinson, M. S. Thrust faults and the near-surface strength of asteroid 433 Eros. Geophys. Res. Lett. 38, L02202 (2011).

    Google Scholar 

  59. Williams, N., Watters, T, Pritchard, M., Banks, M. & Bell, J. Faults dislocation modeled structure of lobate scarps from Lunar Reconnaissance Orbiter Camera digital terrain models. J. Geophys. Res.: Planets 118, 224–233 (2013).

    Google Scholar 

  60. Jutzi, M. Sph calculations of asteroid disruptions: The role of pressure dependent failure models. Planet. Space Sci. 107, 3–9 (2015).

    Google Scholar 

  61. Mitchell, J. K., Bromwell, L. G., Carrier III, W. D., Costes, N. C. & Scott, J. F. Soil mechanical properties at the Apollo 14 site. J. Geophys. Res. 77, 5641–5664 (1972).

    Google Scholar 

  62. Lambe, T. W. & Whitman, R. V. Soil Mechanics SI Version (John Wiley, 2008).

    Google Scholar 

  63. Hoek, E. Practical Rock Engineering (2000); www.rocscience.com

  64. Cai, M. Practical estimates of tensile strength and Hoek–Brown strength parameter m i of brittle rocks. Rock Mech. Rock Eng. 43, 167–184 (2010).

    Google Scholar 

  65. Marinos, V., Marinos, P. & Hoek, E. The geological strength index: Applications and limitations. Bull. Eng. Geol. Environ. 64, 55–65 (2005).

    Google Scholar 

  66. Pajola, M. et al. Phobos as a d-type captured asteroid, spectral modeling from 0.25 to 4.0 μm. Astrophys. J. 777, 127 (2013).

    Google Scholar 

  67. Tomeoka, K. & Buseck, P. R. Indicators of aqueous alteration in cm carbonaceous chondrites: Microtextures of a layered mineral containing Fe, S, O and Ni. Geochim. Cosmochim. Acta 49, 2149–2163 (1985).

    Google Scholar 

  68. Fraeman, A. A. et al. Spectral absorptions on Phobos and Deimos in the visible/near infrared wavelengths and their compositional constraints. Icarus 229, 196–205 (2014).

    Google Scholar 

  69. Hunten, D. M. Capture of Phobos and Deimos by photoatmospheric drag. Icarus 37, 113–123 (1979).

    Google Scholar 

  70. Burns, J. A. Contradictory clues as to the origin of the Martian moons. Mars 1, 1283–1301 (1992).

    Google Scholar 

  71. Andert, T. P. et al. Precise mass determination and the nature of Phobos. Geophys. Res. Lett. 37, L09202 (2010).

    Google Scholar 

  72. Citron, R. I., Genda, H. & Ida, S. Formation of Phobos and Deimos via a giant impact. Icarus 252, 334–338 (2015).

    Google Scholar 

  73. Fanale, F. P. & Salvail, J. R. The influence of CO ice on the activity and near-surface differentiation of comet nuclei. Icarus 84, 403–413 (1990).

    Google Scholar 

  74. Popova, O. et al. Very low strengths of interplanetary meteoroids and small asteroids. Meteorit. Planet. Sci. 46, 1525–1550 (2011).

    Google Scholar 

  75. Brown, P. G. et al. The fall, recovery, orbit, and composition of the Tagish Lake meteorite: A new type of carbonaceous chondrite. Science 290, 320–325 (2000).

    Google Scholar 

  76. Hildebrand, A. R. et al. The fall and recovery of the Tagish Lake meteorite. Meteorit. Planet. Sci. 41, 407–431 (2006).

    Google Scholar 

  77. Bažant, Z. P, Kim, J.-J. H., Daniel, I. M., Becq-Giraudon, E. & Zi, G. Size effect on compression strength of fiber composites failing by kink band propagation. Int. J. Fract. 95, 103–141 (1999).

    Google Scholar 

  78. Sharma, I. The equilibrium of rubble-pile satellites: The Darwin and Roche ellipsoids for gravitationally held granular aggregates. Icarus 200, 636–654 (2009).

    Google Scholar 

  79. Dobrovolskis, A. R. Internal stresses in Phobos and other triaxial bodies. Icarus 52, 136–148 (1982).

    Google Scholar 

  80. Alejano, L. R. & Bobet, A. Drucker–Prager criterion. Rock Mech. Rock Eng. 45, 995–999 (2012).

    Google Scholar 

  81. Veras, D., Leinhardt, Z. M., Bonsor, A. & Gänsicke, B. T. Formation of planetary debris discs around white dwarfs—i. Tidal disruption of an extremely eccentric asteroid. Mon. Not. R. Astron. Soc. 445, 2244–2255 (2014).

    Google Scholar 

  82. Lynden-Bell, D. & Pringle, J. E. The evolution of viscous discs and the origin of the nebular variables. Mon. Not. R. Astron. Soc. 168, 603–637 (1974).

    Google Scholar 

  83. Goldreich, P. & Tremaine, S. The velocity dispersion in Saturn’s rings. Icarus 34, 227–239 (1978).

    Google Scholar 

  84. Esposito, L. W. Composition, structure, dynamics, and evolution of Saturn’s rings. Annu. Rev. Earth Planet. Sci. 38, 383–410 (2010).

    Google Scholar 

  85. Toomre, A. On the gravitational stability of a disk of stars. Astrophys. J. 139, 1217–1238 (1964).

    Google Scholar 

  86. Salo, H. Simulations of dense planetary rings III. Self-gravitating identical particles. Icarus 117, 287–312 (1995).

    Google Scholar 

  87. Daisaka, H. & Ida, S. Spatial structure and coherent motion in dense planetary rings induced by self-gravitational instability. Earth Planets Space 51, 1195–1213 (1999).

    Google Scholar 

  88. Salo, H., Schmidt, J. & Spahn, F. Viscous overstability in Saturn’s B ring: I. Direct simulations and measurement of transport coefficients. Icarus 153, 295–315 (2001).

    Google Scholar 

  89. Yasui, Y., Ohtsuki, K. & Daisaka, H. Viscosity in planetary rings with spinning self-gravitating particles. Astron. J. 143, 110 (2012).

    Google Scholar 

  90. Shukhman, I. G. Collisional dynamics of particles in Saturn’s rings. Sov. Astron. 28, 574–585 (1984).

    Google Scholar 

  91. Shu, F. H. & Stewart, G. R. The collisional dynamics of particulate disks. Icarus 62, 360–383 (1985).

    Google Scholar 

  92. Morishima, R. & Salo, H. Simulations of dense planetary rings: IV. Spinning self-gravitating particles with size distribution. Icarus 181, 272–291 (2006).

    Google Scholar 

  93. Salmon, J., Charnoz, S., Crida, A. & Brahic, A. Long-term and large-scale viscous evolution of dense planetary rings. Icarus 209, 771–785 (2010).

    Google Scholar 

  94. Dougherty, M., Esposito, L. & Krimigis, S. Saturn from Cassini–Huygens (Springer Science and Business Media, 2009).

    Google Scholar 

  95. Hedman, M. M. & Nicholson, P. D. Kronoseismology: Using density waves in Saturn’s C ring to probe the planet’s interior. Astron. J. 146, 12 (2013).

    Google Scholar 

  96. Hahn, J. M. & Spitale, J. N. An n-body integrator for gravitating planetary rings, and the outer edge of Saturn’s B ring. Astrophys. J. 772, 122 (2013).

    Google Scholar 

  97. Nicholson, P. D., French, R. G., Hedman, M. M., Marouf, E. A. & Colwell, J. E. Noncircular features in Saturn’s rings I: The edge of the B ring. Icarus 227, 152–175 (2014).

    Google Scholar 

  98. Beech, M. Electrophonic sound generation by the Chelyabinsk fireball. Earth Moon Planets 113, 33–41 (2014).

    Google Scholar 

  99. Pollack, J. B. & Burns, J. A. An origin by capture for the Martian satellites? Bull. Am. Astron. Soc. 9, 518 (1977).

    Google Scholar 

  100. Peale, S. J. & Canup, R. M. Treatise on Geophysics 2nd edn, 559–604 (Elsevier, 2015).

    Google Scholar 

  101. Schultz, P. H. & Lutz-Garihan, A. B. Grazing impacts on Mars: A record of lost satellites. J. Geophys. Res. 87, A84–A96 (1982).

    Google Scholar 

  102. Robbins, S. J. & Hynek, B. M. A new global database of Mars impact craters ≤ 1 km: 1. Database creation, properties, and parameters. J. Geophys. Res. 117, E06001 (2012).

    Google Scholar 

Download references

Acknowledgements

B.A.B. thanks the Open Earth Systems project funded by National Science Foundation grant EAR-1135382. K. Ferrier, B. Marsh, H. Lenferink, B. Buffett, R. Citron and M. Manga provided valuable feedback on earlier versions of this work. The authors gratefully acknowledge the support of M. Manga.

Author information

Authors and Affiliations

  1. Department of Earth and Planetary Science, University of California, Berkeley, Berkeley, California 94720, USA

    Benjamin A. Black & Tushar Mittal

  2. Department of Earth and Atmospheric Science, The City College of New York, City University of New York, 160 Convent Avenue, New York City, New York 10031, USA

    Benjamin A. Black

Authors
  1. Benjamin A. Black
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tushar Mittal
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

B.A.B. and T.M. jointly planned the research, performed the calculations, and wrote and revised the manuscript.

Corresponding authors

Correspondence to Benjamin A. Black or Tushar Mittal.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 475 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Black, B., Mittal, T. The demise of Phobos and development of a Martian ring system. Nature Geosci 8, 913–917 (2015). https://doi.org/10.1038/ngeo2583

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/ngeo2583

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing