Introduction

In spite of significant theoretical1,2 and experimental3,4 advances since the pioneering work of Adam and Gibbs5, it is as yet unclear whether the glass transition is thermodynamic or dynamic in nature. This is predominantly because supercooled liquids fall out of equilibrium well before the putative phase transition, be it dynamic or thermodynamic, is reached. This limitation has spurred the search for alternate ways of approaching the glass transition6,7,8, of which random pinning has attracted widespread interest in the last 2 years. Random pinning has mainly been studied within the framework of the Random First-Order Transition (RFOT) theory9,10, which predicts a thermodynamic ‘ideal’ glass transition at a finite fraction of pinned particles, for temperatures above the Kauzmann temperature of the unconstrained liquid7. By comparison, the contrasting perspective offered by the Dynamical Facilitation (DF) theory6,11 has received far less attention. Recently, it was shown that kinetically constrained spin models12, which form the conceptual basis of the DF theory, do not exhibit a thermodynamic phase transition with random pinning13. Nonetheless, a systematic analysis of facilitation in real glass-formers with random pinning is yet to be undertaken, and is imperative in order to gain a deeper understanding of the glass transition.

The DF theory postulates that structural relaxation is dictated by the concerted motion of localized mobile defects, termed excitations, and the slowdown of dynamics is attributed to a reduction in the concentration of these excitations. Here, we investigate these postulates experimentally, by performing optical video microscopy on dense binary hard-sphere like colloidal suspensions. From the analysis of particle trajectories, we identify and characterize excitations and find that they are localized in space and time. Further, we observe that the concentration of these excitations indeed decreases on approaching the glass transition. Moreover, by computing facilitation volumes and mobility transfer functions, we demonstrate that DF grows on approaching the glass transition. We also show that string-like cooperative motion emerges from the correlated dynamics of excitations. Most importantly, by using holographic optical tweezers to pin a subset of particles, we show that DF plays a significant role in governing structural relaxation, even when the glass transition is approached by increasing the concentration of pinned particles.

Results

Excitations are localized in space and time

We first investigated DF for the unpinned case, in a binary colloidal glass-forming liquid composed of silica particles (see the section ‘Experimental Details’ in Methods). To identify excitations, we employed the protocol developed in ref. 14. A particle was said to be associated with an excitation of size a and ‘instanton’ time Δt, if it underwent a displacement of magnitude a over a time interval Δt, and persisted in its initial and final positions for at least Δt. In practice, excitations were identified by defining for the coarse-grained trajectory of every particle i, the functional

Here, θ(x) is the Heaviside step function and ta, known as the commitment time, is typically chosen to be approximately three or four times the mean value of Δt for an excitation of size a (see the section ‘Identifying Excitations’ in Methods. Also see inset to Fig. 1a). To obtain sufficient statistics, we restricted our analysis to a=0.5σS. We observe that the distributions of instanton times Pa(Δt) for different area fractions ϕ nearly collapse onto the same curve and the mean instanton time ‹Δt› remains almost constant (Fig. 1a). Also, at large ϕ, ‹Δt› is much smaller than the structural relaxation time (Supplementary Fig. 1), which clearly shows that excitations are localized in time, in accordance with ref. 14.

Figure 1: Dynamical facilitation in the absence of pinning.
figure 1

a) Distribution of instanton times Pa(Δt) for ϕ=0.73 (open red circles), ϕ=0.74 (filled blue triangles), ϕ=0.75 (filled black inverted triangles), ϕ=0.77 (open brown squares) and ϕ=0.79 (open green diamonds), showing that excitations are localized in time. (Inset to a) Representative sub-trajectory of a particle coarse-grained over 2 s, shown in black, and the corresponding functional hi(t, ta; a) shown in red. The instanton time duration Δt and the commitment time ta are marked by dotted lines. The displacement is measured in units of a=0.5σS and the trajectory has been shifted arbitrarily along the y axis to make the rise in displacement coincide with region of non-zero hi(t, ta; a). (b) The function F(r; a) normalized by its value at r=σL for ϕ=0.74 (filled blue triangles), ϕ=0.75 (filled black inverted triangles), ϕ=0.77 (open brown squares) and ϕ=0.79 (open green diamonds), showing that excitations are localized in space. (c–e) Displacement field of particles for ϕ=0.73 (c), ϕ=0.75, (d) and ϕ=0.79 (e). The colourbar corresponds to particle displacements normalized by the excitation size a. Particles coloured in maroon indicate displacements ≥a. (f) Concentration of excitations ca vs ϕ. (g) Facilitation volume for various ϕs. The symbols and colours in g are same as those in a, b.

Full size image

To measure the spatial extent of excitations, we first computed the function

For t=−ta/2 and t′=ta/2, μ(r, t, t′; a) yields the displacement density at a distance r from an excitation of size a located at the origin at time t=0, over a time interval ta centred on 0. From μ(r, t, t′; a), the spatial extent of excitations was then extracted by defining the function

where g(r) is the radial pair-correlation function and decays within 8 particle diameters irrespective of ϕ (Fig. 1b), confirming that excitations are spatially localized objects that do not grow on approaching the glass transition14.

Evidence for growing DF

A visual indicator of the concentration of excitations ca is the particles’ displacement field computed over ‹Δt›=12 s (Fig. 1c–e). The decreasing fraction of particles with displacements greater than a (maroon spheres) observed in Fig. 1c–e strongly indicates a lowering in ca with increasing ϕ. More quantitatively, the concentration of excitations, formally defined as

where V is the volume and N is the total number of particles, indeed decreases with ϕ, in accordance with the DF theory (Fig. 1f).

The second major ingredient of the DF theory is facilitation, which assumes that new excitations primarily occur in the vicinity of existing excitations. To quantify the degree of facilitation in our system, we computed the facilitation volume

We observe that for all ϕs considered, vF(t) initially increases with time, reaches a maximum value at time tmax and then decreases at longer times (Fig. 1g). Moreover, both tmax and increase with ϕ (Fig. 1g), in complete agreement with recent simulations of atomistic glass-formers14 as well as spin models15.

Although the presence of facilitated dynamics has been observed in numerical simulations14,16,17,18 and experiments on driven granular media19,20, its relative importance as a mechanism of structural relaxation is still debated. Some studies claim that facilitation becomes increasingly important on approaching the glass transition14,17,18 whereas others maintain that its relevance diminishes20. Within RFOT, facilitation is a by-product of slow dynamics rather than its chief cause21. To examine the importance of DF in our system, we computed the mobility transfer function as defined in ref. 17 (see the section ‘Mobility transfer function’ in Methods for a definition of . 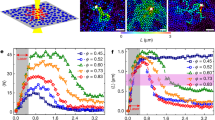We observe that analogous to ref. 17, for various ϕ, computed separately for large and small silica particles, exhibits a maximum at a time comparable to the cage-breaking time (Fig. 2a,b). Mmax is expected to increase over the regime in which facilitation is dominant, and decrease in the regime where other delocalized activated processes dictate relaxation15. We find that for 0.73≤ϕ<0.79, Mmax increases systematically, showing that DF plays an important role over this range of ϕ (Fig. 2c). Interestingly, at ϕ=0.79, Mmax shows a decrease relative to its value at ϕ=0.77 (Fig. 2c). We note that the typical distance travelled by most mobile particles over the cage-breaking time is ~0.5σs, which corresponds to the size a of the excitations considered in this work. For ϕ=0.79, the mean separation between these excitations, la=(taca)−1/2 (~40 μm), is comparable to the system size (~49 μm), whereas for all other ϕs, it is much smaller (<13 μm). The observed decrease in Mmax at ϕ=0.79 may therefore be a consequence of finite size effects15, although similar behaviour can stem from other delocalized activated relaxation processes. Nonetheless, the fact that Mmax remains significantly larger than 1, together with the substantial growth in facilitation volume shows that DF significantly contributes to structural relaxation over the range of ϕ considered in this work (see Supplementary Movie 1 for a visualization of facilitated dynamics).

Figure 2: Mobility transfer function (a,b).
figure 2

The mobility transfer function for small (a) and large (b) silica particles for ϕ=0.73 (open red circles), ϕ=0.74 (filled blue triangles), ϕ=0.75 (filled black inverted triangles), ϕ=0.77 (open brown squares) and ϕ=0.79 (open green diamonds). (c) Maximum of , Mmax, as a function of ϕ for small (open blue triangles) and large (filled black spheres) particles.

Full size image

Correspondence between excitations and microstrings

Consistent with RFOT and the Adam-Gibbs theory, a considerable body of evidence supporting the existence of growing dynamic length scales on approaching the glass transition22,23,24,25,26 has accumulated over the last two decades. It is natural to wonder if these growing dynamic correlations are influenced by DF. To investigate this possibility, we explored the connection between localized excitations and string-like cooperative motion of mobile particles24,27,28, which is believed to be consistent with RFOT29,30. We constructed strings from the top 10% most mobile particles using the procedure described in ref. 24. Figure 3a shows a representative string composed of 13 particles for ϕ=0.79, for which , where t* corresponds to the maximum of the non-Gaussian parameter α2(t) (ref. 22). From their trajectories over t*, the particles constituting the string can be divided into three independent groups, termed ‘microstrings’31, such that motion within each microstring is coherent (Fig. 3b–d). We observe that in one of the microstrings (Fig. 3d), each particle i is associated with an excitation for some time Δti<t* (Fig. 3e), which strongly suggests that over t*, the motion in the other microstrings is facilitated by these excitations. Moreover, the maximum string length increases with the mean separation between excitations (Supplementary Fig. 2). Collectively, these findings show that string-like cooperative motion at longer times emerges in a hierarchical manner, from the short-time dynamics of excitations14.

Figure 3: Connection between excitation dynamics and microstrings.
figure 3

(a) Schematic of a representative string composed of 13 particles for ϕ=0.79 constructed over a time interval . Particles in yellow, red and blue correspond to initial positions of particles belonging to three independent microstrings. Cyan spheres represent final positions of the particles. (b–d) Trajectories of particles corresponding to the blue (b), red (c) and yellow (d) microstrings over time t*. In b–d, the particle labels are identical to those in a. (e) The functional hi(t, ta; a), where a=0.3σS, corresponding to the trajectories shown in d for the yellow microstring in a.

Full size image

Evolution of facilitation with random pinning

In the presence of random pinning, numerical evidence based on static quantities supports the RFOT scenario32, whereas that based on dynamic ones does not33. However, the rapid growth of relaxation times with increasing fraction of pinned particles is undisputed7,32,33. It is thus natural to ask whether DF accounts for the observed slowdown of dynamics. Indeed, as the DF theory is a parallel approach to RFOT, a systematic investigation of facilitation in the context of random pinning is highly desirable7 and is likely to enrich our understanding of the glass transition. We therefore explored the impact of DF on structural relaxation in the presence of random pinning. Towards this end, we imaged a binary mixture of polystyrene particles at fixed ϕ, and used holographic optical tweezers to pin a subset of particles in the field of view (Fig. 4a. Also see the sections ‘Experimental details’ and ‘Estimation of the trap potential’ in Methods. See Supplementary Movie 2 for a visualization of glasst dynamics in the presence of pinned particles). The fraction of pinned particles fp was varied from 0.03 to 0.26. We see that even at relatively low values of ϕ and fp, the pinned particles have a significant impact on the dynamics of the remaining free particles. The structural relaxation time increases by a factor of 4 relative to its value in the unpinned case (Fig. 4b) for ϕ=0.71 when fp is varied from 0.03 to 0.12. Further experiments at higher values of ϕ and fp reveal that in concord with recent simulations32,33, the slowdown in dynamics with pinning becomes increasingly pronounced at larger ϕs (Fig. 4b). Most importantly, at ϕ≥0.74 and fp ≥0.21, the system becomes non-ergodic over experimental time scales, as evident from the profile of the self-intermediate scattering function Fs(q0, t) (Supplementary Fig. 3. Also see Supplementary Movie 3 for a visualization of the slowdown of dynamics with fp). These results indicate the possible existence of a glass transition induced by random pinning. To verify whether the observed increase in with fp is a consequence of growing facilitation, we repeated the analysis shown in Fig. 1 for the pinned case. At ϕ=0.71, we observe that the concentration of excitations ca decreases by more than a factor of 3 with fp (Fig. 4c), whereas the facilitation volume shows a concomitant increase (Fig. 4d), for fp ranging from 0.03 to 0.12. We observe a similar evolution of ca (Fig. 4c) and (Supplementary Fig. 4) with fp for higher ϕs as well. These results show that in striking resemblance to the unpinned case (Fig. 1f,g), DF plays a significant role even in the context of the random pinning glass transition.

Figure 4: Effect of random pinning.
figure 4

(a) Schematic of the trapping potentials (shown in red) created by the holographic optical tweezers. The underlying image represents a small portion of the field of view for fp=0.06 and ϕ=0.71. The image has been generated by averaging over . Pinned particles appear bright because of their low mobility and high overlap with initial positions. (b) Structural relaxation time for free particles as a function of fp for ϕ=0.71 (filled black spheres) and ϕ=0.74 (filled red triangles). Note the break in the axis. (c) Concentration of excitations ca as a function of fp for ϕ=0.71 (filled black spheres) and ϕ=0.74 (filled red triangles). In b and c, only those data points for which Fs(q0,t) decays at least to 1/e are shown. (d) Facilitation volume vF(t) for fp=0 (open black squares), fp=0.03 (open red circles), fp=0.06 (open blue triangles) and fp=0.12 (open green inverted triangles). (e) Distribution of string lengths P(n) for corresponding to the maximum string length and (f) string length for various fp. In d–f, ϕ=0.71. The colours and symbols in e and f are identical to those in d.

Full size image

Next, we examined the interplay between facilitation and string-like cooperative motion in the presence of random pinning. We observe that the behaviour of string-like cooperative motion as a function of fp is remarkably similar to its variation with ϕ. In particular, the distribution of string lengths P(n) is nearly exponential (Fig. 4e), and the average string length ns=Σn2P(n)/ΣnP(n) exhibits a maximum as a function of time (Fig. 4f. See Supplementary Fig. 2 for corresponding results in the unpinned case). Further, the time at which ns reaches a maximum, , increase systematically with fp (Fig. 4f). However, in contrast to the unpinned case, the maximal string length does not grow systematically with increasing fp (Fig. 4f and Supplementary Fig. 4). Interestingly, the four-point dynamic susceptibility χ4(ap, t) (see the section ‘Dynamic susceptibility’ in Methods for a definition) does not exhibit a systematic increase with fp (Supplementary Fig. 5), which is consistent with ref. 33 as well as the dependence of string lengths on fp (Fig. 4f). Although DF in known to result in the growth of χ4(ap, t) on approaching the glass transition in the absence of pinning1, a correspondence between facilitation and χ4(ap, t) in the context randomly pinned particulate systems is yet to be established. Our findings therefore warrant investigation in future experiments and simulations.

Discussion

Our experiments have highlighted the importance of DF on approaching the colloidal glass transition, be it driven by density or random pinning. Although the procedure to characterize excitations employed here involves the analysis of particle displacements, it has been speculated15 that localized soft modes16 may provide a method of identifying excitations, without recourse to their dynamics. This is a very interesting possibility that needs to be investigated experimentally as well as numerically. Yet another promising avenue is the development of amorphous order on approaching the glass transition. Although the DF theory makes no predictions for structural evolution on approaching the glass transition, signatures of growing amorphous order in the form of overlap functions32,34 and point-to-set correlations35,36 have been observed in numerical simulations. It is of paramount importance to examine whether DF can be reconciled with the growth of these static correlations. In particular, it would be worthwhile to probe whether facilitation plays a role in the generic decoupling of static and dynamic length scales26,37. Finally, we expect our observations to stimulate theoretical and numerical research on dynamic space-time phase transitions between mobile liquid and immobile glassy states6,38 in the presence of random pinning. Specifically, as ca is known to be an order parameter for such space-time phase transitions39, the observed decrease in ca with fp (Fig. 4c) implies that changing fp influences the system’s proximity to a dynamic phase transition. It would be fascinating to examine whether or not this dynamic phase transition coincides with the thermodynamic one predicted by RFOT7. We expect a confluence of experimental, theoretical and numerical research aimed at exploring these questions to emerge in the wake of our findings.

Methods

Experimental details

For experiments without pinning, the system comprised of NL large and NS small silica colloids of diameters σL=970 nm and σS=760 nm, respectively. The size ratio σL/σS=1.3 and the number ratio NL/NS=0.66 effectively suppressed crystallization. Dilute samples were loaded in a wedge-shaped cell40 and the area fraction ϕ was tuned systematically by controlled sedimentation of particles to the monolayer thick region of the wedge. For experiments with pinning, we used a binary mixture of polystyrene spheres of diameters 1.4 and 1.05 μm. For ϕ=0.71, the number ratio NL/NS was 2.3, whereas for experiments at larger ϕ, this ratio was reduced to 0.7 in order to enhance the frustration to crystallization. Both silica and polystyrene particles interact via short-ranged repulsive screened Coulomb interactions with a Debye length that is typically smaller than 10% of the particle diameter. To a good approximation, therefore, these systems can be treated as suspensions of effective hard spheres. The holographic optical tweezers set up consisted of a linearly polarized constant power (800 mW) CW laser (Spectra-Physics, λ=1,064 nm). A spatial light modulator (Boulder Nonlinear Systems, Inc.) was used to generate upto 200 traps at randomly chosen locations. Only large polystyrene particles were pinned. The laser was switched on after fixing the trap positions and equilibrating the sample to ensure simultaneous activation of the traps. The average power per trap (~0.5 mW) was sufficient to ensure that the pinned particles did not escape over the duration of the experiment, as evidenced by the difference in mean squared displacements of free and pinned particles (Supplementary Fig. 6). For experiments with and without pinning, samples were imaged using a Leica DMI 6000B optical microscope with a × 100 objective (Plan apochromat, numerical aperture=1.4, oil immersion) and images were captured at frame rates ranging from 2.5 to 5 f.p.s. for 1–3 h depending on the values of ϕ and fp. The 66 × 49 μm2 field of view typically contained >4,000 particles for the silica sample and ~1,200 particles for the polystyrene sample. For experiments in which a maximum fp≥0.21 was reached, a restricted field of view of 34 × 37 μm2 containing ~600 polystyrene particles was used. Standard algorithms were used for particle tracking41 and quantities of interest were extracted using codes developed in-house.

Identifying excitations

As the functional hi(t, ta; a) does not impose an upper bound on the size of excitations, the algorithm detects excitations of size greater than a, if their Δt is sufficiently small. These anomalously large excitations were ignored, in order to ensure that they do not bias the analysis. To calculate hi(t, ta; a), the initial guess for Δt, Δtin, was chosen by manually inspecting a few trajectories, and the corresponding initial value of ta was set to be slightly larger than 3Δtin. From these initial guesses, we computed hi(t, ta; a) and plotted a distribution of Δt. The mode Δtm of this distribution was chosen as the initial value of Δt for the final computation of hi(t, ta; a), and ta was accordingly set to a value slightly greater than 3Δtm. The results are insensitive to the choice of Δt, but depend strongly on ta.

Mobility transfer function

Given two successive time intervals Δt1 and Δt2 of a fixed duration such that , the mobility transfer function quantifies the excess probability for a mobile particle in Δt2 to be located close to a mobile particle in Δt1, relative to the probability that it is located near an immobile particle. To compute , we identified the top 10% most mobile particles for two successive intervals of duration and generated the distribution of the minimum distance of each mobile particle in the second interval from the set of mobile particles in the first interval. Particles that are mobile over both intervals were not considered for the analysis. We also generated a reference distribution of the minimum distance of each mobile particle in the second interval from a set of randomly chosen immobile particles in the first interval. From these two distributions, we computed , formally defined as

where rmin corresponds to the first minimum of the radial pair correlation function g(r).

Estimation of the trap potential

For fp ≥0.21, where the mean separation between traps is of the order of 2σ, we ensured that the slowdown in dynamics was due to the presence of a trapped particle and not due to the potential of the trap. Towards this end, we computed the radial pair correlation function g(r) of a dilute suspension (ϕ=0.26) of the smaller polystyrene particles with respect to a large reference polystyrene particle that was stuck to the glass coverslip. We then compared this g(r) with the radial pair correlation of the same liquid in the presence of an optical trap centred on the stuck particle. We observed a slight enhancement in the first peak of g(r) because of the presence of the trap (Supplementary Fig. 7), indicating that the trap contributes a small attractive potential in addition to freezing the particle on which it is centred. Using the dilute limit approximation to the potential of mean force42, we obtained a crude estimate of this excess potential and found it to be ~0.15 kBT. Further, beyond r=1.1σ, the two correlation functions overlap, indicating that the potential of the trap decays well within the first nearest neighbour shell. This confirms that the glass transition seen in our experiments is purely an effect of the presence of pinned particles and is not influenced by the trap potential.

Dynamic susceptibility

To calculate the dynamic susceptibility χ4(ap, t)43, we first computed the self-overlap function

where N is the total number of particles. The probe length scale ap was varied from 0.03σ to σ, where σ corresponds to the first maximum of g(r). We then extracted χ4(ap, t) from the fluctuations in Qs(ap, t)

The angular brackets indicate ensemble as well as time averaging. For the data shown in Supplementary Fig. 5, the value of ap that maximized χ4(ap, t) was chosen as the probe length scale.

Additional Information

How to cite this article: Gokhale, S. et al. Growing dynamical facilitation on approaching the random pinning colloidal glass transition. Nat. Commun. 5:4685 doi: 10.1038/ncomms5685 (2014).