Abstract
One of the most questionable issues in wetting is the force balance that includes the vertical component of liquid surface tension. On soft solids, the vertical component leads to a microscopic protrusion of the contact line, that is, a ‘wetting ridge’. The wetting principle determining the tip geometry of the ridge is at the heart of the issues over the past half century. Here we reveal a universal wetting principle from the ridge tips directly visualized with high spatio-temporal resolution of X-ray microscopy. We find that the cusp of the ridge is bent with an asymmetric tip, whose geometry is invariant during ridge growth or by surface softness. This singular asymmetry is deduced by linking the macroscopic and microscopic contact angles to Young and Neuman laws, respectively. Our finding shows that this dual-scale approach would be contributable to a general framework in elastowetting, and give hints to issues in cell-substrate interaction and elasto-capillary problems.
Similar content being viewed by others
Introduction
Many natural and synthetic materials are soft and deformable owing to the nature as in rubbers or to their structure as for thin films1,2,3 and fibres4,5,6. Wetting behaviour of soft deformable solids, that is, elastowetting, is a very old subject and much attention has been paid over the past half century1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26 for various scientific issues involved in soft tissues27,28,29,30,31,32 and polymer gels33, as well as for practical applications such as inkjet printing34 and microfluidic devices35. Recently, the interaction of the contact line with a deformable substrate, which causes a local microscopic deformation, that is, the formation of a ‘wetting ridge’, has been actively investigated7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25 since the pioneering work on the first measurement of the ridge by Carré et al.20
Wetting behaviours on solids have been explained by Young law (cosθL=(γSV–γSL)/γLV)36, based on a force balance of interfacial tensions (γLV, γSV and γSL of liquid–vapour, solid–vapour and solid–liquid interfaces, respectively) that determines the equilibrium contact angles (θS, θL and θV in solid, liquid and vapour, respectively) at the three-phase contact line.
On a soft solid, however, the vertical component of liquid surface tension, which is not considered in Young law, has critical roles in the wetting behaviours, such as the wrinkling1,2 or folding3 of thin films and the bending of fibres4,5,6. The vertical component, which is highly concentrated at the microscopic region of the three-phase contact line, induces a local microscopic structure on the soft surface, that is, a ‘wetting ridge’. Despite many theoretical7,8,9,10,11,12,13,14,15,16 and experimental7,17,18,19,20,21,22,23,24,25 studies over the past half century, the microscopic geometry of a wetting ridge, particularly, its ‘tip geometry’, still remains unresolved.
The first measurement of the wetting ridge was achieved by using white-light interferometry, which was limited to the dry side of the ridge far from the tip20. Since then, many researchers have tried to find the tip using optical techniques such as confocal microscopy7,18,19 or optical profilometry21. However, direct observation of the tip for precise measurements of the contact angles is hardly achievable by optical imaging owing to limited resolutions7,18,19,20. For instance, confocal microscopy18 failed to directly visualize the vicinity of the contact line due to strong light scattering over the detection limit by the steep slopes near the contact line. Jerison et al.7 first measured triangular cusps by embedding fluorescence particles on the surface in confocal microscopy. The resolution of this approach, however, was not high enough to visualize the tip and precisely measure the geometry of the cusp. Here we present the first, direct and real-time visualization of ridge tips with high spatial and temporal resolutions using X-ray microscopy, and discuss a general framework of wetting on soft solids based on precise measurement of the geometry of the tips.
Results
Direct visualization of ridge tips
For this study, we used transmission X-ray microscopy (TXM), as illustrated in Fig. 1a, to provide direct visualization of a wetting ridge for a water (or 40% ethylene glycol aqua solution (EG 40%)) drop (r≈1 mm) on a silicone gel (or polydimethylsiloxane (PDMS)) surface (Fig. 1b). All of the three interfaces, particularly including the LV interface, at the tip of a wetting ridge were clearly visualized, as demonstrated in Fig. 1c, with a high spatial resolution (~50 nm per pixel) without using any contrast agents. The interference bright and dark fringes at each interface, originating from the Zernike phase contrast37,38, allowed us to clearly identify each interface39,40. We for the first time found that wetting ridges in large drops (r≈1 mm) have bent cusps (Fig. 1d; dashed square of Fig. 1c) with the asymmetric tips rotated (Fig. 1e; dashed square of Fig. 1d) towards the LV interfaces (Fig. 1d,e). The rotation of the tips observed here is different from the reported rotation of the whole ridges that is due to the substantial dimple generated under small droplets (r<<250 μm) by large Laplace pressures19. High-resolved images of the tips of cusps enabled us to accurately measure the microscopic (θS, θL and θV) as well as the macroscopic (θ) contact angles (Fig. 1e; dashed square of Fig. 1d).
(a,b) Schematic illustrations of (a) transmission X-ray microscopy (TXM) and (b) a sessile drop on a soft substrate. TXM consists of a capillary condenser, a motorized sample stage, a zone plate (ZP), a phase ring (PR) and a CCD camera. A wetting ridge (red square in b) is formed by the surface tension of a water drop at the contact line. (c,d) Demonstration of a directly visualized (c) wetting ridge with (d) a bent cusp (magnified image of the dashed square in c) and an asymmetric tip (dashed square in d). (e) Extraction of three interfaces from the ridge tip (magnified image of the dashed square in d), which enables us to measure the macroscopic (θ) and the microscopic (θS, θV and θL) contact angles. (c,d) Scale bars, 2 and 1 μm, respectively.
Surface profiles
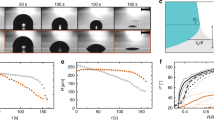
The direct visualization made it possible to accurately extract the surface profiles uz(x) (vertical surface displacement at x) of wetting ridges (Supplementary Fig. 1), as demonstrated for two surfaces with E (elasticity)=3 and 16 kPa in Fig. 2a,b. The two profiles (blue and red circles in Fig. 2b) clearly show asymmetric and bent cusps. Here the horizontal peak position of each surface profile was set as x=0. We tried to fit the following three linear elastic (LE) symmetrical models to these profiles (Supplementary Fig. 2): (i) the model by de Gennes and Shanahan10,11,20 (dash-dotted lines) based on the classical stress analysis of an elastic film by a concentrated normal force; (ii) the model by Limat12 (dashed lines) based on symmetric surface energies (γSV=γSL=γS, that is, θ=90°); and (iii) the model by Style and Dufresne7,8 (solid lines) based on symmetric surface stresses (ΥSL=ΥSV=ΥS), where ΥSL (ΥSV) is the surface stress of the SL (SV) interface. The best fits of the three models are displayed in Fig. 2b.
(a) Representative X-ray images of wetting ridges on a silicone gel (E≈3 kPa) and a PDMS film (≈16 kPa). Scale bars, 5 μm. (b) The surface profiles clearly show a strong E-dependence of the vertical displacement uz(x). The asymmetric and bent cusps are compared with three LE symmetrical models by Style et al.8 (solid lines), Limat12 (dashed lines) and de Gennes and Shanahan10,11,20 (dash-dotted lines). For E≈3 kPa, the model by Shanahan is invalid in the observed region here. The detailed fitting descriptions are in Supplementary Fig. 2. (Inset) The cusps are identically superimposed by Δuz(x)=uz(x)−uz(0) at w<<le. (c) (Top) The angular differences (ΔAngle) are plotted with E, based on the average values for 3 kPa, for the macroscopic (θ, black circle) and the microscopic (θS (blue circle), θV (blue square) and θL (blue triangle)) angles measured at w< ~0.4 μm. The error bars are s.d. from five sets of image data for 3 kPa, one set for 10 kPa and three sets for 16 kPa. (Bottom) K is obtained with θS and γLV, that is, K=sinθS/γLV. The little difference of K (ΔK<4%), resulted from that of ΔθS (< ±1.6°), indicates invariant surface stresses ΥSL and ΥSV at the tips.
The surface profiles predicted by most of LE symmetrical models7,8,9,10,11,12,13,14,15,20 are not well matched with our experimental data (Fig. 2b and Supplementary Fig. 2), except the model by Style and Dufresne8 in EG 40% (Supplementary Fig. 2f). In fact, the predicted profiles themselves are quite different from each other. The heights of ridges predicted ~γLVsinθ/E are relatively in a good agreement with those measured in this study uz(0), though (Table 1).
The model by Shanahan and co-workers10,11,20 is inapplicable to predict the profiles in the cusp regions (w (ridge width) << le (=ΥS/E, the elasto-capillary length)). Actually, the cusp regions are inelastic regions (|x−x′|≲ε, where x′ is the position of the contact line and ε is the cutoff distance10), based on the fact that the estimated ε are comparable to le for our systems (Table 1). Of course, the model is relatively well matched in the elastic zone (|x−x′|≳ε) the dash-dotted line (the green solid line) in |x|>~5 μm in Fig. 2b (Supplementary Fig. 2a), consistent with Fig. 2 of ref. 20.
The surface profiles by Limat12, who included symmetric surface energies (γSV=γSL=γS) in the Shanahan’s description of surface displacement10,11,20, are furthermore far from our experimental data (Supplementary Fig. 2c,d; the solid lines are from surface energies, γS=(γSV+γSL)/2 and the dashed lines are from surface stresses, ΥS=(ΥSV+ΥSL)/2). The deviation is presumably due to oversimplification, in particular, by the assumptions of θSV(SL) <<1 and γLV <<γS, which are in contrast to our case (θSV >>1 and γLV (ΥLV)>γS (ΥS)), where θSV(SL) is the slope of the SV (SL) interface.
The best fits were obtained by using the model by Style and Dufresne8 (Fig. 2b and Supplementary Fig. 2e,f) that accounts for the surface tension of solid, that is, the surface stress. For the water system with asymmetric surface energies (γSV≠γSL), the surface profiles are relatively in a good agreement with our data in the region of w>>le, but not in the region of w<<le, where the cusp shows significant asymmetry (Fig. 2b and Supplementary Fig. 2e). For the EG 40% system with symmetric surface energies (γSV≈γSL), the profiles (in particular, the green solid line) in Supplementary Fig. 2f correspond to the experimental data in overall region. However, this symmetrical model intrinsically fails to capture the microscopic contact angles at ridge tips that are actually asymmetric even in symmetrical surface energies.
The profiles, especially, in the region where w<<le, are significantly deviated from the best fits of the three models, presumably due to large asymmetry and/or large strain at the tips. In calculating uz(x) in Fig. 2b, we assumed ΥS=(ΥSL+ΥSV)/2 or γS=(γSV+γSL)/2, where ΥSL (ΥSV) was measured from our experimental data and γSV (γSL) was extracted from literatures41,42. Over the region where w>>le, however, the model by Style and Dufresne8 is better matched to our experimental data than the other models10,11,12,20. We note that in any systems with γSV≈γSL (that is, θ≈90°) or a small γLV, the ridge profiles can be approximately symmetric, except their tips (Supplementary Fig. 2f). In fact, Style and Dufresne7,19 observed symmetric triangular cusps in the large drop limit (r>>250 μm), which were very close to their model despite the simple approximation. However, their approach is in principle not correct as it neglects any source of asymmetry, in particular, the difference between ΥSL and ΥSV. The accurate observation of the tip geometry has been unattainable so far.
Solid elasticity
More interestingly, we found that the shapes of two cusps in our experimental data are nearly identical or self-similar (the inset of Fig. 2b), regardless of E or the ridge height uz(0) (~γLVsinθ /E)7,8,10,12,14,20, which is consistent with other references7,8,19 except the asymmetry. To confirm the self-similarity, we measured the macroscopic and the microscopic contact angles (Fig. 1e) in a length of ~0.4 μm for various surface elasticities, as listed in Supplementary Table 1, and the angular dependencies on surface elasticity were plotted in Fig. 2c (top) based on the averaged values for E≈3 kPa. Interestingly, we found that the variation of each angle by elasticity is very small despite the strong elasticity dependence of uz(x). In particular, the small difference in ΔθS (< ±1.6°) leads to a nearly constant K (=sinθS/γLV) with E as in Fig. 2c (bottom, ΔK <4%), directly indicating that the two surface stresses of ΥSL and ΥSV are invariant with E, as deduced from Neuman relation (K=sinθS/γLV=sinθV/ΥSL=sinθL/ΥSV)19. Herein, surface stresses43 (specifically, ΥSV and ΥSL), instead of surface energies (γSV and γSL), are applied as effective interfacial tensions for SV and SL interfaces19, which also helps to overcome a paradox: a force balance at the tip but the violation of the Neumann triangle condition in terms of the surface energies as γW(or EG 40%)>γPDMS+γW(or EG 40%)–PDMS (Table 2). Here, we note that θS is in good agreement with the calculated value from the asymmetric case of Limat’s model12 (Supplementary Table 2 and Supplementary Note 1), which indicates that asymmetry of surface stresses or surface energies is undoubtedly a critical factor determining the ridge tip geometry.
A rather large deviation in the macroscopic angle (θ) presumably results from the evaporation of the water drops and the heterogeneity of the soft surfaces. We found that the macroscopic angle (θ=108.1±9.0°) for the soft surfaces is consistent to that (θ=106.6±2.3°) for rigid surfaces (E≈750 kPa; see Methods section). This suggests that Young law would hold regardless of E. We note that herein Young law is valid in terms of surface energies in macroscopic scale (drop size: approximately millimetre), where the contribution of the local deformation (approximately micrometre) at the contact line to the surface stresses is negligible. Here the effect of the Laplace pressure is negligible for large droplets (r>>250 μm) as in our case (r≈1 mm; Table 1 and Supplementary Note 1), different from the large Laplace pressure for small droplets (r<<250 μm) that causes significant rotation of the ridge and decrease of the ridge height by making a large dimple under the droplets19.
Ridge-growth dynamics
To explore wetting dynamics on soft solids, ridge-growth dynamics should be first studied but is rarely known with few observations22,23. We used non-volatile EG 40% drops, instead of evaporating water drops, during dynamic experiment. High temporal resolution of TXM enabled us to take real-time movies of ridges during their growth. Figure 3a demonstrates a ridge growth for a EG 40% drop on silicone gel (E≈3 kPa), recorded 1–2 min after contact line pinning until the contact line is depinned by injecting EG 40% into the drop (Supplementary Movie 1). We plotted both the ridge height uz(0) and the change of the solid contact angle ΔθS (within w< ~0.7 μm) as a function of observing time in Fig. 3b. We find that uz(0) linearly increases at a rate of~7 nm s−1. Here the abrupt decrease in uz(0) at 181 s (red arrows in Fig. 3a,b) is due to the depinning. Very interestingly, the contact angles (θS) at all the ridge tips observed were nearly invariant despite their gradual increase in uz(0), as demonstrated in Fig. 3b.
(a) Representative sequential snapshots of a cusp during ridge growth for a EG 40% drop on a silicone gel (E≈3 kPa and h≈50 μm; Supplementary Movie 1). The cusp was instantly recovered (red arrow) right after depinning at 181 s (grey dotted line). Scale bar, 2 μm. (b) (Top) The ridge height uz(0) increases at a constant rate of ~7 nm s−1 until depinning at Δt (observing time)=181 s. The abrupt decrease right after depinning (red arrow) is attributed to an instantaneous elastic recovery. (Bottom) ΔθS is unchanged during the ridge growth (θS=56.3±5.1°). X-shaped symbols in b is the values obtained after depinning. Black dashed lines are a guide to the eye. (c) A schematic illustration of ridge growth from t=t1 to t=t3. Invariant θS during the slow and linear ridge growth in b might be caused by a liquid-like viscous flow in the soft substrate.
Discussion
Geometric invariance in the tip (w<<le) during ridge growth or by surface softness indicates that cusp formation is controlled by capillarity and not by elasticity7,8. For a large drop with a negligible line tension and a negligible Laplace pressure, only three interfacial tensions can affect ridge formation. Herein, we exclude the possible existence of an extra tangential force by the long-range interaction between liquid and solid molecules suggested in refs 13, 14, as discussed in detail in Supplementary Fig. 3, Supplementary Table 3 and Supplementary Note 1. We illustrated the force balances at the ridge tips for water and EG 40% drops in Fig. 4. Here we see that the measured surface stresses are asymmetric (ΥSV≠ΥSL), regardless of whether γSV≈γSL or θ≈90° (Fig. 4). This results in the formation of the asymmetric tips (θV≠θL). The difference in the surface stresses is because of their dependence on the mediums surrounding the surfaces44. The surface stresses can be also affected by surface elastic deformation that depends on the vertical component of the liquid surface tension. This explains the different surface stresses (ΥSV(W)>ΥSV(EG 40%)) in the two systems with different surface tensions (γW>γEG 40%) (Table 2). The precise measurement of the cusp geometry by our approach enabled us to find the asymmetric cusp geometries and thus to obtain the surface stresses accurately. The SV surface stress ΥSV was measured as 59 (42) mN m−1 in a water (EG 40%) drop on silicone gel using our approach, which is larger than that (31 (28) mN m−1 in a glycerol (fluorinated oil) drop on silicone gel) measured by confocal microscopy19.
The bending of the cusp, clearly depicted in Fig. 4a, is attributed to the inclination of the LV interface with θ>90°, which is due to the asymmetric surface energies (γSV≠γSL). It is conceivable that by Neuman law the microscopic angles of the tip are established with respect to the inclined LV interface, leading to the rotation of the tip and thus the bending of the cusp (w<<le). These results suggest that the geometry of the cusp with the rotated tip is determined by simultaneously applying macroscopic and microscopic force balances by Young and Neuman laws, respectively, as suggested by Style et al.8 More importantly, our results show applicability of such a dual-scale approach to a general framework of wetting on soft solids within a wide softness range and with asymmetric surface energies/stresses.
The time-invariant tip geometry (Fig. 3), which indicates time-invariant surface stresses, suggests that the ridge growth observed would be due to an inelastic deformation43. Specifically, the slow and linear growth of the ridges with the invariant contact angles (θS) suggests that the ridge growth is, as illustrated in Fig. 3c, caused by a viscous flow in the soft solid, similar to that in a very viscous liquid22. Viscoelastic deformation of the ridge has been also observed even on elastomers, as reported by some irreversible part of the ridge growth for long residual times (approximately a few min) of a drop24. Further study is required to correlate the ridge growth and the plastic deformation.
In conclusion, we present the first direct visualization of wetting ridge tips on soft solids using high-resolution TXM. We revealed that the tip geometry of the wetting ridges has asymmetry and the cusps are bent by the inclined LV interfaces. From the measurements of the microscopic and macroscopic contact angles at their tips, we found that the microscopic geometry of the tip is invariant during the ridge growth or by the surface elasticity. The singular geometry of the cusps can be deduced by simultaneously applying Young and Neuman laws for macroscopic and microscopic force balances, respectively, as suggested by Style el al.8, but with using asymmetry of surface energies and surface stresses in our case. Our results show that the dual-scale approach would be applicable to general wetting behaviours on soft solids, beyond the limit of a linear elasticity or the assumption of symmetric surface energies/stresses7,8,10,11,12,20. Furthermore, our approach is a general technique that can be used to measure accurate surface stresses for soft materials within a wide stiffness range. This report would open a new subject in wetting on soft solids, especially regarding study on asymmetric ridge tip. Broadly speaking, X-ray microscopy would be helpful to investigate characteristic wetting behaviours on soft solids associated with spreading20,21,22, contact angle hysteresis23,24,25 or evaporation23,25, and to study various elasto-capillary phenomena26.
In this report, we suggest an applicability of a simple approach applying both Young and Neuman laws to dual-scale force balance and continuous surface deformation, which would be potentially important, particularly, in biological systems. For example, cell–substrate interactions might be closely linked to wetting behaviours on soft solids17; in fact, cells are known to sense and respond to the environment through small strains (3–4%) that are induced by their traction forces28. Indeed, the mechanical microenvironment is, as seen in cancer progression in breast epithelial cells30, critical to the normal development of most mammalian tissues and organs, which are soft viscoelastic materials (E=10−1 (for example, a brain) to 102 kPa (for example, a cartilage))27. In addition, our approach might be practically applicable to estimating the cell traction force or the force-induced strain29, as well as the surface stresses19.
Methods
Materials and substrate fabrication
Pure water (Millipore) or EG 40% (Samchun Pure Chemical Co., Korea) drops of r≈1 mm were generated by a syringe pump and gently put on a silicone gel (E≈3 kPa; CY52-276A/B, Dow Corning Toray) or a PDMS (E≈10 or 16 kPa; Sylgard 184, Dow Corning Toray), spin coated with a controlled thickness (h=50 μm) on a Si wafer (Fig. 1b). Detailed protocols of preparing the substrates and their mechanical/rheological properties have been reported in refs 7, 19, 45, 46, 47. Si wafer as a solid support was used for the fine alignment of the samples to the X-ray beam, as confirmed by a mirror image of a wetting ridge (Fig. 2a) below the critical angle (0.22°) of Si.
X-ray imaging
The experiment was conducted using TXM (Fig. 1a)37,38 at the 32-ID-C beamline in the Advanced Photon Source of the Argonne National Laboratory. We used a focused monochromatic X-ray beam at the photon energy of 9 keV (depth of focus: ~25 μm). The high brightness yielded high spatial resolution (50 nm per pixel) in a short acquisition time (50 ms per frame), much faster than reported48,49,50,51. A Fresnel zone plate was used as an objective lens. For phase-contrast enhancement, we used a Au Zernike phase ring, optimized for 9 keV, which is very useful to imaging soft matters such as organic39,40 or biological samples37,38 without any contrast agents. Image taking was started within 1–2 min after contact line pinning, under controlled temperature (22.5 °C) and humidity (19.5%).
Data analysis
The contact angle θ for a rigid PDMS (E≈750 kPa) was, measured for five drops of water or EG 40% using optical microscopy, 106.6±2.3° or 95.8±0.7°, respectively. To test Young and Neuman conditions, we used the surface or interfacial tension of a liquid drop (PDMS oil or water (EG 40%)/PDMS oil) measured in the literatures41,42 (Table 2). Surface tension is the same as surface energy in liquid. Effects of X-ray irradiation52 to interfacial tensions or surface stresses are negligible, as confirmed by invariant contact angles. The surface profiles were extracted from the images using MATLAB and Image Pro-Plus 6.0 software (Supplementary Fig. 1)51,52. We calculated the surface profiles of the LE symmetrical models using MATLAB with the code for the model by Style et al.8 ( http://www.eng.yale.edu/softmatter/pubs.html). The surface profiles, calculated for different elastic moduli, were plotted in Supplementary Fig. 2.
Additional information
How to cite this article: Park, S. J. et al. Visualization of asymmetric wetting ridges on soft solids with X-ray microscopy. Nat. Commun. 5:4369 doi: 10.1038/ncomms5369 (2014).
References
Huang, J. et al. Capillary wrinkling of floating thin polymer films. Science 317, 650–653 (2007).
Huang, J., Davidovitch, B., Santangelo, C. D., Russell, T. P. & Menon, N. Smooth cascade of wrinkles at the edge of a floating elastic film. Phys. Rev. Lett. 105, 038302 (2010).
Py, C. et al. Capillary prigami: spontaneous wrapping of a droplet with an elastic sheet. Phys. Rev. Lett. 98, 156103 (2007).
Bico, J., Roman, B., Moulin, L. & Boudaoud, A. Elastocapillary coalescence ion wet hair. Nature 432, 690 (2004).
Duprat, C., Protiere, S., Beebe, A. Y. & Stone, H. A. Wetting of flexible fibre arrays. Nature 482, 510–513 (2012).
Bonaccurso, E. & Butt, H.-J. Microdrops on atomic force microscope cantilevers: evaporation of water and spring constant calibration. J. Phys. Chem. B 109, 253–263 (2006).
Jerison, E. R., Xu, Y., Wilen, L. A. & Dufresne, E. R. Deformation of an elastic substrate by a three-phase contact line. Phys. Rev. Lett. 106, 186103 (2011).
Style, R. W. & Dufresne, E. R. Static wetting on deformable substrates, from liquids to soft solids. Soft Matter 8, 7177–7184 (2012).
Lester, G. R. Contact angles of liquids at deformable solid surfaces. J. Colloid Interface Sci. 16, 315–326 (1961).
Shanahan, M. E. R. & de Gennes, P. G. Equilibrium of the Triple Line Solid/Liquid/Fluid of a Sessile Drop. Adhesion 11 ed. Allen K. W. 71–81Elsevier Applied Science (1987).
Shanahan, M. E. R. The influence of solid micro-deformation on contact angle equilibrium. J. Phys. D: Appl. Phys. 20, 945–950 (1987).
Limat, L. Straight contact lines on a soft, incompressible solid. Eur. Phys. J. E Soft Matter 35, 134 (2012).
Weijs, J. H., Andreotti, B. & Snoeijer, J. H. Elasto-capillarity at the nanoscale: on the coupling between elasticity and surface energy in soft solids. Soft Matter 9, 8494 (2013).
Marchand, A., Das, S., Snoeijer, J. H. & Andreotti, B. Contact angles on a soft solid: From Young’s law to Neumann’s law. Phys. Rev. Lett. 109, 236101 (2012).
White, L. R. The contact angle on an elastic substrate. 1. The role of disjoining pressure in the surface mechanics. J. Colloid Interface Sci. 258, 82–96 (2003).
Rusanov, A. I. Theory of wetting of elastically deformed bodies. I. Deformation with a finite contact-angle. Colloid J. USSR 37, 614–622 (1975).
Style, R. W. et al. Patterning droplets with durotaxis. Proc. Natl Acad. Sci. USA 110, 12541–12544 (2013).
Pericet-Camara, R. et al. Solid-supported thin elastomer films deformed by microdrops. Soft Matter 5, 3611–3617 (2009).
Style, R. W. et al. Universal deformation of soft substrates near a contact line and the direct measurement of solid surface stresses. Phys. Rev. Lett. 110, 066103 (2013).
Carré, A., Gastel, J.-C. & Shanahan, M. E. R. Viscoelastic effects in the spreading of liquids. Nature 379, 432–434 (1996).
Pu, G. & Severtson, S. J. Dependence of wetting behavior on the thickness of highly viscoelastic films. J. Phys. Chem. C 115, 18729–18735 (2011).
Kajiya, T. et al. Advancing liquid contact line on visco-elastic gel substrates: Stick-slip vs. continuous motions. Soft Matter 9, 454–461 (2013).
Pu, G. & Severtson, S. J. Water evaporation on highly viscoelastic polymer surfaces. Langmuir 28, 10007–10014 (2012).
Extrand, C. W. & Kumagai, Y. Contact angles and hysteresis on soft surfaces. J. Colloid Interface Sci. 184, 191–200 (1996).
Lopes, M. C. & Bonaccurso, E. Evaporation control of sessile water drops by soft viscoelastic surfaces. Soft Matter 8, 7875–7881 (2012).
Roman, B. & Bico, J. Elasto-capillarity: Deforming an elastic structure with a liquid droplet. J. Phys. Condens. Matter 22, 493101 (2010).
Levental, I. et al. Soft biological materials and their impact on cell function. Soft Matter 3, 299–306 (2007).
Discher, D. E., Janmey, P. & Wang, Y. L. Tissue cells feel and respond to the stiffness of their substrate. Science 310, 1139–1143 (2005).
Hersen, P. & Ladoux, B. Biophysics: Push it, pull it. Nature 470, 340–341 (2011).
Paszek, M. J. et al. Tensional homeostasis and the malignant phenotype. Cancer Cell 8, 241–254.
Engler, A. J., Sen, S., Sweeney, H. L. & Discher, D. E. Matrix elasticity directs stem cell lineage specification. Cell 126, 677–689 (2006).
Wells, R. G. The role of matrix stiffness in regulating cell behavior. Hepatology 47, 1394–1400 (2008).
Geoghegan, M. Wetting at polymer surfaces and interfaces. Prog. Polym. Sci. 28, 261–302 (2003).
de Gans, B. J. & Schubert, U. S. Inkjet printing of well-defined polymer dots and arrays. Langmuir 20, 7789–7793 (2004).
Bennett, M. R. & Hasty, J. Microfluidic devices for measuring gene network dynamics in single cells. Nat. Rev. Genet. 10, 628–638 (2009).
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves Springer (2003).
Chu, Y. S. et al. Hard-x-ray microscopy with Fresnel zone plates reaches 40 nm Rayleigh resolution. Appl. Phys. Lett. 92, 103119 (2008).
Chen, Y.-T. et al. Hard x-ray Zernike microscopy reaches 30 nm resolution. Opt. Lett. 36, 1269–1271 (2011).
Weon, B. M. et al. Colloid coalescence with focused x rays. Phys. Rev. Lett. 107, 018301 (2011).
Weon, B. M., Lee, J. S., Kim, J. T., Pyo, J. & Je, J. H. Colloidal wettability probed with X-ray microscopy. Curr. Opin. Colloid Interface Sci. 17, 388–395 (2012).
Chen, D., Cai, S., Suo, Z. & Hayward, R. C. Surface energy as a barrier to creasing of elastomer films: An elastic analogy to classical nucleation. Phys. Rev. Lett. 109, 038001 (2012).
Cabral, J. T. & Hudson, S. D. Microfluidic approach for rapid multicomponent interfacial tensiometry. Lab. Chip 6, 427–436 (2006).
Shuttleworth, R. The surface tension of solids. Proc. Phys. Soc. A 63, 444–457 (1950).
Butt, H.–J. A sensitive method to measure changes in the surface stress of solids. J. Colloid Interface Sci. 180, 251–260 (1996).
Style, R. W. et al. Traction force microscopy in physics and biology. Soft Matter 10, 4047–4055 (2014).
Ochsner, M. et al. Micro-well arrays for 3D shape control and high resolution analysis of single cells. Lab. Chip 7, 1074–1077 (2007).
Cesa, C. M. et al. Micropatterned silicone elastomer substrates for high resolution analysis of cellular force patterns. Rev. Sci. Instrum. 78, 034301 (2007).
Andrews, J. C. et al. A high resolution, hard x-ray bio-imaging facility at SSRL. Synchrotron Radiat. News 21, 17–26 (2008).
Pereiro, E., Nicolás, J., Ferrer, S. & Howells, M. R. A soft X-ray beamline for transmission X-ray microscopy at ALBA. J. Synchrotron Radiat. 16, 505–512 (2009).
Carrascosa, J. L. et al. Cryo-X-ray tomography of vaccinia virus membranes and inner compartments. J. Struct. Biol. 168, 234–239 (2009).
Rexnikova, E. et al. Transmission hard X-ray microscope with increased view field using planer refractive objectives and condensers made of SU-8 polymer. J. Phys. Conf. Ser. 186, 012070 (2009).
Weon, B. M. et al. Ablation and deposition of poly(dimethylsiloxane) with x-rays. Chemphyschem. 11, 115–118 (2010).
Acknowledgements
We thank Eric R. Dufresne and Robert W. Style for their helpful comments about this work. We also thank Guy K. German for preparing soft substrates. This research was financially supported by the Creative Research Initiatives (Functional X-ray Imaging) of MEST/NRF. Use of the Advanced Photon Source, an Office of Science User Facility operated for the US Department of Energy (DOE) Office of Science by Argonne National Laboratory, was supported by the US DOE under contract no. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
S.J.P., B.M.W. and J.H.J. designed the research; S.J.P., J.S.L., J.H.L. and J.K. performed the wetting experiments; S.J.P., B.M.W. and J.H.J. analysed the data; J.H.J. managed the project; S.J.P., B.M.W. and J.H.J. wrote the initial manuscript; and all authors discussed the results and commented for the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-3, Supplementary Tables 1-3, Supplementary Note 1. (PDF 913 kb)
Supplementary Movie 1
Wetting ridge growth for an EG 40% drop on a silicone gel (E ≈ 3 kPa). The wetting ridge shows a slow and linear growth tendency. See Figure 3 and text. (MOV 278 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Park, S., Weon, B., Lee, J. et al. Visualization of asymmetric wetting ridges on soft solids with X-ray microscopy. Nat Commun 5, 4369 (2014). https://doi.org/10.1038/ncomms5369
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms5369
This article is cited by
-
Direct force measurement of microscopic droplets pulled along soft surfaces
Nature Communications (2022)
-
Fluid separation and network deformation in wetting of soft and swollen surfaces
Communications Materials (2021)
-
Wetting transitions in droplet drying on soft materials
Nature Communications (2019)
-
Direct measurement of strain-dependent solid surface stress
Nature Communications (2017)
-
Floating mechanism of a small liquid marble
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.