Abstract
Unlike photons, which are conveniently handled by mirrors and optical fibres without loss of coherence, atoms lose their coherence via atom–atom and atom–wall interactions. This decoherence of atoms deteriorates the performance of atomic clocks and magnetometers, and also hinders their miniaturization. Here we report a novel platform for precision spectroscopy. Ultracold strontium atoms inside a kagome-lattice hollow-core photonic crystal fibre are transversely confined by an optical lattice to prevent atoms from interacting with the fibre wall. By confining at most one atom in each lattice site, to avoid atom–atom interactions and Doppler effect, a 7.8-kHz-wide spectrum is observed for the 1S0−3P1(m=0) transition. Atoms singly trapped in a magic lattice in hollow-core photonic crystal fibres improve the optical depth while preserving atomic coherence time.
Similar content being viewed by others
Introduction
Quantum metrology1 with atoms relies on the long coherence times of atoms and photons to perform measurements at the quantum limit, which finds broad applications including atomic clocks2, atom interferometers3, magnetometers4 and quantum simulators5. In particular, seeking minimally perturbed, optically-dense atomic samples6 has been a long-standing endeavour in atomic, molecular and optical physics, as the quantum projection noise (QPN)7 in the measurements reduces with the number of atoms as  , which improves sensitivities in spectroscopy8, optical magnetometry4 and the search for the permanent electric dipole moment (EDM)9. Since the atomic absorption cross-section of a resonant light with wavelength λ is given by σ0=3λ2/2π, a small beam radius is preferable for efficient coupling10 between atoms and photons. In a free-space Gaussian beam, however, as the Rayleigh range changes as
, which improves sensitivities in spectroscopy8, optical magnetometry4 and the search for the permanent electric dipole moment (EDM)9. Since the atomic absorption cross-section of a resonant light with wavelength λ is given by σ0=3λ2/2π, a small beam radius is preferable for efficient coupling10 between atoms and photons. In a free-space Gaussian beam, however, as the Rayleigh range changes as  , an effective interaction volume
, an effective interaction volume  rapidly decreases as the waist radius
rapidly decreases as the waist radius  . One then is confronted with severe trade-offs: a strong atom–photon interaction is available at the price of increased atom density n=Na/V, which causes harmful atom–atom interactions. Atoms in a cavity have been used to get rid of this constraint by enabling multiple interaction11,12 of photons Np with atoms Na inside a cavity mode volume
. One then is confronted with severe trade-offs: a strong atom–photon interaction is available at the price of increased atom density n=Na/V, which causes harmful atom–atom interactions. Atoms in a cavity have been used to get rid of this constraint by enabling multiple interaction11,12 of photons Np with atoms Na inside a cavity mode volume  , with L the length of the cavity.
, with L the length of the cavity.
Atoms coupled to optical fibres may offer an alternative, as their effective interaction length can be arbitrarily longer than the Rayleigh range zR. A strong coupling of spontaneous photons into the guided mode of a nanofibre was predicted and observed13. The evanescent trapping of atoms in the vicinity of the nanofibre allowed for an interface between atoms and guided modes14. A state-insensitive two-colour dipole trapping around the nanofibre was demonstrated15 to reveal the natural linewidth of the 6S1/2, F=4→6P3/2, F′=5 transition of Cs, by cancelling out the light shifts of trapping lasers. In contrast, hollow-core photonic crystal fibres (HC-PCFs)16 have been proven to confine thermal atoms or molecules together with the guided light inside its core over several metres, enabling the generation of optical nonlinearities at ultra-low optical power-levels, and sensitive spectroscopy on weak transitions17. For example, a 10-kHz precision was demonstrated for a saturated absorption spectroscopy of acetylene by extrapolating the zero pressure-shift18. To prevent atoms from interacting with the fibre walls, optical dipole trapping of atoms in HC-PCFs was applied to guide thermal Rb gas19, Bose condensed Na gas20 and laser-cooled Rb gas21. Removal of the light shift perturbation during absorption spectroscopy was demonstrated by temporarily turning off a guiding laser22.
However, in all the above configurations, the finest fibre-based spectroscopy that has so far been measured still exhibits a several-megahertz-wide spectral linewidth. This broad linewidth is set by the strong collision of the confined thermal molecules or atoms18,23 with the fibre core inner-wall, or by the natural linewidth of alkali atoms15,22. As such, the coherence of atoms or molecules longer than tens of nanoseconds in fibres remains a challenge. Targeting ultra-precision laser spectroscopy of atoms at a fractional uncertainty of 10−17 and beyond, which is regarded as a goal accuracy for next-generation atomic clocks24,25, we considered possible fibre-based configurations. Depending on the atom-wall distance, from tens of nanometres to tens of micrometres, the atom fibre–wall interactions change from van der Waals, Casimir-Polder and finally to thermal-bath regimes26. The van der Waals interaction strongly shifts atomic lines by as much as 10−10 of the fractional frequency-shift, for atoms trapped in the evanescent field13,14,15 at tens of nm from the nanofibres. To keep the atom–wall interaction-induced fractional frequency shift below 10−17, one has to keep the atom-fibre walls distance rc≳20 μm (see Methods).
Here we investigate the 1S0−3P1 transition of 88Sr atoms in a 1D optical lattice tuned to the magic condition, which confines atoms near the centre of the HC-PCF and in the Lamb-Dicke regime without introducing a light shift15,24,27. The moderately narrow linewidth γp=7.5 kHz of the transition28 offers an efficient probe to characterize atom–atom and atom–fibre interactions by its spectral line broadenings and shifts. Well-characterized collisional properties29 allow investigating the occupancy of atoms in lattices through the reinforced collisional shift by the resonant dipole–dipole interaction, while the total angular momentum J=1 of the upper state probes the fibre birefringence effects via the tensor light shift27. By carefully eliminating collisional shift and birefringence-induced light shift, we show that the atomic resonance frequency can be unaffected by the fibre within an uncertainty of 0.11 kHz or ≈3 × 10−13. Our investigations provide useful insight for designing fibre-based optical lattice clocks on the mHz-narrow 1S0−3P0 clock transitions30, where both the collisional and polarization-dependent light shift are expected to be suppressed by more than 3–7 orders of magnitude, depending on the isotopes to be used31.
Results
Experimental setup
Figure 1a shows our experimental set-up. 88Sr atoms are laser-cooled and trapped at a temperature of a few μK using a narrow line magneto-optical trap (MOT)32. A 32-mm-long kagome cladding lattice HC-PCF with hypocycloid core shape16,33,34 is placed near the MOT. The fibre covers the experimental wavelengths (689–914 nm) with loss figures of <650 dB km−1 and guides dominantly in the HE11 mode (see Fig. 1e-f and Methods). We couple optical lattice lasers at wavelength λL≈813 nm from both ends of the HC-PCF. The potential depth of the optical lattice is about 30 μK at the MOT position (z=−1.6 mm from the entrance end of the HC-PCF) and 300 μK inside the fibre. After loading approximately 104 atoms into the optical lattice, the atoms are adiabatically accelerated up to νm≈53 mm s−1 and transported inside the fibre hollow core to a position z. The atom acceleration and positioning is controlled by the frequency difference δν(t)=ν2(t)−ν1 of the lattice lasers, as outlined in Fig. 1a,b. For the adiabatic acceleration (deceleration) of atoms, we linearly chirp (≈2 kHz ms−1) the frequency difference δν(t) over 60 ms. The transport velocity νm is optimized to maximize the number of atoms that pass through the 32-mm-long fibre by considering the trade-offs: while shorter transit time  through the fibre reduces the collision losses, larger vm increases the heating loss of atoms, as we discuss below.
through the fibre reduces the collision losses, larger vm increases the heating loss of atoms, as we discuss below.
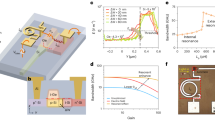
(a) Magneto-optically trapped (MOT) atoms are loaded into an optical lattice at around z=−1.6 mm from the fibre facet. (b) By tuning the frequency difference δν(t)=ν2−ν1 of the lattice lasers, the atoms are transported into a HC-PCF. A probe laser excites the 1S0−3P1(m=0) transition at 689 nm, with the transmitted light being fed into an avalanche photo-diode (APD) via a single-mode fibre (SMF) after eliminating lattice photons. HP: half-wave plate; DM: dichroic mirror; AOM: acousto-optic modulator. (c) Atom-expansion protocol. By slowly turning off one of the lattice lasers, we let atoms freely expand along the fibre axis guided by a dipole trap over  within tf=60 ms. Afterwards, the optical lattice is gradually recovered over 10 ms, while the probe-laser frequency is chirped from Δνp= −35 kHz to −70 kHz in 5 ms, to resettle atoms into lattice sites by Doppler and sideband cooling. (d) Atoms in the HC-PCF are confined radially and axially by the optical lattice, preventing atoms from interacting with the fibre-wall. (e) Microscope image of the kagome fibre. (f) Far-field pattern of the laser intensity passed through a 32-mm-long HC-PCF.
within tf=60 ms. Afterwards, the optical lattice is gradually recovered over 10 ms, while the probe-laser frequency is chirped from Δνp= −35 kHz to −70 kHz in 5 ms, to resettle atoms into lattice sites by Doppler and sideband cooling. (d) Atoms in the HC-PCF are confined radially and axially by the optical lattice, preventing atoms from interacting with the fibre-wall. (e) Microscope image of the kagome fibre. (f) Far-field pattern of the laser intensity passed through a 32-mm-long HC-PCF.
Lifetime of atoms in a fibre
The lifetime of the atoms in the fibre is of serious concern to discuss its potential applications, as glancing collisions with residual gases severely limit the coherence time of trapped atoms. The inset of Fig. 2 shows the lifetime τ=347 ms±8 ms of atoms trapped at z=23.4 mm. Figure 2 maps out the position-dependent lifetime of atoms along the fibre. The lifetime of τ=500 ms near the entrance of the fibre, which is close to that measured outside the fibre, decreases to τ=350 ms in the middle of the fibre. Using a glancing-collision model35 and taking into account the measured lifetimes and trap depth, we estimate the vacuum pressure in the middle and outside of the fibre to be Pin≈1.7 × 10−6 Pa and Pout≈1 × 10−6 Pa. The latter is in good agreement with the measured vacuum pressure, and the increase of the pressure in the fibre is reasonably accounted for by a small core radius rc=17 μm of the fibre and by the outgassing rate q per unit surface area of the fibre wall. By solving the 1D diffusion equation, we obtain the steady-state solution (∂PPCF/∂t=0) of the pressure inside the fibre as PPCF(z,l)=−qz(z−l)/(rcD)+Pout, for 0<z<l , with l being the length of the fibre and D the diffusion constant. On the basis of the estimated pressure PPCF(l/2, l) with l=32 mm, the pressure in the middle section of the fibre for an arbitrary length l would scale as PPCF(l/2, l) ≈7 × 10−4l2 Pa m−2+Pout. We expect that intensive baking of the fibre may reduce the outgassing rate q, thus extending the lifetimes of atoms for a longer fibre for future experiments.
The lifetime is determined by the number of atoms Na that pass through the fibre as a function of holding times Δt at a given z, where Na is observed by laser-induced fluorescence on the 1S0−1P1 transition at the exit of the fibre. The inset shows the decay of the number of atoms (empty circles) measured at z=23.4 mm. The red line shows the exponential fit to data points, which determines the lifetime to be τ=347 ms±8 ms. After loading atoms from the MOT at z=−1.6 mm, the atoms enter the 32-mm-long fibre at z=0 as indicated by the blue region. Empty circles show the lifetimes of atoms outside the fibre, which become longer as the atoms approach the fibre entrance, because of the increase of the potential depth. The lifetimes inside the fibre (filled circles) decrease towards the middle of the fibre due to the increase in collisions with residual gases. Asymmetric behaviour of the position-dependent lifetime with respect to the middle of the fibre (z=16 mm) may be responsible for the excess heating of atoms during transport, which makes lifetimes shorter for a given trap depth and background gas pressure as z increases. Error bars indicate the standard error (s.e.) in the fitting for each data point.
The above result also suggests that there is no extra heating loss of atoms in the fibre as long as atoms are held at the same position. However, we observe larger heating of atoms, as the transport velocity νm increases. At νm=53 mm s−1, the heating rate is estimated to be ~300 μK s−1 for the moving lattice potential depth of 180 μK. We attribute this to a parametric heating of atoms caused by a residual standing-wave field, which is created by a partial reflection (~0.5 %) of the lattice laser by a viewport. This standing-wave potential modulates the moving lattice potential by 7% at the frequency fm=2νm/λL~130 kHz, as atoms travel every λL/2. As νm increases, this frequency becomes closer to the parametric resonance condition36 fm=2flattice/n, where flattice≈300 kHz is the vibrational frequency of the lattice and n=4. To cope with this heating, we apply laser cooling during transport, which successfully reduces the heating loss of atoms.
Absorption spectroscopy
We perform absorption spectroscopy for atoms trapped at z~4 mm. The 1S0−3P1(m=0) intercombination transition at λp=689 nm is probed by a laser, whose linewidth and frequency drift per hour are both <1 kHz by referencing a cavity made of ultra-low expansion (ULE) glass. We apply a bias field of B0=(0.14 mT)êx perpendicular to the horizontal plane (see Fig. 1a) to define the quantization axis. The probe laser is linearly polarized with its electric field Ep parallel to B0 to excite the π transition. The differential light shift for the transition is given by27

where  is the differential polarizability, which depends on the lattice laser wavelength λL and its polarization ?L. The magic condition
is the differential polarizability, which depends on the lattice laser wavelength λL and its polarization ?L. The magic condition  , to remove the differential light shift, can be satisfied for 690 nm<λL<915 nm by tuning the tensor contribution of the light shift in the 3P1(m=0) state, which is determined by the angle θL of the linearly-polarized lattice laser ?L=EL/|EL| with respect to the quantization axis. It is noteworthy that, despite the fact that the HC-PCF guided mode exhibits a small longitudinal component Ez (see methods), this is cancelled out in the standing-wave configuration.
, to remove the differential light shift, can be satisfied for 690 nm<λL<915 nm by tuning the tensor contribution of the light shift in the 3P1(m=0) state, which is determined by the angle θL of the linearly-polarized lattice laser ?L=EL/|EL| with respect to the quantization axis. It is noteworthy that, despite the fact that the HC-PCF guided mode exhibits a small longitudinal component Ez (see methods), this is cancelled out in the standing-wave configuration.
We couple a probe intensity of Ip≈0.15I0 into the fibre, with I0=3 μW cm−2, the saturation intensity of the transition. The transmission through atoms in the fibre is coupled to an avalanche photodiode (APD), as shown in Fig. 1a, where the overall photon-counting efficiency is estimated to be 30%. We define the frequency-dependent optical depth as

where Δνp=νp−ν0 is the detuning of the probe laser. Here, we approximate the Bessel-mode profile of the guided mode to a Gaussian one with w0=11.8 μm (see Methods), and  assumes an atomic density distribution with wa≈2.0 μm, estimated from the atomic temperature and radial-trapping frequency of ≈1.3 kHz. Here, l=32 mm and rc=17 μm are the length and hollow-core radius of the fibre, respectively. Using the photon-counting rates with and without atoms, Πw and Πw/o, and the background count rate Πbk, the transmittance of the fibre is given by T=(Πw−Πbk)/(Πw/o−Πbk), which is used to derive the optical depth as OD(Δνp)=−ln T. The number of atoms in the fibre is given by Na≈1200·OD(0). To avoid excess light shifts during spectroscopy, we reduce the lattice intensity by one order of magnitude from that used during the atom transfer. The probing time of the transition is limited to 3 ms to reduce the photon-recoil heating loss of atoms out of the lattice potential.
assumes an atomic density distribution with wa≈2.0 μm, estimated from the atomic temperature and radial-trapping frequency of ≈1.3 kHz. Here, l=32 mm and rc=17 μm are the length and hollow-core radius of the fibre, respectively. Using the photon-counting rates with and without atoms, Πw and Πw/o, and the background count rate Πbk, the transmittance of the fibre is given by T=(Πw−Πbk)/(Πw/o−Πbk), which is used to derive the optical depth as OD(Δνp)=−ln T. The number of atoms in the fibre is given by Na≈1200·OD(0). To avoid excess light shifts during spectroscopy, we reduce the lattice intensity by one order of magnitude from that used during the atom transfer. The probing time of the transition is limited to 3 ms to reduce the photon-recoil heating loss of atoms out of the lattice potential.
Collisional shift and its suppression
Figure 3a shows the measured optical depth OD(Δνp) as a function of the probe laser frequency. The Lamb-Dicke confinement and the light-shift cancellation allow us to approach the natural linewidth of the transition. However, as shown by the red symbols in Fig. 3b,c, we observe a collisional shift and broadening (see methods) for OD(0)>0.8, which corresponds to the mean atom-occupation of each lattice site  . Here, the atom cloud length la is measured by the laser-induced fluorescence image of atoms, after extraction from the fibre by the moving lattice.
. Here, the atom cloud length la is measured by the laser-induced fluorescence image of atoms, after extraction from the fibre by the moving lattice.
(a) Absorption spectra with and without atomic expansion over lattice sites, as illustrated in the inset, are displayed by blue and red symbols, respectively, corresponding to a mean atom occupation of  and
and  . (b) Spectral linewidth and (c) shift as a function of OD(0). The error bars display the s.e. The atom number-dependent broadening and shift of the spectrum are suppressed by applying a lattice-expansion protocol, as shown by the blue symbols. Reducing OD(0)<0.8 for the original atom cloud length la≈700 μm, which corresponds to
. (b) Spectral linewidth and (c) shift as a function of OD(0). The error bars display the s.e. The atom number-dependent broadening and shift of the spectrum are suppressed by applying a lattice-expansion protocol, as shown by the blue symbols. Reducing OD(0)<0.8 for the original atom cloud length la≈700 μm, which corresponds to  , nearly suppresses collisions (see red circles). The red and blue dashed curves assume a collision shift coefficient of β=−1 × 10−9 Hz cm3. The data points indicated by the dotted rectangle correspond to the spectra shown in a.
, nearly suppresses collisions (see red circles). The red and blue dashed curves assume a collision shift coefficient of β=−1 × 10−9 Hz cm3. The data points indicated by the dotted rectangle correspond to the spectra shown in a.
To make the high optical depth compatible with reduced atomic interactions, we expand the atom cloud over the lattice sites in the fibre by temporarily turning off the lattice confinement for tf=60 ms, while maintaining the dipole trapping in the radial direction. The time chart outlined in Fig. 1c allows us to extend the cloud length to  , where we use an atomic velocity of
, where we use an atomic velocity of  , estimated from the Doppler width of 55 kHz. This procedure reduces the mean atom occupation from
, estimated from the Doppler width of 55 kHz. This procedure reduces the mean atom occupation from  down to
down to  (see the blue circles in Fig. 3a), while preserving an optical depth of OD(0) ≈2.5. The blue symbols in Fig. 3b,c show that the collisional broadening and shift are successfully suppressed by applying this procedure. However, the achieved linewidth of 11 kHz suggests that some unexplained broadening of several kHz still remains.
(see the blue circles in Fig. 3a), while preserving an optical depth of OD(0) ≈2.5. The blue symbols in Fig. 3b,c show that the collisional broadening and shift are successfully suppressed by applying this procedure. However, the achieved linewidth of 11 kHz suggests that some unexplained broadening of several kHz still remains.
Light polarization-dependent shift
To elucidate the source of this residual broadening, we investigate the birefringence of the HC-PCF. In addition, to improve the spatial resolution in the fibre, we reduce the collisional shift by limiting the number of atoms to Na<1,200, that is, OD(0)<1, instead of expanding atom clouds. Assuming the lattice laser polarization ?L to be parameterized by an angle θL as defined previously, equation (1) becomes  . For the lattice laser wavelength at λL=813 nm, the differential light shift can be removed by setting θL=46°. The angle sensitivity of the tensor light shift27
. For the lattice laser wavelength at λL=813 nm, the differential light shift can be removed by setting θL=46°. The angle sensitivity of the tensor light shift27  makes the light shift an efficient probe for the fibre birefringence.
makes the light shift an efficient probe for the fibre birefringence.
Figure 4a shows the lattice intensity-dependent light shift, where the gradient indicates the effective differential polarizability  . The blue filled and empty circles are measured for atoms inside (z813=3.7 mm) and outside (z0=−1.6 mm) the fibre, respectively. While the data confirm that the atomic resonance frequencies are unaffected by being guided in the fibre (as demonstrated by the IL→0 extrapolations that coincide at the same frequency), the change of polarizabilities inside
. The blue filled and empty circles are measured for atoms inside (z813=3.7 mm) and outside (z0=−1.6 mm) the fibre, respectively. While the data confirm that the atomic resonance frequencies are unaffected by being guided in the fibre (as demonstrated by the IL→0 extrapolations that coincide at the same frequency), the change of polarizabilities inside  and outside
and outside  the fibre indicates the presence of fibre-induced birefringence. Assuming an angle sensitivity of the tensor light shift,
the fibre indicates the presence of fibre-induced birefringence. Assuming an angle sensitivity of the tensor light shift,  corresponds to a polarization rotation of δθL≈0.5° between z0 and z813. We investigate the position-dependent birefringence effect throughout the fibre, which is found to be within δθL≈0.3° and, in particular, nearly constant for 0<z<8 mm. A relatively large deviation is found in the region of fibre support and clamp (see Fig. 1a), which may indicate the presence of pressure-induced fibre-birefringence. In the following measurements, and to be free from stress-induced effects, we focus our attention to the fibre position at around z≈4 mm.
corresponds to a polarization rotation of δθL≈0.5° between z0 and z813. We investigate the position-dependent birefringence effect throughout the fibre, which is found to be within δθL≈0.3° and, in particular, nearly constant for 0<z<8 mm. A relatively large deviation is found in the region of fibre support and clamp (see Fig. 1a), which may indicate the presence of pressure-induced fibre-birefringence. In the following measurements, and to be free from stress-induced effects, we focus our attention to the fibre position at around z≈4 mm.
(a) Intensity-dependent light shifts on the 1S0−3P1(m=0) transition for atoms inside (filled circles measured at z=3.7 and 4.3 mm) and outside (empty circles measured at z= −1.6 mm) the fibre at λL=813 nm (blue) and 914 nm (red) with θL=46° and 90°, respectively. For respective wavelengths, the data points are linearly fitted assuming respective y-intercepts,  and
and  , which are then taken to zero and their s.e. values are indicated by error bars at IL=0 with respective colours. The fitted gradient is a measure of the differential polarizabilities
, which are then taken to zero and their s.e. values are indicated by error bars at IL=0 with respective colours. The fitted gradient is a measure of the differential polarizabilities  , which are sensitive to the fibre birefringence effects. (b) A 7.8-kHz-wide spectrum, which agrees with the saturation broadened linewidth for Ip≈0.077I0, is observed for IL=37 kW cm−2 and λL=914 nm.
, which are sensitive to the fibre birefringence effects. (b) A 7.8-kHz-wide spectrum, which agrees with the saturation broadened linewidth for Ip≈0.077I0, is observed for IL=37 kW cm−2 and λL=914 nm.
To moderate the fibre-birefringence effect, further experiments are performed at a magic wavelength λL=914 nm, with θL=90°, where the angle dependence  appears only in second order. The filled and empty red circles in Fig. 4a show the resulting reduction in sensitivity measured at z914=4.3 mm and at z0=−1.6 mm, respectively. The slight change of the position from the measurements at λL=813 nm results from the lattice wavelength difference, which scales as
appears only in second order. The filled and empty red circles in Fig. 4a show the resulting reduction in sensitivity measured at z914=4.3 mm and at z0=−1.6 mm, respectively. The slight change of the position from the measurements at λL=813 nm results from the lattice wavelength difference, which scales as  , since we use the same detuning sequence δν(t) for the moving lattice. In this measurement, we simultaneously record the absorption spectra for five different intensity settings so as to minimize the influence of laser frequency drift in extrapolating the lattice intensity IL → 0. The data points are fit by
, since we use the same detuning sequence δν(t) for the moving lattice. In this measurement, we simultaneously record the absorption spectra for five different intensity settings so as to minimize the influence of laser frequency drift in extrapolating the lattice intensity IL → 0. The data points are fit by  , where νPCF(FS) and
, where νPCF(FS) and  denote the resonant frequency and the differential polarizability in the PCF or in free space (FS), respectively, and y0 assumes an offset frequency chosen to be zero in Fig. 4a. We evaluate the uncertainty of zero-intensity intercepts by the uncertainty of y0, which are 0.18 kHz and 0.11 kHz for 813 and 914 nm, respectively, as indicated by error bars at IL=0. The results indicate that the atomic resonance frequency is unaffected by the fibre with an uncertainty of ≈3 × 10−13.
denote the resonant frequency and the differential polarizability in the PCF or in free space (FS), respectively, and y0 assumes an offset frequency chosen to be zero in Fig. 4a. We evaluate the uncertainty of zero-intensity intercepts by the uncertainty of y0, which are 0.18 kHz and 0.11 kHz for 813 and 914 nm, respectively, as indicated by error bars at IL=0. The results indicate that the atomic resonance frequency is unaffected by the fibre with an uncertainty of ≈3 × 10−13.
Figure 4b shows a spectrum measured at the magic wavelength λL=914 nm with the lattice intensity of IL=37 kW cm−2 measured at z≈5.3 mm. The linewidth of 7.8(4) kHz agrees well with the saturation-broadened linewidth of 7.8 kHz for the probe laser intensity Ip≈0.077I0, demonstrating that there is no significant decoherence of atoms in the fibre at the kHz level. At λL=914 nm, we investigate the atomic resonance frequencies throughout the fibre, which are found to be within 2 kHz. This variation is partly due to the frequency drift of the probe laser and partly due to the spatial inhomogeneity of the fibre. The detailed investigations of fibre-dependent inhomogeneity, such as local stress on the fibre, charging effect and formation of patch potential on inner surface of the fibre, are underway.
Discussion
The scheme developed here offers a new and ideal platform for high-precision spectroscopy with enhanced signal-to-noise ratio, particularly suitable for the miniaturization of optical lattice clocks operated on the 1S0−3P0 clock transitions30. The systematic uncertainties of such clocks are essentially characterized by the nuclear spin I of an interrogated isotope, which at the same time decides its quantum statistical nature. Bosonic isotopes31,37,38,39, for example, 88Sr and 174Yb are highly susceptible to collisional shift; therefore, they certainly demand singly occupied lattices as demonstrated in a 3D optical lattice clock31. Recent observations suggest that, as the uncertainty of the clocks approaches 10−17, collisional interactions become a concern for clocks even with spin-polarized ultracold fermions40, such as 87Sr and 171Yb, where the s-wave collisions are suppressed. Our demonstrations of a singly-occupied lattice by expanding atoms in the fibre should be effective for both isotopes to reduce collisional shift while preserving the number of atoms or the QPN limit.
In contrast to free space optics, fibre optics requires special care for the state of light polarization, which is easily affected by mechanical stress or the inhomogeneity of the fibre. As the light polarization affects the light shift for the electronic states that have non-zero angular momentum F≠0, fermionic isotopes with half-integer nuclear spin become susceptible to fibre birefringence even in the clock states with total electronic angular momentum J=0. However, compared with the 3P1 state chosen here as a sensitive probe, the tensor shift in the clock transition of 87Sr is seven orders of magnitude smaller41, as it originates solely from its nuclear spin I=9/2. Our measurements, therefore, suggest that the tensor contribution is safely neglected in achieving 10−18 clock uncertainty.
A 32-mm-long HC-PCF, as employed here, will support as many as 105 lattice sites or Na≈105 atoms free from both collisions and light shifts, allowing to achieve a projection noise-limited stability of  , with τ the averaging time. This is in contrast with free-space lattice-clock experiments that employ ~103 atoms confined in less than 1-mm-long 1D lattices. Further increase in the number of atoms should be possible by extending the fibre length. Moreover, high optical depth and long atomic coherence time allow applying dispersive measurement of atoms42, quantum non-demolition (QND) measurement protocols and spin-squeezing of atoms during clock operation6. By heterodyning or homodyning the transmittance of a probe laser8, a quantum feedback scheme43 may be used to steer the probe laser frequency, instead of applying conventional projection measurements7. The strong coupling of atoms to guided modes allows the investigation of collective effects such as collective Lamb shifts44 and super-radiance45. In particular, super-radiant lasing46 on the clock transition or generation of narrow-line light source via the phase-matching effect47 may have potential to replace bulky reference cavities48,49 required for optical clocks, which will lead to significant miniaturization of optical clocks. Moreover, a fully populated 1D chain of 105 or more qubits sharing an optical bus of the fibre-guided mode could be used for quantum computing and simulation5 by providing individual spectroscopic access50 with a magnetic or electric field gradient.
, with τ the averaging time. This is in contrast with free-space lattice-clock experiments that employ ~103 atoms confined in less than 1-mm-long 1D lattices. Further increase in the number of atoms should be possible by extending the fibre length. Moreover, high optical depth and long atomic coherence time allow applying dispersive measurement of atoms42, quantum non-demolition (QND) measurement protocols and spin-squeezing of atoms during clock operation6. By heterodyning or homodyning the transmittance of a probe laser8, a quantum feedback scheme43 may be used to steer the probe laser frequency, instead of applying conventional projection measurements7. The strong coupling of atoms to guided modes allows the investigation of collective effects such as collective Lamb shifts44 and super-radiance45. In particular, super-radiant lasing46 on the clock transition or generation of narrow-line light source via the phase-matching effect47 may have potential to replace bulky reference cavities48,49 required for optical clocks, which will lead to significant miniaturization of optical clocks. Moreover, a fully populated 1D chain of 105 or more qubits sharing an optical bus of the fibre-guided mode could be used for quantum computing and simulation5 by providing individual spectroscopic access50 with a magnetic or electric field gradient.
In summary, we have demonstrated precision spectroscopy of atoms in a HC-PCF, investigating possible hurdles intrinsic to fibres, such as collision-limited lifetime, atom–atom interactions and fibre-induced birefringence. In the present experiment, the coherence time of the system is essentially limited by the natural lifetime of the 3P1 state. Further investigation of the coherence time up to a second is possible by interrogating the 1S0−3P0 clock transition30, which also reduces the sensitivity to fibre birefringence. The novel platform demonstrated here could have an immense impact on future metrology and quantum information sciences using miniaturized atomic devices.
Methods
Frequency shift due to atom fibre–wall interactions
The Casimir-Polder interaction energy51 between an atom with polarizability α and an infinite surface at a relatively large distance rc, for which the retardation limit is valid, is given by  with ε0 the vacuum permittivity. The coefficient Γ depends on the properties of the surface; Γ=1 for ideal metals and Γ<1 for dielectric materials. If one considers a photonic crystal with air-filling fraction P=0.94 as a dielectric with relative permittivity ε=1·p+εFS·(1−p), then Γ=(ε−1)/(ε+1)≈0.08 is expected, where we assume the static permittivity of fused silica to be εFS=3.8. The energy shift of an atom inside the HC-PCF can be larger than the value given by UCP by a geometric factor G~6, which accounts for the atom interaction with six walls (see Fig. 1e) when each of these walls is approximated by an infinite plane.
with ε0 the vacuum permittivity. The coefficient Γ depends on the properties of the surface; Γ=1 for ideal metals and Γ<1 for dielectric materials. If one considers a photonic crystal with air-filling fraction P=0.94 as a dielectric with relative permittivity ε=1·p+εFS·(1−p), then Γ=(ε−1)/(ε+1)≈0.08 is expected, where we assume the static permittivity of fused silica to be εFS=3.8. The energy shift of an atom inside the HC-PCF can be larger than the value given by UCP by a geometric factor G~6, which accounts for the atom interaction with six walls (see Fig. 1e) when each of these walls is approximated by an infinite plane.
The difference in polarizabilities for a Sr atom in the 1S0 and 3P0 states52 is Δα≈4·10−39 C m2V−1. For rc=20 μm, the frequency shift is given by  , which corresponds to a fractional clock shift Δν/ν0≈1.5 · 10−18. This estimate applies for the zero temperature limit. At room temperature, thermal effects become the same order as the zero fluctuations input. According to ref. 26, this gives a 3–4 times enhancement, and the atom–wall interaction corresponds to a fractional frequency shift of ~10−17.
, which corresponds to a fractional clock shift Δν/ν0≈1.5 · 10−18. This estimate applies for the zero temperature limit. At room temperature, thermal effects become the same order as the zero fluctuations input. According to ref. 26, this gives a 3–4 times enhancement, and the atom–wall interaction corresponds to a fractional frequency shift of ~10−17.
For the 1S0−3P1 transition, the fractional shift can be 20% larger, because of a 20% increase in the differential polarizability Δα. In this transition, however, the resonant dipole–dipole interaction may be more relevant53, because of the significantly larger dipole moment than that of the 1S0−3P0 clock transition. As the atom-wall distance is much larger than the transition wavelength, rc/(λp/2π)~180, the retardation effect dominates. Considering the current measurement precision of ~10−13, which is ~10−2γp with γp=7.5 kHz the natural linewidth, the atom–wall interactions can be safely neglected.
Coupling light into the hollow-core fibre
The probe and lattice lasers, which are sent through polarization-maintaining single-mode fibres (PM-SMF), are coupled to the HC-PCF using aspheric lens pairs. The output of the PM-SMF is collimated by a f=4.6 mm lens to pass through a vacuum viewport without aberrations and is then matched to the HE11 mode of the HC-PCF by a f=18.4 mm lens. Typically 90% of the laser power is transmitted through the 32-mm-long fibre. The far-field intensity pattern is nearly Gaussian as shown in Fig. 1f. The spatial mode after the HC-PCF is verified by recoupling it to another PM-SMF, where we achieve an overall (SMF-HC-SMF) coupling efficiency of 70%.
HC-PCF design and fabrication
The fibre is fabricated using the standard stack-and-draw technique. The cladding structure is that of a kagome-lattice with a pitch of 14 μm (Fig. 5b) and strut thickness of 196 nm (Fig. 5c). This is the smallest silica strut thickness so far reported for a hypocycloid core HC-PCF33. This allows the fibre to guide light with low loss for wavelengths as short as 400 nm (see Fig. 5a), and thus covering the experimental operating wavelengths of 813 and 689 nm with loss figures of 530 and 650 dB km−1, respectively.
HE11 mode intensity profile and electric field distribution
The fibre hollow core has a hypocycloid contour with inner radius rc~17 μm (ref. 33). Figure 6 shows the norm of the two polarization degenerate electric fields of the modes along the two axes of symmetry of the fibre core. The presented simulations are performed over a spectrum of 800–830 nm to cover our operating wavelength of 813 nm, where the mode size has a very moderate change with wavelength. The vertical dashed lines indicate the radial position of the field at e−1 of its maximum, corresponding to a mode-field (MF) radius of the HE11 mode of ~12.7 μm. This Bessel intensity transverse profile fits to a Gaussian profile with e−2 of the maximum radial position at w0=11.8 μm. The electric and magnetic fields for the fundamental core-mode HE11 are computed using the finite-element-method. Figure 7 shows the components of the electric E (V m−1) and magnetic B (T) fields, when the total optical power contained in the HE11 mode is set to 1 W. The results show that the magnitude of the longitudinal component Ez is almost 100 times smaller than the transverse components (Ex, Ey).
(a) Transverse profile of the simulated fibre structure. Rin and Rout are the axes along which the field is calculated. (b,c) HE11 electric field norm profile along the Rin (blue curve) and Rout (red curve) axes for y-polarization (b) and x-polarization (c). The electric field in V m−1 has been calculated for a total power of 1 W. The mode-field (MF) radius of the HE11 mode is ~12.7 μm, as indicated by vertical dashed lines. The horizontal dashed curves indicate the e−1 of the maximum field norm.
HE11 birefringence
The fabricated fibre core exhibits a small ellipticity, which results in a residual birefringence Δneff. Figure 8 shows the spectrum of the birefringence near the lattice laser wavelength 813 nm. The birefringence is found to be 9.6 × 10−8 (that is, a beat length of 8.4 m), which is more than one order of magnitude lower than the typical photonic bandgap HC-PCF17. It is noteworthy that, in addition to the intrinsic fibre form, the birefringence is also induced by mechanical and/or thermal stress. In the case of a photonic bandgap HC-PCF, the lateral pressure-induced birefringence was measured54 to be in the range of ∂Δneff/∂p~10−11 Pa−1.
Collision shifts
We evaluate the collision-shift  as
as

where β is the collision-shift coefficient, n1=1/ν is the atom density for a singly occupied lattice site with ν=7.8 × 10−13 cm3 and  assumes the Poisson distribution of atoms with mean occupancy
assumes the Poisson distribution of atoms with mean occupancy  . The red and blue dashed curves in Fig. 3c show
. The red and blue dashed curves in Fig. 3c show  , with β=−1 × 10−9 Hz cm3 to fit the corresponding data points, with red and blue filled circles. This collision-shift coefficient β agrees reasonably well with that measured previously by the JILA group29 βJILA= −1.3(3) × 10−9 Hz·cm3.
, with β=−1 × 10−9 Hz cm3 to fit the corresponding data points, with red and blue filled circles. This collision-shift coefficient β agrees reasonably well with that measured previously by the JILA group29 βJILA= −1.3(3) × 10−9 Hz·cm3.
Additional information
How to cite this article: Okaba, S. et al. Lamb-Dicke spectroscopy of atoms in a hollow-core photonic crystal fibre. Nat. Commun. 5:4096 doi: 10.1038/ncomms5096 (2014).
References
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon 5, 222–229 (2011).
Gerginov, V. et al. Long-term frequency instability of atomic frequency references based on coherent population trapping and microfabricated vapor cells. J. Opt. Soc. Am. B 23, 593–597 (2006).
Pereira Dos Santos, F. et al. Controlling the cold collision shift in high precision atomic interferometry. Phys. Rev. Lett. 89, 233004 (2002).
Budker, D. & Romalis, M. Optical magnetometry. Nat. Phys. 3, 227–234 (2007).
Bloch, I. Ultracold quantum gases in optical lattices. Nat. Phys. 1, 23–30 (2005).
Hammerer, K., Sørensen, A. S. & Polzik, E. S. Quantum interface between light and atomic ensembles. Rev. Mod. Phys. 82, 1041–1093 (2010).
Itano, W. M. et al. Quantum projection noise: population fluctuations in two-level systems. Phys. Rev. A 47, 3554–3570 (1993).
Bjorklund, G. C., Levenson, M. D., Lenth, W. & Ortiz, C. Frequency modulation (FM) spectroscopy. Appl. Phys. B 32, 145–152 (1983).
Romalis, M., Griffith, W., Jacobs, J. & Fortson, E. New limit on the permanent electric dipole moment of 199Hg. Phys. Rev. Lett. 86, 2505–2508 (2001).
Tey, M. K. et al. Strong interaction between light and a single trapped atom without the need for a cavity. Nat. Phys. 4, 924–927 (2008).
Tanji-Suzuki, H. et al. inAdvances In Atomic, Molecular, And Optical Physics Vol. 60, eds Berman P. R., Arimondo E., Lin C. C. 201–237Academic Press (2011).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Nayak, K. P. et al. Optical nanofiber as an efficient tool for manipulating and probing atomic fluorescence. Opt. Express 15, 5431–5438 (2007).
Vetsch, E. et al. Optical interface created by laser-cooled atoms trapped in the evanescent field surrounding an optical nanofiber. Phys. Rev. Lett. 104, 203603 (2010).
Goban, A. et al. Demonstration of a state-insensitive, compensated nanofiber trap. Phys. Rev. Lett. 109, 033603 (2012).
Wang, Y. Y., Wheeler, N. V., Couny, F., Roberts, P. J. & Benabid, F. Low loss broadband transmission in hypocycloid-core kagome hollow-core photonic crystal fiber. Opt. Lett. 36, 669–671 (2011).
Benabid, F. & Roberts, P. Linear and nonlinear optical properties of hollow core photonic crystal fiber. J. Mod. Opt. 58, 87–124 (2011).
Knabe, K. et al. 10 kHz accuracy of an optical frequency reference based on 12C2H2-filled large-core kagome photonic crystal fibers. Opt. Express 17, 16017–16026 (2009).
Takekoshi, T. & Knize, R. J. Optical guiding of atoms through a hollow-core photonic band-gap fiber. Phys. Rev. Lett. 98, 210404 (2007).
Christensen, C. A. et al. Trapping of ultracold atoms in a hollow-core photonic crystal fiber. Phys. Rev. A 78, 033429 (2008).
Vorrath, S., Möller, S. A., Windpassinger, P., Bongs, K. & Sengstock, K. Efficient guiding of cold atoms through a photonic band gap fiber. New J. Phys. 12, 123015 (2010).
Bajcsy, M. et al. Laser-cooled atoms inside a hollow-core photonic-crystal fiber. Phys. Rev. A 83, 063830 (2011).
Perrella, C., Light, P., Stace, T., Benabid, F. & Luiten, A. High-resolution optical spectroscopy in a hollow-core photonic crystal fiber. Phys. Rev. A 85, 012518 (2012).
Katori, H. Optical lattice clocks and quantum metrology. Nat. Photon 5, 203–210 (2011).
Gill, P. When should we change the definition of the second? Phil. Trans. Roy. Soc. A 369, 4109–4130 (2011).
Derevianko, A., Obreshkov, B. & Dzuba, V. A. Mapping out atom-wall interaction with atomic clocks. Phys. Rev. Lett. 103, 133201 (2009).
Ido, T. & Katori, H. Recoil-free spectroscopy of neutral Sr atoms in the Lamb-Dicke regime. Phys. Rev. Lett. 91, 053001 (2003).
Drozdowski, R., Ignaciuk, M., Kwela, J. & Heldt, J. Radiative lifetimes of the lowest 3P1 metastable states of Ca and Sr. Z. Phys. D 41, 125–131 (1997).
Ido, T. et al. Precision spectroscopy and density-dependent frequency shifts in ultracold Sr. Phys. Rev. Lett. 94, 153001 (2005).
Katori, H., Takamoto, M., Pal'chikov, V. G. & Ovsiannikov, V. D. Ultrastable optical clock with neutral atoms in an engineered light shift trap. Phys. Rev. Lett. 91, 173005 (2003).
Akatsuka, T., Takamoto, M. & Katori, H. Optical lattice clocks with non-interacting bosons and fermions. Nat. Phys. 4, 954–959 (2008).
Katori, H., Ido, T., Isoya, Y. & Kuwata-Gonokami, M. Magneto-optical trapping and cooling of strontium atoms down to the photon recoil temperature. Phys. Rev. Lett. 82, 1116–1119 (1999).
Bradley, T. D. et al. Optical properties of low loss (70 dB/km) hypocycloid-core kagome hollow core photonic crystal fiber for Rb and Cs based optical applications. J. Lightwave Technol. 31, 2752–2755 (2013).
Debord, B. et al. Hypocycloid-shaped hollow-core photonic crystal fiber Part I: Arc curvature effect on confinement loss. Opt. Express 21, 28597–28608 (2013).
Steane, A. M., Chowdhury, M. & Foot, C. J. Radiation force in the magneto-optical trap. J. Opt. Soc. Am. B 9, 2142–2158 (1992).
Friebel, S., D’Andrea, C., Walz, J., Weitz, M. & Hänsch, T. W. CO2-laser optical lattice with cold rubidium atoms. Phys. Rev. A 57, R20–R23 (1998).
Baillard, X. et al. Accuracy evaluation of an optical lattice clock with bosonic atoms. Opt. Lett. 32, 1812–1814 (2007).
Barber, Z. W. et al. Direct excitation of the forbidden clock transition in neutral 174Yb atoms confined to an optical lattice. Phys. Rev. Lett. 96, 083002 (2006).
Lisdat, C., Winfred, J., Middelmann, T., Riehle, F. & Sterr, U. Collisional losses, decoherence, and frequency shifts in optical lattice clocks with bosons. Phys. Rev. Lett. 103, 090801 (2009).
Bishof, M. et al. Resolved atomic interaction sidebands in an optical clock transition. Phys. Rev. Lett. 106, 250801 (2011).
Westergaard, P. G. et al. Lattice-Induced Frequency Shifts in Sr Optical Lattice Clocks at the 10−17 Level. Phys. Rev. Lett. 106, 210801 (2011).
Lodewyck, J., Westergaard, P. G. & Lemonde, P. Nondestructive measurement of the transition probability in a Sr optical lattice clock. Phys. Rev. A 79, 061401 (2009).
Wiseman, H. M. & Milburn, G. J. Quantum Measurement and Control Cambridge University Press (2010).
Scully, M. O. Collective Lamb shift in single photon Dicke superradiance. Phys. Rev. Lett. 102, 143601 (2009).
Gross, M. & Haroche, S. Superradiance: an essay on the theory of collective spontaneous emission. Phys. Rep. 93, 301–396 (1982).
Meiser, D., Ye, J., Carlson, D. R. & Holland, M. J. Prospects for a Millihertz-Linewidth Laser. Phys. Rev. Lett. 102, 163601 (2009).
Yu, D. & Chen, J. Optical Clock with Millihertz Linewidth Based on a Phase-Matching Effect. Phys. Rev. Lett. 98, 050801 (2007).
Kessler, T. et al. A sub-40-mHz-linewidth laser based on a silicon single-crystal optical cavity. Nat. Photon 6, 687–692 (2012).
Jiang, Y. Y. et al. Making optical atomic clocks more stable with 10−16-level laser stabilization. Nat. Photon 5, 158–161 (2011).
DeMille, D. Quantum computation with trapped polar molecules. Phys. Rev. Lett. 88, 067901 (2002).
Lifshitz, E. & Pitaevskii, L. Statistical Physics Part 2, Landau and Lifshitz Course of Theoretical Physics Vol. 9, Pergamon Press (1980).
Safronova, M. S., Porsev, S. G., Safronova, U. I., Kozlov, M. G. & Clark, C. W. Blackbody-radiation shift in the Sr optical atomic clock. Phys. Rev. A 87, 012509 (2013).
Le Kien, F. & Hakuta, K. Spontaneous radiative decay of translational levels of an atom near a dielectric surface. Phys. Rev. A 75, 013423 (2007).
Pang, M. & Jin, W. A hollow-core photonic bandgap fiber polarization controller. Opt. Lett. 36, 16–18 (2011).
Acknowledgements
This work received support partly from the JSPS through its FIRST Program and from the Photon Frontier Network Program of MEXT, Japan. We thank N. Nemitz for a careful reading of the manuscript. F.B. acknowledges support from ‘Agence Nationale de Recherche’. F.N. is partially supported by the RIKEN iTHES Project, MURI Center for Dynamic Magneto-Optics, JSPS-RFBR contract No. 12-02-92100, and Grant-in-Aid for Scientific Research (S).
Author information
Authors and Affiliations
Contributions
H.K. envisaged and initiated the experiments. H.K., T.T. and S.O. designed the apparatus and experiments. S.O. and T.T. carried out the experiments and analysed the data. S.O., T.T. and H.K. discussed experimental results and equally contributed to the experiments. F.B. and T.B. designed and fabricated the fibre for the experimental requirements, and L.V. calculated the fibre modal fields. Z.M., V.Y. and F.N. calculated the atom–wall interactions, and all authors participated in discussions and the writing of the text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Okaba, S., Takano, T., Benabid, F. et al. Lamb-Dicke spectroscopy of atoms in a hollow-core photonic crystal fibre. Nat Commun 5, 4096 (2014). https://doi.org/10.1038/ncomms5096
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms5096
This article is cited by
-
Low-loss single-mode hybrid-lattice hollow-core photonic-crystal fibre
Light: Science & Applications (2021)
-
Large array of Schrödinger cat states facilitated by an optical waveguide
Nature Communications (2020)
-
Single-Photon Transport in One-Dimensional Coupled-Resonator Waveguide with Second-Order Nonlinearity oupling to a Nanocavity Containing a Two-Level Atom and Kerr-Nonlinearity
International Journal of Theoretical Physics (2020)
-
Optical rotation conveyor belt based on a polarization-maintaining hollow-core photonic crystal fiber
Optical Review (2020)
-
Superradiance from lattice-confined atoms inside hollow core fibre
Communications Physics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.