Introduction

High-angle grain boundaries (GBs) could enhance the strength of crystalline materials by hindering dislocation motion under monotonic loading1,2. However, the dislocation pileups could generate stress concentration and strain incompatibility at the GB, which facilitates the GB cracking under cyclic loading3,4,5. And it is found that the GB is always the preferential fatigue cracking site intrinsically rather than the slip band (SB) no matter whatever angle the GB is inclined at in the bicrystals3. By suitable manipulation of the GB configuration, such as increasing the fractions of coincidence site lattice boundaries, the intergranular degradation could be improved and strong and ductile polycrystals would be developed6,7. As a special coincidence site lattice boundary, the coherent twin boundaries (TBs) from the micro to angstrom scale are widely described both theoretically and experimentally to play a significant role in the plastic deformation of materials8,9,10,11,12. Due to the special crystallographic characteristics, the TB possesses specific interactions with the dislocations13. The TB could provide barrier to the dislocation motion like the conventional GB to enhance the strength9,10,13 and it is also a slip plane, which could accommodate10,11,13 or be penetrated by the dislocations12,14,15 to improve the plasticity. On one hand, the incorporation of nanoscale TBs into materials can partly turn the trade-off relationship between the strength and ductility of the nano-grained materials9,10,11,12,16. On the other hand, the dislocations could glide in-between the twins, transfer across or slip parallel to the TB, which could be switched by changing the loading direction with respect to the TB, resulting in different mechanical properties of the nano-twinned copper17,18,19. On the basis of the worldwide researches on the unidirectional deformation, it is urgent to investigate the fatigue cracking mechanisms of the TB, which is of great significance in scientific research and engineering application. Different slip systems near the TB were observed in the fatigued coarse-grained copper20 and different TB-dislocation interactions could cause fatigue damage of different degrees to the TB in the polycrystals21,22. However, previous researches mainly employed polycrystalline aggregates with many kinds of planar defects. The existence of numerous grains with complicated stress conditions obscures the individual role of the TB in the mechanical properties. Therefore, this raises the intriguing scientific questions: what is the original role of the TB with cyclic loading and is there any controllability of the TB cracking distinct from the high-angle GB?

A series of grown bicrystals with a TB as its sole internal boundary were employed in the present investigation, wherein the angle between the TB plane and the loading direction of the twinned bicrystal (θ) is varied from 0° to 90° as depicted in Fig. 1a. The bicrystals with the TB parallel, perpendicular and inclined at 45° to the loading direction, respectively, are representative cases and their primary slip systems are sketched in Fig. 1. The twin components are related with each other by reflection through the TB plane, which is set as plane ACD. The double Thompson tetrahedron is illustrated in Fig. 1f with the tetrahedrons above and below the TB representing slip systems in the matrix and twin grains, respectively13. When the TB is parallel to the loading direction, the two component grains have the same crystallographic orientation and same Schmid factor distribution. The slip systems with the highest Schmid factor in both the component grains are always the ones whose slip direction is parallel to the TB plane with the slip plane intersecting with the TB23 as depicted in Fig. 1c. The primary slip systems could be the slip vector AC on the slip plane ABC in the matrix grain corresponding with the slip vector A′C′ on the slip plane A′B′C′ in the twin grain. This kind of slip system is denoted as S1 in this study. Usually, when the TB is inclined at 45° to the loading direction, the primary slip planes in both component grains are parallel to the TB plane and their slip directions are parallel to each other as displayed in Fig. 1d. For instance, the slip vectors in both the component grains could be AC and A′C′ on planes ACD and A′C′D′, respectively. This kind of slip system is named as S2. As to the bicrystal with the TB perpendicular to the loading direction, naturally the loading directions of the two component grains are along the normal of the TB plane, <111> direction, which is a multiple-slip orientation and six slip systems have the same Schmid factor of 0.272. The primary slip system with slip plane and slip direction intersecting with the TB plane is named as S3. The representative example is sketched in Fig. 1e with BD on slip plane BCD and B′D′ on the slip plane B′C′D′ in both of the component grains. The above three kinds of twinned bicrystals manifest the three major interaction modes between incoming slip and TB. Generally, there might be arbitrary combinations of the above three slip systems. It is necessary to investigate the fatigue cracking behaviours of bicrystals whose primary slip systems differ from the above three kinds. Consequently five kinds of bicrystals with a TB inclined at 0°, 30°, 45°, 60° and 90°, respectively, were designed and applied in this study and the possible interactions between the TB and primary slip during the cyclic deformation are all taken into consideration using all the above twinned bicrystals.

Figure 1: The orientations and primary slip systems of the specimens.
figure 1

(a) Orientation and grain boundary (GB) map with the cutting ways of the specimens. (b) {111} pole figure of the bicrystal; primary slip systems predicted by Schmid’s law for the bicrystals with a twin boundary (TB) (c) parallel (d) inclined at 45° and (e) perpendicular to the loading direction, respectively. (f) The double Thompson tetrahedron.

Full size image

Here we investigate the cyclic deformation and fatigue cracking behaviours of the twinned bicrystals with the help of scanning electron microscope (SEM) observation and electron channelling contrast (ECC) imaging method. The connections between the TB inclination angles and the fatigue cracking mechanisms are determined. When the TB is parallel or perpendicular to the loading direction, the SB cracks nucleate first; when the TB is inclined to the loading direction, the TB crack initiates preferentially. Obviously, this endows us with the control over the fatigue cracking behaviours of copper bicrystals with a TB.

Results

SEM and ECC results of coaxial twinned bicrystal

The slip morphologies with fatigue cracks and the corresponding dislocation arrangement of the twinned bicrystals are shown in Figs 2 and 3. The white arrows in the upper-right corner of the figures represent the loading direction of each specimen. Which kind of slip system was activated has been verified by combined consideration of the Schmid factors and the angles between the SBs and the loading direction on the two orthogonal specimen surfaces.

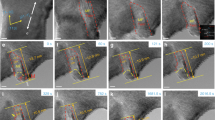
Figure 2: Surface morphologies and dislocation arrangements of the bicrystals with a TB parallel or perpendicular to the loading direction.
figure 2

(a) Slip morphologies with fatigue cracks of the bicrystal with the TB parallel to the loading direction. Scale bar, 50 μm. (b) Dislocation arrangements of the bicrystals with the TB parallel to the loading direction. Scale bar, 5 μm. (c) Slip morphologies with fatigue cracks of the bicrystal with the TB perpendicular to the loading direction. Scale bar, 10 μm. (d) Dislocation arrangements of the bicrystals with the TB perpendicular to the loading direction. Scale bar, 10 μm.

Full size image
Figure 3: Surface morphologies and dislocation arrangements of the bicrystals with an inclined TB.
figure 3

(a) Slip morphologies with fatigue cracks (scale bar, 20 μm) and (b) the dislocation arrangement of the bicrystal with a TB inclined at 45° (scale bar, 5 μm). (c) Slip morphologies with fatigue cracks (scale bar, 10 μm) and (d) the dislocation arrangement of the bicrystal with a TB inclined at 30° (scale bar, 5 μm). (e) Slip morphologies with fatigue cracks (scale bar, 20 μm) and (f) the dislocation arrangement of the bicrystal with a TB inclined at 60° (scale bar, 5 μm).

Full size image

The deformation morphology and the dislocation arrangement of the fatigued bicrystal with the TB parallel to the loading direction are displayed in Fig. 2a,b, respectively. It can be seen from Fig. 2a that the SBs belonging to the S1 slip systems appear and no secondary SB is found23,24. The SBs can transfer across the TB with mirror symmetric relationship which is consistent with the schematic plot in Fig. 1c. The fatigue cracks nucleate preferentially along the primary SBs similar to single crystals3,5. Besides, some SB cracks exist in the grain interior and some SB cracks even pass through the TB as detected before23,24. As exhibited in Fig. 2b, some dislocation walls form in both of the component grains, which correspond with the surface persistent SBs like in the single crystal25 and some dislocation walls match up well across the TB14. On the whole, there is little difference in the SB distribution between areas near and far away from the TB and so is the dislocation arrangement. A single TB parallel to the loading direction has little impact on the cyclic deformation and fatigue cracking behaviours of the bicrystal and the TB would not form fatigue crack, which is different from the bicrystals or polycrystals with high-angle GBs3.

SEM and ECC results of bicrystal with a perpendicular TB

When the TB is perpendicular to the loading direction, the S3 slip systems have the highest Schmid factors. The surface deformation morphology is shown in Fig. 2c. More than one slip systems are activated on the surface due to the multiple-slip orientation of the two component grains. The normal of the TB plane deviates from the loading direction slightly and then the slip morphology in the matrix grain is not exactly the same as that in the twin grain. The TB poses great barrier to the dislocation motion in this case20 and with the cyclic deformation, the strain gradually concentrates in the grain interior. Thus it is observed that the fatigue cracks nucleate along the densely distributed SBs in the grain interior on one side of the TB as that found in single crystal26,27; in addition, there are already some fatal fatigue cracks formed along the SBs in areas close to the transition area of the specimen. As shown in Fig. 2d, on one side of the TB, there are some parallel dislocation walls corresponding with dense SBs in the grain interior while there are some veins adjacent to the TB corresponding with the sparse SBs. On the other side of the TB, dislocation cell or ladder structure exists, which is concerned with the coplanar slip systems as detected before28. It is clear that though there is pilling-up of dislocations at the TB which is perpendicular to the loading direction, the fatigue crack still initiates preferentially at the SBs rather than at the TB, different from the high-angle GBs3.

SEM and ECC results of bicrystals with an inclined TB

Above all, when the TB is parallel or perpendicular to the loading direction, neither does the strain concentration nor does the fatigue cracking occur at the TB. The fatigue crack nucleates along the SBs in the grain interior. However, quite distinct fatigue cracking behaviours occur in the bicrystals with an inclined TB as displayed in Fig. 3. When the TB is inclined at 45° to the loading direction, as demonstrated in Fig. 3a, SBs in both the component grains are parallel to the TB, which is in accordance with the S2 slip systems sketched in Fig. 1d. Surprisingly, dense SBs are localized near the TB, generating a TB affected zone. The localized strain near the TB should be higher than that of the whole specimen29,30. The corresponding dislocation arrangement is shown in Fig. 3b. It is well-known that matrix veins form in the early stage of cyclic deformation and with cyclic deformation, the dislocation ladders appear31,32. There are already some dislocation ladders formed near the TB while it still exhibits as dislocation patches in the grain interior far away from the TB which is also an indication of strain localization. The dislocation ladders in the matrix grain have good correspondence across the TB with the ladders in the twin grain. With cyclic deformation, the dislocation configuration evolves more quickly near the TB which is consistent with the slip behaviour. Unlike the high-angle GB, there is no SB impingement on the TB, but the fatigue crack still nucleates first along the TB readily as indicated in Fig. 3a.

The slip morphologies with fatigue crack for the other two bicrystals with an inclined TB are displayed in Fig. 3c,e. The initial fatigue cracks form along the TB for both cases like the bicrystal with a TB inclined at 45°. Nevertheless, not all the SBs are localized at the TB, some SBs belonging to the S1 or S3 slip systems intersecting with the TBs also appear in the grain interior on one or two sides of the TB. When the TB is inclined at 30° or 60° to the loading direction, the Schmid factors of the S2 slip systems are not the highest in the two component grains. Unexpectedly, SBs parallel to the TB are activated in the TB affected zone during cyclic deformation as displayed in Fig. 3c,e which might be concerned with the strain compatibility and stress enhancement near the TB29,33. As shown in Fig. 3d with the ECC result of the bicrystal with a TB inclined at 30°, there are veins in the areas far away from the TB while there are some dislocation cells surrounding the TB demonstrating remarkable strain localization. The dislocation arrangement of the bicrystal with a TB inclined at 60° is displayed in Fig. 3f. There are some dislocation ladders with good correspondence across the TB. It is also observed that there is a matchup between the dislocation ladders or cells across the TB in the bicrystal when the TB is inclined at 30° to the loading direction and dislocation cells or labyrinths also form first near the TB which is inclined at 60°. Thus when the TB is inclined at 30°, 45° or 60° to the loading direction, the S2 slip systems parallel to the TB plane are easily activated around the TB during cyclic deformation with pronounced fatigue cracking at TB eventually.

Discussion

Generally, the intergranular fatigue cracking is interpreted in the way of dislocation impingement with strain incompatibility and stress concentration3,4,5. Since the TB could be penetrated by the S1 SBs14,15, there is good strain compatibility near the TB which is parallel to the loading direction. So the TB shows higher fatigue cracking resistance than high-angle GB and the fatigue crack nucleates along the SB like in single crystals3,5. Whereas in the bicrystal with the TB perpendicular to the loading direction, the S3 SBs would pile up at the TB and could also penetrate through the TB partially34. The difference between the Ω of corresponding S3 slip systems in both the component grains is low, which generates high opportunity of dislocation penetration and good strain compatibility at the TB21,22. Then it shows the similar fatigue cracking behaviour to its component single crystal with preferential SB cracking and the TB perpendicular to the loading direction shows high fatigue cracking resistance.

For the bicrystals with an inclined TB, the S2 SBs are localized at the TB. Though they do not cause impingement to the TB, the S2 SBs play the crucial role in the TB shear fatigue cracking. Numerous vacancies could form along the TB or the SBs by the annihilation of edge dislocations with opposite signs during cyclic deformation5 different from unidirectional deformation. And the vacancies will concentrate and precipitate to form micro-cracks which would grow into the fatigue cracks afterward35 as illustrated in Fig. 4. The increase of the vacancy density dρv in an increment of shear strain dγ could be estimated as the density of annihilated edge dislocations 5:

Figure 4: The sketch for the dislocation motion and the crack formation along the slip band and the TB.
figure 4

(a) Dislocation cross-slip in the slip bands (SBs) in the grain interior. (b) The vacancies aggregate in the SBs to form the SB crack. (c) The dislocations from the two component grains transfer to the TB by cross-slip. (d) The vacancies aggregate on the TB to form the TB crack.

Full size image

wherein, ρe is the dislocation density in the persistent SB walls and ye is the distance for two edge dislocation to annihilate and b denotes the Burgers vector. According to the Taylor’s equation36, it could be derived that:

wherein α is constant, G is the shear modulus, τ is the cyclic shear stress. Then Equation (1) could be transformed into:

Usually the strain is not homogeneously distributed along the whole specimen and there is strain localization in the fatigued materials. It is believed that the dislocations in the SBs spread homogeneously all over the specimen and so do the vacancies as illustrated in Fig. 4a,b. However, it could be derived from the present experimental results that the dislocations tend to transfer to the TB plane by cross-slip as illustrated in Fig. 4c and the TB allows room for the dislocation storage to accommodate high plastic strain37. Numerous vacancies would generate on the TB or in the close proximity of the TB ascribed to the annihilation of the dislocations of the S2 slip systems. Subsequently the vacancy reaches a much higher density locally on the TB than the SBs in the grain interior as shown in Fig. 4d. Therefore, the degree of the vacancy aggregation along the TB could be expressed as:

The parameter η is introduced to characterize the degree of the strain localization. The increase in the vacancy density per cycle Δρv could be obtained by integration of Equation (4). When the vacancy density along the interface increases to the critical value, C, the fatigue crack initiates. The critical vacancy density could be considered as the same for the SB and TB cracks in one bicrystal specimen because both of them nucleate along the {111} plane. Thus, the critical cycles for the fatigue cracking could be expressed as:

The positions with high τ and η are the preferential fatigue cracking sites with lower Nc. The actual cycles for the fatigue cracking could not be given by the above analysis, but it could help explain which position would form fatigue cracks preferentially in a bicrystal with an inclined TB.

Apparently, S1 slip systems generate little damage to the TB parallel to the loading direction and so do the S3 slip systems to the TB perpendicular to the loading direction; while S2 slip systems bring shear damage to the TB which would lead to the final TB fatigue cracking. The TB orientation and the operated slip systems are interrelated and affect the fatigue cracking behaviours of the twinned bicrystals. The distribution ranges of the Schmid factors for the three kinds of slip systems are illustrated in Fig. 5 when the TB is inclined at different angles (0°–90°) to the loading direction. The black solid and dashed lines represent the upper and lower limits of the Schmid factors for the S1 slip systems, respectively, while the red ones display that for the S2 slip systems and the blue ones show that for the S3 slip systems. Wherein, the Schmid factors of the three kinds of slip systems for the employed bicrystals are illustrated by half-filled circles with corresponding colours. Then by combining the calculation and experimental results, the fatigue cracking behaviours of the twinned bicrystals with all possible TB inclinations are summarized in Fig. 6.

Figure 5: The Schmid factor distribution of the twinned bicrystals.
figure 5

The solid and dashed lines with different colors represent the value ranges for the Schmid factors of the three kinds of slip systems, respectively, in both of the component grains with the TB inclinations changing from 0° to 90°. The Schmid factors of the three kinds of slip systems for the employed bicrystals are illustrated by half-filled circles with corresponding colors.

Full size image
Figure 6: General fatigue cracking mechanisms of the twinned bicrystals with all possible TB inclinations (0° to 90°).
figure 6

The fatigue cracking behaviours are shown in the upper part of the figure and the schemes for the corresponding slip systems are displayed in the lower part. In regions I and V, S1 and S3 slip systems operate easily and there is good strain compatibility at the TB, therefore the fatigue cracks nucleate along the SBs first; in regions II–IV, the S2 slip systems operate easily and concentrate at the TB which leads to the preferential shear fatigue cracking at the TB.

Full size image

In region I when θ is lower than θ1, due to the highest Schmid factors, the S1 slip systems can be activated easily on both sides of the TB as the sketch shown in Fig. 6. While in region V when θ is higher than θ2, the S3 slip systems have the highest Schmid factor Ω and will operate in the grain interior. The S1 and S3 slip systems will undertake the main cyclic deformation in the two cases respectively and both of them could pass through the TB generating slight pilling-up of dislocations and good strain compatibility at the TB. During cyclic deformation, the vacancy generation prevails in the SBs which will lead to the final SB fatigue cracking preferentially as the SEM images shown in Fig. 6. It can be obtained that θ1 is lower than 25° and θ2 is larger than 70° on the basis of our available experimental results and the crystallographic analysis in Fig. 5, which need more quantitative studies in the future. In region III when θ is near 45°, S2 slip systems possess the highest Schmid factors and operate easily on both sides of the TB. In regions II and IV, the shear stress of S2 slip systems may not be the highest as in some of the present bicrystal specimens. Therefore S1 or S3 slip systems may also appear in the grain interior due to their relatively high Schmid factors. However, the S2 slip systems can always be easily activated in the vicinity of the TB with stress enhancement as evidenced by our experimental results. It could be inferred from Equation (4) that the local strain localization and higher stress would cause the higher vacancy concentration near the TB due to the annihilation of the dislocations from the S2 slip systems. Eventually, shear fatigue crack initiates along the TB preferentially in the three regions II–IV. Interestingly, the present TB cracking in the bicrystals originates from the shear damage caused by the S2 slips which obviously differs from the conventional GB cracking caused by slip impingement.

On the basis of the experimental results and analysis above, the dislocation behaviours and fatigue cracking mechanisms of the twinned bicrystal are found to vary with the TB inclination angles. The TBs in regions I and V exhibit higher fatigue cracking resistance under cyclic deformation and the SB cracks nucleate first. Besides, they can provide strengthening effect to the materials under unidirectional deformation since S1 and S3 slips become hard slip modes which can contribute to the higher yield stress of polycrystals17,18,19. In the central three regions II–IV, the shear TB crack nucleates preferentially and the S2 slip systems play the crucial role because they concentrate at the TB and bring shear damage to the TB. Meanwhile, the S2 slip systems become the soft slip mode and can lead to the lower strength of polycrystals with inclined TBs under unidirectional deformation11,12,17,18,19. Thus, the inclined TB could hardly strengthen materials and it is also the weakest site in the fatigued bicrystals. Therefore the fatigue performance of the materials could be improved through controlling the inclination of the TBs and it is important to prepare materials with highly textured TB. It has been documented that the TBs are normal to the growth direction during magnetron sputtering, electrodeposition or solution precipitation8,17,38. There could also be TBs of pronounced meso-texture, which appeared after cold rolling and consequent thermal treatment39. These methods enable the control over the TB orientations in real samples. However, the specimen size, the twin thickness and the texture strength of TBs need to be improved by more studies in future.

In conclusion, the fatigue cracking behaviours of the copper bicrystals with a single TB was investigated. Quite distinct from the high-angle GB, the intrinsic role of TB varies with the TB inclination angle. The fatigue cracking behaviours of the bicrystals could be controlled by adjusting the TB orientation, which provides important implications for the interfacial engineering design of materials in the future. The current work unveils the specialty of the TB with cyclic loading which would also inspire scientific research about other special GB.

Methods

Sample preparation

Bulk copper bicrystal with a coherent TB as its sole internal boundary was grown from oxygen-free high-conductivity copper of 99.999% purity by Bridgman method. The crystallographic orientation was determined by electron backscatter diffraction. The inverse pole figure and GB map of the twinned bicrystal is displayed in Fig. 1a and the colour represents the orientation along the normal direction of the bicrystal with the colour key displayed as the inset. The same colour indicates that the normal direction of the two grains are the same and near <110> direction. The same normal direction of the component grains means that the TB is vertical along the thickness direction. As shown in Fig. 1b, the {111} poles of the two grains are symmetrical about the TB plane (the white dashed line). The poles with a circle surrounding belong to the matrix grain while the rest poles represent the twin grain and the symmetric {111} poles means that it is a coherent TB. The way in which the specimens were prepared from the bulk materials is illustrated in Fig. 1a. The size of the gauge section of the specimen is about 2.5 × 2.5 × 6 mm3. All the fatigue specimens were ground and electropolished carefully before cyclic deformation.

Experimental methods

The bicrystal specimens were cyclically deformed under loading control at room temperature in air and a triangle wave with a frequency of 1 Hz was applied with an Instron E1000 testing machine. More than three specimens for each kind of bicrystal were applied in the fatigue experiments. Tests in cyclic deformation were conducted under load control. The bicrystals were fatigued with zero mean stress at increased stress amplitude. The shear stress amplitude increased stepwise from 10 MPa to about 32 MPa and after that the shear stress amplitude was kept at 32 MPa (corresponding to their cyclic saturation resolved shear stress40) with little adjustment. The total strain amplitudes reached at the final stress amplitudes of all the specimens are all calculated to be about 1% on the basis of the beam displacement detected by the testing machine. The fatigue specimens were cyclically deformed until fatigue cracks initiated either at the TBs or SBs which could be detected by the SEM. The cyclic numbers needed to detect the SB cracks are higher than 5 × 104 in the bicrystal with a parallel TB, the longest in all the fatigue specimens. For the bicrystals with the TB inclined to the loading direction, the cyclic numbers are the lowest, around 2 × 104. It is about 3 × 104 cycles at which the fatigue crack was observed in the bicrystal with a TB perpendicular to the loading direction. The resolved shear stress of the bicrystal with a perpendicular TB increased monotonously with increasing cyclic number without saturation phenomenon as that in a cyclically deformed <111> copper single crystal27,30. Thus the nominal resolved shear stress amplitude has been raised to about 48 MPa until the fatigue cracks were detected.

Slip morphology and dislocation arrangement observation

The slip morphologies and fatigue cracks of the specimens were observed by Zeiss Supra-35 SEM. After SEM observation on the surface, the specimens were ground and electropolished again and examined by ECC imaging technique3,41 to detect the dislocation arrangement near the TB. A channelling contrast is produced by using the conventional image scanning with a back-scattered electron detector. There are four quadrant-back-scattering-detectors and there is no tilt of the specimens or the incident beam. The four quadrant-back-scattering-detectors were all set as negative in this ECC observation so the ECC images are similar in appearance to the TEM bright field micrographs. The incident electron beam is along <110>, the normal direction of the specimen. Unlike the ECC observation on materials with low dislocation density42, the diffraction conditions could be relaxed in the present study in detecting the fatigued dislocation arrangements43,44,45,46. The working distance is about 8 mm and the acceleration voltage is 20 kV using an aperture of 60 μm.

Additional information

How to cite this article: Li, L. L. et al. Controllable fatigue cracking mechanisms of copper bicrystals with a coherent twin boundary. Nat. Commun. 5:3536 doi: 10.1038/ncomms4536 (2014).