Abstract
Recent experiments on p-orbital atomic bosons have suggested the emergence of a spectacular ultracold superfluid with staggered orbital currents in optical lattices. This raises fundamental questions concerning the effects of thermal fluctuations as well as possible ways of directly observing such chiral order. Here we show via Monte Carlo simulations that thermal fluctuations destroy this superfluid in an unexpected two-step process, unveiling an intermediate normal phase with spontaneously broken time-reversal symmetry, dubbed a ‘chiral Bose liquid’. For integer fillings (n≥2) in the chiral Mott regime, thermal fluctuations are captured by an effective orbital Ising model, and Onsager’s powerful exact solution is adopted to determine the transition from this intermediate liquid to the para-orbital normal phase at high temperature. A lattice quench is designed to convert the staggered angular momentum, previously thought by experts difficult to directly probe, into coherent orbital oscillations, providing a time-resolved dynamical signature of chiral order.
Similar content being viewed by others
Introduction
Orbital degrees of freedom and interactions play a crucial role in the emergence of many complex phases in solid state materials. High temperature superconductivity in the cuprates1 and pnictides2, colossal magnetoresistance observed in Mn oxides3, and chiral p-wave superconductivity proposed in Sr2RuO4 (ref. 4), are all nucleated by strong correlation effects in a multi-orbital setting5. For ultracold atomic gases, interaction effects combined with the band topology of p orbitals6 have been argued to lead to exotic topological or superfluid (SF) phases for fermions7,8,9,10,11,12,13 as well as bosons14,15,16,17,18,19,20,21,22,23,24,25. Interactions are predicted to drive a semi-metal to topological insulator quantum phase transition in two-dimensions (2D) for fermions in px, py and  orbitals12, while interacting p-orbital atomic fermions in three-dimensions (3D) could lead to axial orbital order26. For weakly interacting 2D lattice bosons in px and py orbitals the ground state is proposed to be a SF with staggered px±ipy order15; such order is also found for one-dimensional (1D) strongly interacting p-orbital bosons24. For bosons, these exotic phases can result from a particularly simple effect: repulsive contact interactions favour a maximization of the local angular momentum z, a bosonic variant of the atomic Hund’s rule for electrons15,22,25.
orbitals12, while interacting p-orbital atomic fermions in three-dimensions (3D) could lead to axial orbital order26. For weakly interacting 2D lattice bosons in px and py orbitals the ground state is proposed to be a SF with staggered px±ipy order15; such order is also found for one-dimensional (1D) strongly interacting p-orbital bosons24. For bosons, these exotic phases can result from a particularly simple effect: repulsive contact interactions favour a maximization of the local angular momentum z, a bosonic variant of the atomic Hund’s rule for electrons15,22,25.
Here we study p-orbital phases beyond their ground state properties, focusing on open fundamental issues such as thermal and dynamical effects, to be elaborated below. Our work is motivated by recent experiments that have successfully prepared long-lived metastable phases of weakly interacting 87Rb atoms in p orbitals21,27. In the deep lattice regime, this experimental system is well approximated by a tight binding model on a checkerboard optical lattice with bosons in the px, py and s orbital degrees of freedom (see Fig. 1). The Hamiltonian of the model is obtained by extending the early theoretical studies14,15,22,28 to the checkerboard lattice configuration used in the recent experiments of Wirth et al.21 and Ölschläger et al.27 Restricting ourselves to nearest-neighbor tunnelling, the Hamiltonian is H=Htun+Hloc, with tunnelling and local terms27,
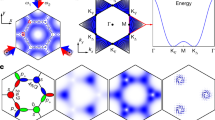
(a) The checkerboard lattice structure as used in experiments to realize p-orbital superfluid21, together with the phases of the staggered orbital ordering in chiral states. The arrows ax and ay are primitive vectors of the square lattice. The symbols (+, i, −, −i) indicate the phases of each orbital wavefunction (0,π/2,π,3π/2), respectively. (b)The schematic phase diagram of p-orbital band Bosons with filling n≥2. The topology of the phase diagram is fixed by exact or controlled numerical and analytical calculations in the strong and weak coupling limits at non-zero temperature and for arbitrary coupling along the T=0 line of ‘Chiral Mott’ and is otherwise interpolated schematically elsewhere. At zero temperature there is a quantum phase transition between the chiral MI and superfluid phases, both of which break time-reversal symmetry. At finite temperature, there is a chiral Bose liquid phase. On heating, the chiral superfluid undergoes a BKT transition into the chiral Bose liquid, which subsequently undergoes an Ising transition at a higher temperature into a normal Bose liquid.


Here, bx(x), by(x) and bs(x) are bosonic annihilation operators of px, py and s orbitals at site x. The position vectors r=rxax+ryay, with integers rx and ry. The vector ax (ay) is the primitive vector of the square lattice in the x (y) direction (Fig. 1). The positions of s orbitals are  ,
,  ,
,  and
and  . The density operators are defined as
. The density operators are defined as  and
and  . The angular momentum operator is
. The angular momentum operator is

Note that a square lattice C4 rotational symmetry has been assumed.
With an analysis of the time-of-flight momentum distribution, Wirth et al.21 and Ölschläger et al.27 found evidence suggesting a staggered px±ipy SF. However, a direct measurement of its key property—the angular momentum order—remains a challenge. This is especially crucial in the absence of SF coherence, since quantum or thermal fluctuations may kill superfluidity while preserving chiral angular momentum order. This issue is also relevant to chiral electronic fluids proposed to emerge in Sr2RuO4 (refs 29, 30, 31), doped graphene32 and the pseudogap state of high-temperature superconductors33,34,35.
While previous work has focused on the ground state properties of such unconventional Bose SFs, there remain important outstanding issues to be addressed. First, how do thermal or quantum fluctuations, which are important in any experimental setting, melt these unconventional SF states? Second, which experiment can directly detect the spatially modulated angular momentum underlying these unusual quantum states? And finally, what can one learn from the time-resolved dynamics of such complex orbital states?
This brings us to two central results responding to the above open questions. First, using classical Monte Carlo simulations of an effective model of interacting px and py bosons, we show that thermal fluctuations lead to a two-step melting of the staggered px±ipy SF ground state. Sandwiched between a lower temperature Berezinskii–Kosterlitz–Thouless (BKT) transition at which superfluidity is lost, and a higher temperature Ising transition at which time-reversal symmetry is restored, lies a ‘chiral Bose liquid’ with spontaneously broken time-reversal symmetry. In other words, it is a remarkable state of matter that is chiral but not SF. For large Hubbard repulsion at integer fillings, n≥2, a strong coupling expansion yields Mott insulating states with staggered px±ipy order. As shown schematically in Fig. 1, this opens up a wide window in the phase diagram where staggered angular momentum order persists even in the absence of superfluidity. Our work represents the first study of the finite temperature properties of staggered px±ipy chiral Bose fluids. Second, mapping the px, py orbitals onto an effective pseudospin-1/2 degree of freedom, we show that one can simulate the spin dynamics in magnetic solids by orbital dynamics of p-band bosons. Specifically, we numerically study a particular lattice quench, using time-dependent matrix product and Gutzwiller states, which is shown to convert the angular momentum order of such chiral fluids into time-dependent oscillations of the orbital population imbalance, analogous to Larmor spin precession. These oscillations directly reveal the experimentally hard-to-detect ‘hidden order’ associated with spontaneous time-reversal symmetry breaking. This quench is analogous to nuclear magnetic resonance schemes in liquids or solids, which tip the nuclear moment vector and study its subsequent precession using radio-frequency probes. This non-interferometric, and time-resolved, route to measuring the angular momentum order works in SF as well as non-SF regimes, and it could be implemented using recent experimental innovations36,37,38.
Results
Chiral Bose liquid and Mott insulator at strong coupling
We begin with the strong coupling regime, where atoms can localize to form a Mott insulator (MI) ground state. When the s orbitals in one of the sublattices (Fig. 1) are largely mismatched in energy with the p orbitals, with a gap Δsp, the nearest-neighbor tunnelling Hamiltonian for bosons dominantly residing in the p orbitals is given by

with hopping amplitudes  being mediated by the s orbitals. At integer filling, with n≥2, a strong p-orbital Hubbard repulsion in equation (2) favors a local state with a fixed particle number with non-zero angular momentum in order to minimize the interaction energy22,24,25,28, leading to a MI with a two-fold degeneracy of orbital states px±ipy at each site. This extensive degeneracy is lifted by virtual boson fluctuations within second order perturbation theory in the boson hopping amplitudes. This effect is captured, by setting z(r)=σz(r)|z(r)|, and deriving an effective exchange Hamiltonian between the Ising degrees of freedom σz(r),
being mediated by the s orbitals. At integer filling, with n≥2, a strong p-orbital Hubbard repulsion in equation (2) favors a local state with a fixed particle number with non-zero angular momentum in order to minimize the interaction energy22,24,25,28, leading to a MI with a two-fold degeneracy of orbital states px±ipy at each site. This extensive degeneracy is lifted by virtual boson fluctuations within second order perturbation theory in the boson hopping amplitudes. This effect is captured, by setting z(r)=σz(r)|z(r)|, and deriving an effective exchange Hamiltonian between the Ising degrees of freedom σz(r),

where  . The chiral MI ground state thus supports a staggered (antiferromagnetic) angular momentum pattern, with a non-zero order parameter
. The chiral MI ground state thus supports a staggered (antiferromagnetic) angular momentum pattern, with a non-zero order parameter  out to arbitrarily strong coupling. Such staggered time-reversal symmetry broken MIs, albeit for far more delicate plaquette currents, are known to emerge in frustrated Bose Hubbard models without orbital degrees of freedom, but only in an extremely small parameter window of interactions39,40,41. As schematically shown in Fig. 1, heating this MI leads to a ‘chiral Bose liquid’ with spontaneously broken time-reversal symmetry. It only reverts to a conventional normal fluid above a symmetry restoring thermal phase transition of
out to arbitrarily strong coupling. Such staggered time-reversal symmetry broken MIs, albeit for far more delicate plaquette currents, are known to emerge in frustrated Bose Hubbard models without orbital degrees of freedom, but only in an extremely small parameter window of interactions39,40,41. As schematically shown in Fig. 1, heating this MI leads to a ‘chiral Bose liquid’ with spontaneously broken time-reversal symmetry. It only reverts to a conventional normal fluid above a symmetry restoring thermal phase transition of  , which occurs at kBTI≈2.27 adopted from the exact result42. Taking
, which occurs at kBTI≈2.27 adopted from the exact result42. Taking  =0.02 and U=1 in units of the recoil energy of the optical lattice, we estimate the Ising transition temperature in the experimental system21,27 to be ~1nK, well within the reach of cooling techniques in optical lattices.
=0.02 and U=1 in units of the recoil energy of the optical lattice, we estimate the Ising transition temperature in the experimental system21,27 to be ~1nK, well within the reach of cooling techniques in optical lattices.
Monte Carlo simulations at weak coupling
At low temperature, and with decreasing interaction strength, we expect both the chiral Bose liquid and the chiral MI to become unstable to superfluidity25. Equivalently, decreasing temperature at weak coupling is expected to lead to a sequence of transitions from normal to chiral Bose liquid and subsequently to chiral SF as shown in Fig. 1b. To address this physics in the weak coupling limit, we begin with the Hamiltonian  , supplemented with local p-orbital interactions
, supplemented with local p-orbital interactions

For small  , the band structure of p-band bosons has minima at (π, 0) and (0, π). Interactions scatter boson pairs from one minimum into the other, leading the bosons to condense into a superposition state of the two modes, phase-locked with a relative phase ±π/2. This gives rise to a px±ipy SF ground state with a spontaneously broken time-reversal symmetry and non-zero staggered angular momentum order.
, the band structure of p-band bosons has minima at (π, 0) and (0, π). Interactions scatter boson pairs from one minimum into the other, leading the bosons to condense into a superposition state of the two modes, phase-locked with a relative phase ±π/2. This gives rise to a px±ipy SF ground state with a spontaneously broken time-reversal symmetry and non-zero staggered angular momentum order.
To study the impact of thermal fluctuations on this weakly correlated SF, we make the reasonable assumption that classical phase fluctuations dominate the universal physics in the vicinity of the thermal phase transitions of this SF. This allows us to ignore the subdominant density fluctuations, and to replace  , with ρ being the boson density, arriving at an effective classical phase-only Hamiltonian
, with ρ being the boson density, arriving at an effective classical phase-only Hamiltonian

where Δjθα(r)=θα(r+aj)–θα(r) with j=x, y,  and U≈ρ2Up/6. A more powerful symmetry-based effective field theory (EFT) approach (see Methods) confirms exactly the same lattice-regularized model. Using Monte Carlo simulations (see Methods), we have studied the thermal phase diagram of this model for fixed U/
and U≈ρ2Up/6. A more powerful symmetry-based effective field theory (EFT) approach (see Methods) confirms exactly the same lattice-regularized model. Using Monte Carlo simulations (see Methods), we have studied the thermal phase diagram of this model for fixed U/ , with
, with  =1.
=1.
As shown in Fig. 2a, the Binder cumulant43 BL(z) for the staggered angular momentum order, computed for U/ =1 on L × L systems with various L, exhibits a unique crossing point at T/
=1 on L × L systems with various L, exhibits a unique crossing point at T/ =2.088(3), signalling a critical point with a diverging correlation length. The critical value of this Binder cumulant is B*≈0.61, very close to the universal 2D Ising value ≈0.61069 for the aspect ratio of unity and periodic boundary conditions used in our simulations. This suggests that the staggered angular momentum order disappears at TI/
=2.088(3), signalling a critical point with a diverging correlation length. The critical value of this Binder cumulant is B*≈0.61, very close to the universal 2D Ising value ≈0.61069 for the aspect ratio of unity and periodic boundary conditions used in our simulations. This suggests that the staggered angular momentum order disappears at TI/ =2.088(3) via a thermal transition in the 2D Ising universality class. We confirm this from the scaling collapse of the order parameter curves shown in Fig. 2b using 2D Ising exponents ν=1 and β=1/8.
=2.088(3) via a thermal transition in the 2D Ising universality class. We confirm this from the scaling collapse of the order parameter curves shown in Fig. 2b using 2D Ising exponents ν=1 and β=1/8.
(a) Binder cumulant BL(z) of the staggered angular momentum order parameter for different system sizes L showing a crossing point at the Ising transition at T/ =2.088(3). The dash dotted line indicates the universal value of the critical Binder cumulant 0.61069… for a 2D Ising transition. (b) Scaling collapse of the angular momentum order parameter curves for Ising exponents ν=1 and β=1/8.
=2.088(3). The dash dotted line indicates the universal value of the critical Binder cumulant 0.61069… for a 2D Ising transition. (b) Scaling collapse of the angular momentum order parameter curves for Ising exponents ν=1 and β=1/8.
To track the destruction of superfluidity, we have computed the atom momentum distribution function  , which is accessible via time-of-flight measurements, as well as the SF stiffness ρs (see Methods). On general grounds, a 2D quasi-condensed SF is expected to lose its superfluidity via a BKT transition driven by vortex unbinding, and it has been observed in trapped ultracold atom SFs. The BKT transition is signalled by a jump in ρs satisfying the universal relation ρs(TBKT)=2TBKT/π.
, which is accessible via time-of-flight measurements, as well as the SF stiffness ρs (see Methods). On general grounds, a 2D quasi-condensed SF is expected to lose its superfluidity via a BKT transition driven by vortex unbinding, and it has been observed in trapped ultracold atom SFs. The BKT transition is signalled by a jump in ρs satisfying the universal relation ρs(TBKT)=2TBKT/π.
As seen from Fig. 3a, ρs indeed appears to have a sharp drop in the temperature range 2.05–2.10, rounded by finite size effects. To confirm the BKT nature of the SF transition, and to precisely locate TBKT, we resort to three distinct approaches. The first uses the finite-size scaling of ρs. Weber and Minnhagen44 have derived the finite-size scaling of the SF density at TBKT. An unbiased fit to this log-scaling form (see Methods) shows that the fit error (Fig. 3c) exhibits the expected deep minimum at the BKT transition, enabling us to estimate TBKT/ =2.072(3), and ρs(TBKT)/TBKT≈0.64. The latter is close to the universal value 2/π=0.6366…, providing further concrete evidence of a BKT transition. The second uses finite-size scaling of the transition temperature. We identify the finite-size BKT transition temperature Tc(L) via ρs(Tc(L),L)=2Tc(L)/π. Above a BKT transition, the correlation length
=2.072(3), and ρs(TBKT)/TBKT≈0.64. The latter is close to the universal value 2/π=0.6366…, providing further concrete evidence of a BKT transition. The second uses finite-size scaling of the transition temperature. We identify the finite-size BKT transition temperature Tc(L) via ρs(Tc(L),L)=2Tc(L)/π. Above a BKT transition, the correlation length  , yielding a finite-size scaling form
, yielding a finite-size scaling form  (σ and L0 are non-universal numbers). An extrapolation using this formula, as shown in Fig. 3b,d, yields TBKT/
(σ and L0 are non-universal numbers). An extrapolation using this formula, as shown in Fig. 3b,d, yields TBKT/ =2.065(4). The third uses the momentum distribution n(k). As shown in Fig. 3e, n(k) exhibits equal height peaks at k1=(π, 0) and k2=(0, π). This is consistent with the weak coupling analysis, which shows degenerate p-band dispersion minima at these momenta. At a BKT transition, n(ki)∝L7/4 (in contrast to scaling as ρcL2 for a true Bose condensate with a condensate density ρc). This implies that the scaled momentum distribution n(ki)L−7/4 should cross at TBKT for varying system sizes L. The plot of this scaled distribution (Fig. 3f) indeed reveals a unique crossing point, which yields TBKT/
=2.065(4). The third uses the momentum distribution n(k). As shown in Fig. 3e, n(k) exhibits equal height peaks at k1=(π, 0) and k2=(0, π). This is consistent with the weak coupling analysis, which shows degenerate p-band dispersion minima at these momenta. At a BKT transition, n(ki)∝L7/4 (in contrast to scaling as ρcL2 for a true Bose condensate with a condensate density ρc). This implies that the scaled momentum distribution n(ki)L−7/4 should cross at TBKT for varying system sizes L. The plot of this scaled distribution (Fig. 3f) indeed reveals a unique crossing point, which yields TBKT/ ≈2.067(3).
≈2.067(3).
(a) The superfluid stiffness ρs plotted over a wide range of temperature showing a rapid drop consistent with finite size effects at a BKT transition. (b) ρs for a wide range of system sizes near the transition. (c) The r.m.s. error from fitting ρs(L) to the Weber–Minnhagen log-scaling form at different temperatures with a steep minimum at the BKT transition point T/ =2.072(3). The dash dotted line in (b) shows 2T/π and its crossing with the curves ρs(T) defines finite size BKT transition temperatures, obeying a scaling relation Tc(L)=TBKT+σ/ln2(L/L0) (see text). The extrapolation of Tc(L) to the thermodynamic limit shown in (d) predicts TBKT/
=2.072(3). The dash dotted line in (b) shows 2T/π and its crossing with the curves ρs(T) defines finite size BKT transition temperatures, obeying a scaling relation Tc(L)=TBKT+σ/ln2(L/L0) (see text). The extrapolation of Tc(L) to the thermodynamic limit shown in (d) predicts TBKT/ =2.065(4). (e) Momentum distribution over the Brillouin zone, with equal height peaks at k1≡(π,0) and k2≡(0,π). (f) Scaled momentum distribution n(k1)L−7/4 for different system sizes L, showing a crossing at 2.067(3), the BKT transition point. Also shown is the Ising transition temperature determined previously from the Binder cumulant analysis. Stated error bars on the transition points include statistical as well as extrapolation errors where applicable.
=2.065(4). (e) Momentum distribution over the Brillouin zone, with equal height peaks at k1≡(π,0) and k2≡(0,π). (f) Scaled momentum distribution n(k1)L−7/4 for different system sizes L, showing a crossing at 2.067(3), the BKT transition point. Also shown is the Ising transition temperature determined previously from the Binder cumulant analysis. Stated error bars on the transition points include statistical as well as extrapolation errors where applicable.
All three methods to locate TBKT yield consistent answers. Combining these results, our best estimate for the SF transition temperature is TBKT/ ≈2.069(4). For
≈2.069(4). For  =U=0.3, in units of recoil energy of the experimental optical lattice21,27, we estimate TBKT~50 nK. Our numerical study unambiguously shows that the chiral px±ipy SF undergoes a two-step destruction: a lower temperature BKT transition at which superfluidity is lost, followed by a higher temperature Ising transition at which time-reversal symmetry is restored, leading to an unconventional ‘chiral Bose liquid’ at intermediate temperatures 2.069(4)≲T/
=U=0.3, in units of recoil energy of the experimental optical lattice21,27, we estimate TBKT~50 nK. Our numerical study unambiguously shows that the chiral px±ipy SF undergoes a two-step destruction: a lower temperature BKT transition at which superfluidity is lost, followed by a higher temperature Ising transition at which time-reversal symmetry is restored, leading to an unconventional ‘chiral Bose liquid’ at intermediate temperatures 2.069(4)≲T/ ≲2.088(3). Such multiple transitions are also proposed to be relevant for 2D spinor condensates45. With increasing correlations, the BKT transition temperature is expected to get suppressed, eventually vanishing at the Mott transition (for integer fillings n≥2), while the Ising transition remains non-zero for arbitrarily large repulsion as seen from our strong coupling results. Correlation effects thus enhance the window where one realizes a ‘chiral Bose liquid’ as shown in the schematic temperature-interaction phase diagram in Fig. 1.
≲2.088(3). Such multiple transitions are also proposed to be relevant for 2D spinor condensates45. With increasing correlations, the BKT transition temperature is expected to get suppressed, eventually vanishing at the Mott transition (for integer fillings n≥2), while the Ising transition remains non-zero for arbitrarily large repulsion as seen from our strong coupling results. Correlation effects thus enhance the window where one realizes a ‘chiral Bose liquid’ as shown in the schematic temperature-interaction phase diagram in Fig. 1.
Quantum quench and single-site orbital dynamics
One can draw a fruitful analogy between the two orbital states at each site px, py and a pseudospin-1/2 degree of freedom ↑,↓. This suggests that one can simulate spin dynamics in solid state materials by studying orbital dynamics of p-band bosons. As we will see, this also suggests a route to directly detecting the angular momentum order in the px±ipy SF and ‘chiral Bose liquid’ of the type we have obtained. In our analogy, the px±ipy state corresponds to a pseudospin pointing along the y direction in spin space. Applying a ‘magnetic field’ along the x direction to this pseudospin should then induce Larmor precession, leading to periodic oscillations of the z-magnetization, corresponding to oscillations in the orbital population imbalance N(px)–N(py). Let us imagine we prepare the system in a certain initial state, and then suddenly quench to a state where we set Up=Us=0, turn off all hoppings so t=0, and turn on a ‘magnetic field’ term

at time τ=0; we later discuss how to realize such a term in optical lattice experiments. The staggered sign  leads to a staggered coupling between the px and py orbitals. If initially a staggered superposition px±eiθpy is prepared, this results in a rectification of all local Larmor precessions such that they add up to produce a macroscopic oscillation of the populations of the px and py orbitals. The p-orbital imbalance,
leads to a staggered coupling between the px and py orbitals. If initially a staggered superposition px±eiθpy is prepared, this results in a rectification of all local Larmor precessions such that they add up to produce a macroscopic oscillation of the populations of the px and py orbitals. The p-orbital imbalance,  , evolves, within a Heisenberg picture, as
, evolves, within a Heisenberg picture, as

where  is the staggered angular momentum operator whose evolution is in turn given by
is the staggered angular momentum operator whose evolution is in turn given by

This leads to periodic oscillations of ΔN(r,τ)=‹ΔN(r,τ)› as

where ΔN(r, 0) and  (r, 0) denote the initial orbital magnetization and staggered angular momentum, respectively. Neglecting possible spatial inhomogeneity in λ(r) and φ(r), by focusing at the trap centre, we can set λ(r)=λ and φ(r)=φ, and extract the initial angular momentum order from the amplitude A(r) and the phase shift φ in the dynamics of the averaged number difference
(r, 0) denote the initial orbital magnetization and staggered angular momentum, respectively. Neglecting possible spatial inhomogeneity in λ(r) and φ(r), by focusing at the trap centre, we can set λ(r)=λ and φ(r)=φ, and extract the initial angular momentum order from the amplitude A(r) and the phase shift φ in the dynamics of the averaged number difference  with Ns being the number of lattice sites at the trap centre, and
with Ns being the number of lattice sites at the trap centre, and  denoting the spatial average of (…). The coefficient λ can be directly read-off from the oscillation period τQ ≡ π/λ. We emphasize here that
denoting the spatial average of (…). The coefficient λ can be directly read-off from the oscillation period τQ ≡ π/λ. We emphasize here that  suitably averaged over the entire trap can be measured in time-of-flight experiments21.
suitably averaged over the entire trap can be measured in time-of-flight experiments21.
For a state with non-zero staggered angular momentum order, but no initial orbital population imbalance, that is, ΔN(r,0)=0, such as our chiral fluids, we expect  (τ) to oscillate with a non-zero amplitude, and a phase shift φ=±π/2 whose sign will fluctuate from realization to realization, reflecting the spontaneous nature of time-reversal symmetry breaking. The amplitude of the signal will then be a direct measure of the staggered angular momentum order parameter, vanishing in a singular manner at the Ising phase transition, which restores time-reversal symmetry. In contrast, a completely thermally disordered conventional normal fluid would have
(τ) to oscillate with a non-zero amplitude, and a phase shift φ=±π/2 whose sign will fluctuate from realization to realization, reflecting the spontaneous nature of time-reversal symmetry breaking. The amplitude of the signal will then be a direct measure of the staggered angular momentum order parameter, vanishing in a singular manner at the Ising phase transition, which restores time-reversal symmetry. In contrast, a completely thermally disordered conventional normal fluid would have  (τ)=0. A state with an initial orbital population imbalance but no angular momentum order, obtained by explicitly breaking the square lattice C4 symmetry in the initial Hamiltonian as achieved in recent experiments, would exhibit oscillations with a nonsingular amplitude and a phase shift φ=0. Finally, if spontaneous time-reversal symmetry breaking exists in a system without C4 symmetry, the amplitude of
(τ)=0. A state with an initial orbital population imbalance but no angular momentum order, obtained by explicitly breaking the square lattice C4 symmetry in the initial Hamiltonian as achieved in recent experiments, would exhibit oscillations with a nonsingular amplitude and a phase shift φ=0. Finally, if spontaneous time-reversal symmetry breaking exists in a system without C4 symmetry, the amplitude of  (τ) will be nonsingular while its phase shift will change in a singular manner, going from φ=±π/2 in a completely ordered state to φ=0 at the time-reversal symmetry restoring phase transition. Since this quench induced orbital magnetization dynamics is inherently a non-interferometric probe of the angular momentum order, it suggests a simple and powerful method for measuring time-reversal symmetry breaking in SF as well as non-SF chiral states. Our proposal thus significantly extends the earlier proposed quench dynamics approach for probing generic current orders46,47. In the presence of SF order, our real space quench is analogous to the recent proposal of Cai et al.48, which proposes to extract the relative phase between the px and py orbitals by studying momentum spectra after applying a Raman pulse to the Bose condensate. However, our proposal differs in showing that the angular momentum order can be probed irrespective of long range phase coherence or sharp momentum peaks.
(τ) will be nonsingular while its phase shift will change in a singular manner, going from φ=±π/2 in a completely ordered state to φ=0 at the time-reversal symmetry restoring phase transition. Since this quench induced orbital magnetization dynamics is inherently a non-interferometric probe of the angular momentum order, it suggests a simple and powerful method for measuring time-reversal symmetry breaking in SF as well as non-SF chiral states. Our proposal thus significantly extends the earlier proposed quench dynamics approach for probing generic current orders46,47. In the presence of SF order, our real space quench is analogous to the recent proposal of Cai et al.48, which proposes to extract the relative phase between the px and py orbitals by studying momentum spectra after applying a Raman pulse to the Bose condensate. However, our proposal differs in showing that the angular momentum order can be probed irrespective of long range phase coherence or sharp momentum peaks.
Numerical simulations of quench dynamics
Our above analysis assumed that the quantum quench was complete, that is, all tunnelings (t) and interactions (U) were entirely switched off when Hmag was switched on. We now show, using numerical simulations, that the coherent orbital oscillations are robust even with small non-zero tunnelings and interactions present after the quench, that is, for an incomplete quench.
Since the scheme we are proposing here directly measures the local angular momentum order, it does not rely on the system dimensionality (beyond the assumption of long-range order). We therefore numerically simulate the zero temperature quench dynamics of a 1D model of p-orbital bosons, using both time-dependent Gutzwiller mean field theory49 and time-dependent matrix product states (tMPS), finding good agreement at both weak and strong couplings and qualitatively similar conclusions at intermediate interaction strength. We then use the Gutzwiller mean field theory to also simulate the dynamics for the 2D case relevant to current experiments.
The Hamiltonian of the 1D system is24

where j index lattice sites. The ground state phase diagram of this 1D system includes two types of Mott states at strong coupling: a chiral Mott with staggered angular momentum order, and a non-chiral MI. For weak correlations, it supports two types of SF ground states: a chiral SF with staggered angular momentum order and a non-chiral SF24. The chiral states have an order parameter  , with
, with  , which is analogous to the 2D case. We start with different ground states of H1D and study their time evolution under a quantum quench that suddenly changes the Hamiltonian to H1D+ΔH1D, where
, which is analogous to the 2D case. We start with different ground states of H1D and study their time evolution under a quantum quench that suddenly changes the Hamiltonian to H1D+ΔH1D, where

The oscillatory dynamics of  and
and  is confirmed even for these entangled many-body states (Fig. 4). Since the 1D geometry does not possess C4 symmetry, we expect the different states to be distinguished by the phase shift φ, not the amplitude, of the oscillatory dynamics. The chiral Mott and SF states develop a periodic motion with non-zero phase shift. The dynamics of non-chiral states indicate zero phase shift. In this way the chiral states can be distinguished from non-chiral states by measuring the phase shift, which is directly related to the angular momentum order parameter. Deep in the chiral SF state, the phase shift is φ=±π/2, and it decreases in magnitude on approaching the chiral–non-chiral critical point. The phase shift vanishes in a singular fashion at this quantum critical point, signalling that this phase transition associated with time-reversal symmetry can be probed by measuring the order parameter via the phase shift φ.
is confirmed even for these entangled many-body states (Fig. 4). Since the 1D geometry does not possess C4 symmetry, we expect the different states to be distinguished by the phase shift φ, not the amplitude, of the oscillatory dynamics. The chiral Mott and SF states develop a periodic motion with non-zero phase shift. The dynamics of non-chiral states indicate zero phase shift. In this way the chiral states can be distinguished from non-chiral states by measuring the phase shift, which is directly related to the angular momentum order parameter. Deep in the chiral SF state, the phase shift is φ=±π/2, and it decreases in magnitude on approaching the chiral–non-chiral critical point. The phase shift vanishes in a singular fashion at this quantum critical point, signalling that this phase transition associated with time-reversal symmetry can be probed by measuring the order parameter via the phase shift φ.
Dots and lines are results of tMPS and Gutzwiller methods, respectively. The upper (bottom) panel shows dynamics of Mott (superfluid) states. In the upper panel the dash dotted line with circles and the solid line with diamonds correspond to chiral (two particles per site) and non-chiral (one particle per site) Mott states, respectively. In the bottom panel, the dash dotted line with circles and the dashed line with squares correspond to two chiral superfluid states with filling at 1.5 and 2, respectively; the solid line with diamonds is for a non-chiral superfluid state with filling at 0.5. For the chiral superfluid state with filling at 2,  =U/3=λ/10 is used, and for the other states
=U/3=λ/10 is used, and for the other states  =0.045U=0.09λ is used. The time unit τQ is π/λ.
=0.045U=0.09λ is used. The time unit τQ is π/λ.
Comparing time-dependent Gutzwiller50 and tMPS methods (Fig. 4), we find that the Gutzwiller approach captures orbital dynamics fairly well. We thus apply this approach to study orbital dynamics of the 2D system, as in experiments21. We have verified that a partial quench leads to long-lived ΔN oscillations as long as t and U are weak compared with the quench strength, that is,  and
and  . These results are shown in Fig. 5.
. These results are shown in Fig. 5.
Experimental proposal for quench
To engineer the Hamiltonian Hmag of Equation (8), we implement a quench potential Vmag(x) modulated in the (1,1) direction in addition to the lattice potential giving rise to the quench Hamiltonian

with

which is valid in the tight binding regime when the quench potential is weak as compared with the original optical lattice (see Supplementary Note 1). Here, ω0 is the harmonic oscillator frequency of the lattice wells hosting the p orbitals, and a≡|ax|=|ay| is the lattice constant. Since the local density operator of the p orbitals np(r) commutes with ΔN(r) and  , it does not contribute to the dynamics of ΔN(r), and hence may be neglected. This is verified in our Gutzwiller simulations. We choose the quench potential as
, it does not contribute to the dynamics of ΔN(r), and hence may be neglected. This is verified in our Gutzwiller simulations. We choose the quench potential as

with some integer ν≥0, a positive amplitude Γ, and Kx, Ky denoting the primitive vectors of the reciprocal lattice (ai·Kj=2πδij with i,jε{x,y}). The quench potential provides a lattice along the (1,1) direction, and it breaks both C4 symmetry and mirror symmetries in the x and y directions. The potential is minimal at every second site of the Bravais lattice at positions r(=rxax+ryay) with even rx+ry and it is maximal for all adjacent sites specified by odd rx+ry. Hence, the second derivative in Equation (15) produces the alternating sign  required for realization of the quench Hamiltonian in Equation (8). Combining Equations (16) and (15) yields
required for realization of the quench Hamiltonian in Equation (8). Combining Equations (16) and (15) yields

with Erec≡ħ2k2/2m denoting the single photon recoil energy for photons with wave number  .
.
The lattice potential together with the corresponding quench potential can be realized by superlattice techniques demonstrated in several experiments20,21,36,51. For example, following Wirth et al.21, the lattice potential arises via two optical standing waves oriented along the (1,1) and (1,−1) axes with a wave number  =2π/1,064 nm. The corresponding quench lattice requires an additional standing wave along the (1,1) axis with wave number
=2π/1,064 nm. The corresponding quench lattice requires an additional standing wave along the (1,1) axis with wave number  . Hence, the case ν=1 requires
. Hence, the case ν=1 requires  ≈2π/709 nm, which is experimentally readily provided by diode laser sources. Both standing waves along the (1, 1)-direction may be derived by retro-reflecting two parallelly propagating laser beams with wave numbers k and k′ by the same mirror. To prepare the required spatial relative phase of the two lattices, k′ may be slightly detuned from the precise ratio k′/k=
≈2π/709 nm, which is experimentally readily provided by diode laser sources. Both standing waves along the (1, 1)-direction may be derived by retro-reflecting two parallelly propagating laser beams with wave numbers k and k′ by the same mirror. To prepare the required spatial relative phase of the two lattices, k′ may be slightly detuned from the precise ratio k′/k=
Discussion
In most cold atom experiments, the trap potential can induce a slowly varying inhomogeneity in the ‘magnetic field’ λ as δλ=max{λ(r)}–min{λ(r)}. We expect the oscillations of the trap averaged number difference  to decay over a time-scale
to decay over a time-scale  . Finally we emphasize that besides the angular momentum order parameter, the quantum quench proposal and a subsequent study of ΔN(r, τ) using in-situ microscopy can also yield correlation functions of
. Finally we emphasize that besides the angular momentum order parameter, the quantum quench proposal and a subsequent study of ΔN(r, τ) using in-situ microscopy can also yield correlation functions of  (r), from which the diverging correlation length near the transition from chiral Bose liquid to normal can be extracted.
(r), from which the diverging correlation length near the transition from chiral Bose liquid to normal can be extracted.
Methods
Monte Carlo simulations
We carry out the Monte Carlo study of the Hamiltonian  in Equation (7) using a Metropolis sampling of the phase configurations {θx(r), θy(r)}, with 107 sweeps to equilibrate the system at each temperature, and averaging all observables over 108 configurations.
in Equation (7) using a Metropolis sampling of the phase configurations {θx(r), θy(r)}, with 107 sweeps to equilibrate the system at each temperature, and averaging all observables over 108 configurations.
To study the chiral order, we construct the angular momentum order parameter  and compute its Binder cumulant43
and compute its Binder cumulant43  . The universal order parameter distribution at renormalization group fixed points leads to universal values of L→∞; on finite size systems, this yields Binder cumulant curves, which cross at the critical point associated with angular momentum ordering. The critical value B* of the Binder cumulant is well-known to be universal, independent of lattice structure and details of the Hamiltonian, and depending only on the aspect ratio and boundary conditions used in the simulations. For periodic boundary conditions on L × L lattices, B*≈0.61069 for the 2D Ising universality class.
. The universal order parameter distribution at renormalization group fixed points leads to universal values of L→∞; on finite size systems, this yields Binder cumulant curves, which cross at the critical point associated with angular momentum ordering. The critical value B* of the Binder cumulant is well-known to be universal, independent of lattice structure and details of the Hamiltonian, and depending only on the aspect ratio and boundary conditions used in the simulations. For periodic boundary conditions on L × L lattices, B*≈0.61069 for the 2D Ising universality class.
The SF stiffness ρs is defined as the change in the free energy density in response to a boundary condition twist; for  , it is explicitly given by
, it is explicitly given by



where ‹⋯› refers to the thermal average. At a BKT transition, ρs(T) jumps to zero, with ρs(TBKT)/TBKT=2/π, a universal value. On finite size systems, the universal SF stiffness jump gets severely rounded, and a careful finite-size scaling is required to extract TBKT. On the basis of the KT renormalization group equations, Weber and Minnhagen have shown44 that ρs(TBKT, L) scales as

where c is a non-universal number. It is well-known that fitting to this log-scaling form at different temperatures leads to an error, which exhibits a steep minimum at TBKT, enabling us to extract TBKT from our simulations. An unbiased fit to ρs(T)/T, using a two-parameter scaling form,

further confirms the universal jump at the TBKT identified by the error minimum. Using this, we find k≈0.64 from our simulations, in very good agreement with the KT value 2/π=0.6366....
Effective field theory description
We now show that the Monte Carlo study in the Results section is a lattice model simulation of the EFT for weakly interacting bosons in the experiments21, which does not rely on tight binding approximation. In the band structure calculation for the lattice rotation symmetric case21, dispersion of the relevant p-band Ep(k) has two degenerate minima at Qx=(π,0) and Qy=(0,π), around which low energy modes can be excited due to quantum and thermal fluctuations. This leads to a two-component EFT, where the fields are introduced as

with Λ a momentum cut-off and  annihilation operators for the Bloch modes near the band minima. The form of EFT is determined by considering lattice rotation and reflection symmetries, under which the fields φα transform as
annihilation operators for the Bloch modes near the band minima. The form of EFT is determined by considering lattice rotation and reflection symmetries, under which the fields φα transform as

and

respectively. The Hamiltonian density of the EFT consistent with these symmetries is

with effective couplings  ,
,  and g’s. At tree level, they are approximated as
and g’s. At tree level, they are approximated as  ,
,  and
and



where as is the 3D scattering length, a is the lattice constant, is the periodic Bloch wavefunction, and the integral ∫d3x is over one unit cell. Details of calculation for the coupling constants are provided in the Supplementary Note 2. Although the connection of the EFT to microscopic origins is made clear in the tree level estimate, the form of EFT resulting from symmetry analysis does not rely on this estimate. In the vicinity of thermal phase transitions of the SF phases, classical phase fluctuations are expected to dominate the universal physics, which allows us to ignore the subdominant density fluctuations and to replace φα by  with ρ the total density. In terms of phases θα, the Hamiltonian density is rewritten as
with ρ the total density. In terms of phases θα, the Hamiltonian density is rewritten as

Bearing in mind the periodic nature of the phases θα, a proper lattice regularization of this EFT leads precisely to Equation (7).
Additional information
How to cite this article: Li, X. et al. Proposed formation and dynamical signature of a chiral Bose liquid in an optical lattice. Nat. Commun. 5:3205 doi: 10.1038/ncomms4205 (2014).
References
Bednorz, J. & Müller, K. Possible high Tc superconductivity in the Ba-La-Cu-O system. Zeitschrift für Physik B Condensed Matter 64, 189–193 (1986).
Kamihara, Y. et al. Iron-based layered superconductor: LaOFeP. J. Am. Chem. Soc. 128, 10012–10013 (2006).
von Helmolt, R., Wecker, J., Holzapfel, B., Schultz, L. & Samwer, K. Giant negative magnetoresistance in perovskitelike La2/3Ba1/3MnOx ferromagnetic films. Phys. Rev. Lett. 71, 2331–2333 (1993).
Luke, G. M. et al. Time-reversal symmetry-breaking superconductivity in Sr2RuO4 . Nature 394, 558–561 (1998).
Tokura, Y. & Nagaosa, N. Orbital physics in transition-metal oxides. Science 288, 462–468 (2000).
Lewenstein, M. A. & Liu, W. V. Optical lattices: orbital dance. Nat. Phys. 7, 101–103 (2011).
Zhao, E. & Liu, W. V. Orbital order in mott insulators of spinless p-band fermions. Phys. Rev. Lett. 100, 160403 (2008).
Zhang, Z., Hung, H.-H., Ho, C. M., Zhao, E. & Liu, W. V. Modulated pair condensate of p-orbital ultracold fermions. Phys. Rev. A 82, 033610 (2010).
Cai, Z., Wang, Y. & Wu, C. Stable Fulde-Ferrell-Larkin-Ovchinnikov pairing states in two-dimensional and three-dimensional optical lattices. Phys. Rev. A 83, 063621 (2011).
Hung, H.-H., Lee, W.-C. & Wu, C. Frustrated Cooper pairing and f-wave supersolidity in cold-atom optical lattices. Phys. Rev. B 83, 144506 (2011).
Zhang, Z., Li, X. & Liu, W. V. Stripe, checkerboard, and liquid-crystal ordering from anisotropic p-orbital fermi surfaces in optical lattices. Phys. Rev. A 85, 053606 (2012).
Sun, K., Liu, W. V., Hemmerich, A. & Das Sarma, S. Topological semimetal in a fermionic optical lattice. Nat. Phys. 8, 67–70 (2012).
Li, X., Zhao, E. & Liu, W. V. Topological states in a ladder-like optical lattice containing ultracold atoms in higher orbital bands. Nat. Commun. 4, 1523 (2013).
Isacsson, A. & Girvin, S. M. Multiflavor bosonic hubbard models in the first excited bloch band of an optical lattice. Phys. Rev. A 72, 053604 (2005).
Liu, W. V. & Wu, C. Atomic matter of nonzero-momentum Bose-Einstein condensation and orbital current order. Phys. Rev. A 74, 013607 (2006).
Kuklov, A. B. Unconventional strongly interacting Bose-Einstein condensates in optical lattices. Phys. Rev. Lett. 97, 110405 (2006).
Lim, L.-K., Smith, C. M. & Hemmerich, A. Staggered-vortex superfluid of ultracold bosons in an optical lattice. Phys. Rev. Lett. 100, 130402 (2008).
Stojanović, V. M., Wu, C., Liu, W. V. & Das Sarma, S. Incommensurate superfluidity of bosons in a double-well optical lattice. Phys. Rev. Lett. 101, 125301 (2008).
Zhou, Q., Porto, J. V. & Das Sarma, S. Condensates induced by interband coupling in a double-well lattice. Phys. Rev. B 83, 195106 (2011).
Soltan-Panahi, P., Lühmann, D.-S., Struck, J., Windpassinger, P. & Sengstock, K. Quantum phase transition to unconventional multi-orbital superfluidity in optical lattices. Nat. Phys. 8, 71–75 (2012).
Wirth, G., Ölschläger, M. & Hemmerich, A. Evidence for orbital superfluidity in the p-band of bipartite optical square lattice. Nat. Phys. 7, 147–153 (2011).
Li, X., Zhao, E. & Liu, W. V. Effective action approach to the p-band mott insulator and superfluid transition. Phys. Rev. A 83, 063626 (2011).
Cai, Z. & Wu, C. Complex and real unconventional Bose-Einstein condensations in high orbital bands. Phys. Rev. A 84, 033635 (2011).
Li, X., Zhang, Z. & Liu, W. V. Time-reversal symmetry breaking of p-orbital bosons in a one-dimensional optical lattice. Phys. Rev. Lett. 108, 175302 (2012).
Hébert, F. et al. Exotic phases of interacting p-band bosons. Phys. Rev. B 87, 224505 (2013).
Hauke, P. et al. Orbital order of spinless fermions near an optical feshbach resonance. Phys. Rev. A 84, 051603 (2011).
Ölschläger, M. et al. Interaction-induced chiral px±ipy superfluid order of bosons in an optical lattice. New J. Phys. 15, 083041 (2013).
Wu, C. Unconventional Bose-Einstein condensations beyond the ‘no node’ theorem. Mod. Phys. Lett. B 23, 1–24 (2009).
Mackenzie, A. P. & Maeno, Y. The superconductivity of Sr2RuO4 and the physics of spin-triplet pairing. Rev. Mod. Phys. 75, 657–712 (2003).
Kallin, C. Chiral p-wave order in Sr2RuO4 . Rep. Prog. Phys. 75, 042501 (2012).
Nandkishore, R. Prediction and description of a chiral pseudogap phase. Phys. Rev. B 86, 045101 (2012).
Nandkishore, R., Levitov, L. S. & Chubukov, A. V. Chiral superconductivity from repulsive interactions in doped graphene. Nat. Phys. 8, 158–163 (2012).
Varma, C. M. Proposal for an experiment to test a theory of high-temperature superconductors. Phys. Rev. B 61, R3804–R3807 (2000).
Chakravarty, S., Laughlin, R. B., Morr, D. K. & Nayak, C. Hidden order in the cuprates. Phys. Rev. B 63, 094503 (2001).
Fauqué, B. et al. Magnetic order in the pseudogap phase of high-Tc superconductors. Phys. Rev. Lett. 96, 197001 (2006).
Folling, S. et al. Direct observation of second-order atom tunnelling. Nature 448, 1029–1032 (2007).
Tarruell, L., Greif, D., Uehlinger, T., Jotzu, G. & Esslinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 483, 302–305 (2012).
Ölschläger, M., Wirth, G., Kock, T. & Hemmerich, A. Topologically induced avoided band crossing in an optical checkerboard lattice. Phys. Rev. Lett. 108, 075302 (2012).
Dhar, A. et al. Bose-hubbard model in a strong effective magnetic field: Emergence of a chiral mott insulator ground state. Phys. Rev. A 85, 041602 (2012).
Dhar, A. et al. Chiral mott insulator with staggered loop currents in the fully frustrated Bose-Hubbard model. Phys. Rev. B 87, 174501 (2013).
Zaletel, M. P., Parameswaran, S. A., Rüegg, A. & Altman, E. Chiral Bosonic Mott Insulator on the Frustrated Triangular Lattice. Preprint at http://arxiv.org/abs/1308.3237 (2013).
Onsager, L. Crystal statistics. i. a two-dimensional model with an order-disorder transition. Phys. Rev. 65, 117–149 (1944).
Binder, K. Finite size scaling analysis of Ising model block distribution functions. Zeitschrift für Physik B Condensed Matter 43, 119–140 (1981).
Weber, H. & Minnhagen, P. Monte carlo determination of the critical temperature for the two-dimensional XY model. Phys. Rev. B 37, 5986–5989 (1988).
Mukerjee, S., Xu, C. & Moore, J. E. Topological defects and the superfluid transition of the s=1 spinor condensate in two dimensions. Phys. Rev. Lett. 97, 120406 (2006).
Killi, M. & Paramekanti, A. Use of quantum quenches to probe the equilibrium current patterns of ultracold atoms in an optical lattice. Phys. Rev. A 85, 061606 (2012).
Killi, M., Trotzky, S. & Paramekanti, A. Anisotropic quantum quench in the presence of frustration or background gauge fields: a probe of bulk currents and topological chiral edge modes. Phys. Rev. A 86, 063632 (2012).
Cai, Z., Duan, L.-M. & Wu, C. Phase-sensitive detection for unconventional Bose-Einstein condensation. Phys. Rev. A 86, 051601 (2012).
Seibold, G. & Lorenzana, J. Time-dependent Gutzwiller approximation for the Hubbard model. Phys. Rev. Lett. 86, 2605–2608 (2001).
Snoek, M. & Hofstetter, W. Two-dimensional dynamics of ultracold atoms in optical lattices. Phys. Rev. A 76, 051603 (2007).
Anderlini, M. et al. Controlled exchange interaction between pairs of neutral atoms in an optical lattice. Nature 448, 452–456 (2007).
Acknowledgements
We acknowledge helpful discussions with Youjin Deng, Subroto Mukerjee and Sankar Das Sarma. This work is supported by the NSERC of Canada (AP), NSF PHY11-25915 (X.L.), AFOSR (FA9550-12-1-0079), ARO (W911NF-11-1-0230), DARPA OLE Program through ARO and the Charles E. Kaufman Foundation of The Pittsburgh Foundation (X.L. and W.V.L.), the National Basic Research Program of China (Grant No 2012CB922101) and Overseas Collaboration Program of NSF of China (11128407) (W.V.L.), and the German Research Foundation DFG-SFB 925 and the Hamburg Centre for Ultrafast Imaging (A.H.). X.L. would like to thank KITP at UCSB for hospitality. W.V.L. and A.H. acknowledge partial support by NSF-PHYS-1066293 and the hospitality of the Aspen Center for Physics.
Author information
Authors and Affiliations
Contributions
X.L. and A.P. conceived and evolved the theoretical ideas in discussion with W.V.L. A.H. examined and improved the experimental protocol. X.L. and A.P. performed numerical simulations. All authors worked on theoretical analysis and contributed in completing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Notes 1-2 (PDF 195 kb)
Rights and permissions
About this article
Cite this article
Li, X., Paramekanti, A., Hemmerich, A. et al. Proposed formation and dynamical signature of a chiral Bose liquid in an optical lattice. Nat Commun 5, 3205 (2014). https://doi.org/10.1038/ncomms4205
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms4205
This article is cited by
-
Chiral magnetism and spontaneous spin Hall effect of interacting Bose superfluids
Nature Communications (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

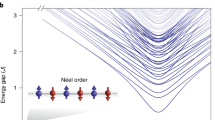





 =0.0125Up) and superfluid states (
=0.0125Up) and superfluid states ( =Up), respectively. The filling is ‹n(r)›=2. The time unit τQ is π/λ. Non-chiral phases (not shown) have ΔN=0, and do not exhibit any post-quench oscillations.
=Up), respectively. The filling is ‹n(r)›=2. The time unit τQ is π/λ. Non-chiral phases (not shown) have ΔN=0, and do not exhibit any post-quench oscillations.