Abstract
The Rashba effect is an interaction between the spin and the momentum of electrons induced by the spin-orbit coupling (SOC) in surface or interface states. Its potential for conversion between charge and spin currents has been theoretically predicted but never clearly demonstrated for surfaces or interfaces of metals. Here we present experiments evidencing a large spin-charge conversion by the Bi/Ag Rashba interface. We use spin pumping to inject a spin current from a NiFe layer into a Bi/Ag bilayer and we detect the resulting charge current. As the charge signal is much smaller (negligible) with only Bi (only Ag), the spin-to-charge conversion can be unambiguously ascribed to the Rashba coupling at the Bi/Ag interface. This result demonstrates that the Rashba effect at interfaces can be used for efficient charge-spin conversion in spintronics.
Similar content being viewed by others
Introduction
Classical spintronics1 is based on the generation of spin-polarized currents by using the exchange interaction between conduction electrons and local spins in magnetic conductors. Alternatively, as it has progressively been understood in the last decade, spin-polarized currents can also be generated (or detected) in nonmagnetic materials by the spin-orbit interactions, mainly through the Spin Hall and Rashba effects2. The spin-orbit coupling (SOC) can also be used to obtain novel types of magnetic configurations—skyrmions for example—or to induce the interesting surface or edge electronic properties of the topological insulators2. Nowadays, the studies of all these spin-orbit effects form a fast developing broad field of research that can be called spin-orbitronics.
The Spin Hall Effect (SHE), theoretically predicted long time ago3, has been experimentally investigated very actively in the last decade, first by magneto-optical measurements4 and then in transport experiments5. The SHE can be used to convert a charge current flowing in a nonmagnetic conductor into spin accumulations on the edges of the conductor, and consequently into a transverse spin current. When the SHE is large, in heavy metals or alloys having a large SOC, the spin current induced by SHE can be used to switch efficiently the magnetization of a nanomagnet or to move a magnetic domain wall6,7,8.
The Rashba effect9 comes from the influence of the SOC on the two-dimensional (2D) electron gas (2DEG) that exists at surfaces, interfaces or in semiconductor quantum wells. The interaction between the spin Pauli matrices vector σ and the momentum k can be expressed by the following Hamiltonian:

where αR is the Rashba coefficient, and  the unit vector perpendicular to the interface (here we focus on interfacial 2DEGs). This interaction leads to dispersion curves and Fermi contours of the type shown in Fig. 1a,b. Such dispersion curves and Fermi contours have been characterized by spectroscopic measurements for many surfaces and interfaces, and large Rashba couplings are generally found with heavy elements of strong SOC such as Bi, Pb, W and so on. The largest Rashba coefficient has been found for an Ag(111) film covered by a
the unit vector perpendicular to the interface (here we focus on interfacial 2DEGs). This interaction leads to dispersion curves and Fermi contours of the type shown in Fig. 1a,b. Such dispersion curves and Fermi contours have been characterized by spectroscopic measurements for many surfaces and interfaces, and large Rashba couplings are generally found with heavy elements of strong SOC such as Bi, Pb, W and so on. The largest Rashba coefficient has been found for an Ag(111) film covered by a  BiAg(111)surface alloy, but very large values have also been found at the interface of Bi with many nonmagnetic materials10,11, not only Ag but also Cu, Si,… (with magnetic materials, however, the competition between exchange interaction and SOC distorts or suppresses the Rashba effect). At the surface or interface of Bi the largest effects are obtained for the (111) orientation in the rhombohedral indexing10,11.
BiAg(111)surface alloy, but very large values have also been found at the interface of Bi with many nonmagnetic materials10,11, not only Ag but also Cu, Si,… (with magnetic materials, however, the competition between exchange interaction and SOC distorts or suppresses the Rashba effect). At the surface or interface of Bi the largest effects are obtained for the (111) orientation in the rhombohedral indexing10,11.
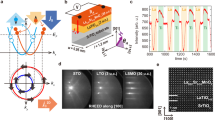
(a) Typical spin-split dispersion curves of a Rashba 2DEG for αR>0 (adapted from Nechaev et al.28) and (b) typical Fermi contours. An electron flow (that is, a shift of the Fermi contours in the direction of the flow) automatically induces a nonzero spin density (REE). Inversely, a nonzero spin density generated by spin injection induces an electron flow (IREE). (c) Scheme of the NiFe/Ag/Bi samples under resonance. The radio frequency (RF) field is along y, and the DC field along x. JS is the vertical DC spin current injected into the Ag/Bi interface states (back flow included), and converted into a horizontal DC charge current IC by the IREE. In an open circuit situation IC is balanced by the current associated to the DC voltage V.
Edelstein12 has been the first to show that a charge current carried by a Rashba 2DEG is automatically associated to a nonzero spin density (spin accumulation). Although additional effects13 are expected in the presence of impurity scattering, our focus here is on this association between charge current and nonzero spin density, what we call the Rashba–Edelstein Effect (REE). At the interface with a magnetic layer, the nonzero spin density can lead to a torque acting on the magnetization of the magnetic layer and, as the SHE, this mechanism has also been proposed to explain experiments of current-induced magnetization switching or domain wall motion14,15.
The objective of our work is to use transport measurements to demonstrate the association between charge current and nonzero spin density in an interfacial Rashba 2DEG. We inject a spin current into a Ag/Bi bilayer by spin pumping from a NiFe layer at its ferromagnetic resonance (FMR)16,17 and we identify the characteristic signature of an Inverse REE (IREE), that is, the generation of a charge current carried by the interfacial states in response to the nonzero spin density induced by the spin injection. This effect for 2D interfacial states is the equivalent of the inverse SHE (ISHE) in bulk materials. Our results represent, at our knowledge, the first observation of the IREE. We present an analysis of our results that introduce an IREE length characterizing the conversion between the injected spin current into a 2D charge current. The efficient conversion from spin-to-charge current found at the Ag/Bi interface shows that the REE could be a major tool for the generation and detection of spin currents or magnetization control.
Results
Experiments
Our spin pumping experiments have been performed on devices of the type represented on Fig. 1b. Four kinds of multilayers have been deposited on Si by evaporation (see § Methods): NiFe, NiFe/Ag, NiFe/Bi and NiFe/Ag/Bi. The texture of the Bi layer is (111) in the rhombohedral notation (see structural characterization in Methods). We did not want to reproduce the complex structure of the  BiAg(111) surface alloy for which the strongest Rashba coupling has been found10 but simply exploit the relatively large Rashba coupling existing at the interface between Bi(111) and many materials (as at the surface of Bi(111))10,11. The thicknesses of the Bi and NiFe layers are 8 and 15 nm, respectively, whereas the thickness of Ag varies from sample to sample (tAg=0, 5, 10 and 20 nm). At the FMR, a vertical direct current (DC) spin current JS (opposite flows of spin up and spin down currents) is injected into the nonmagnetic layers16,17 with the spin polarization axis along x in the situation of Fig. 1c. The IREE of the Ag/Bi interface can then convert this spin current into a DC charge current along y, or, in the situation of an open circuit, give rise to a DC voltage V (Fig. 1c). The charge current IC corresponding to the amplitude V can be written as
BiAg(111) surface alloy for which the strongest Rashba coupling has been found10 but simply exploit the relatively large Rashba coupling existing at the interface between Bi(111) and many materials (as at the surface of Bi(111))10,11. The thicknesses of the Bi and NiFe layers are 8 and 15 nm, respectively, whereas the thickness of Ag varies from sample to sample (tAg=0, 5, 10 and 20 nm). At the FMR, a vertical direct current (DC) spin current JS (opposite flows of spin up and spin down currents) is injected into the nonmagnetic layers16,17 with the spin polarization axis along x in the situation of Fig. 1c. The IREE of the Ag/Bi interface can then convert this spin current into a DC charge current along y, or, in the situation of an open circuit, give rise to a DC voltage V (Fig. 1c). The charge current IC corresponding to the amplitude V can be written as

where a and l are the width and length of the sample, while RS is the sheet resistance of the sample, measured independently using a four probe configuration.
In Fig. 2, we show typical results for (top) the derivative of the ferromagnetic absorption (ferromagnetic spectrum) and (bottom) the corresponding field dependence of IC at the FMR for, respectively, (a) a sample with only an Ag layer below NiFe, (b) a sample with only Bi below NiFe and (c) a sample with a Bi/Ag layer below NiFe. Similar measurements were obtained on four series of samples of different widths and lengths. The variations of RS and IC in our four series of samples are presented in Fig. 3a–c.
FMR spectrum (top) and corresponding field dependence of the current IC derived from the DC voltage V (bottom) for NiFe(15)/Ag(10) (a), NiFe(15)/ Bi(8) (b) and NiFe(15)/Ag(5)/Bi(8) (c) samples. Red lines are Lorentzian fits. The narrow FMR line and negligible DC signal with only Ag in (a) corresponds to negligible spin absorption ( ∼0) and ISHE when the Ag thickness is much smaller than the spin diffusion length (see Supplementary Methods). For the samples in (b,c) the
∼0) and ISHE when the Ag thickness is much smaller than the spin diffusion length (see Supplementary Methods). For the samples in (b,c) the  values derived from FMR and the raw data of DC voltage curves are shown in Methods.
values derived from FMR and the raw data of DC voltage curves are shown in Methods.
(a) Ag thickness dependence of the sheet resistance RS of NiFe/Ag(t)/Bi samples, and a linear fit yielding ρAg=8.3 μΩ cm−1, (b) Ag thickness dependence of the charge current, for one of the NiFe/Ag(t)/Bi sample series (the length l and width a of the samples are, respectively, 2.4 mm and 0.4 mm, the current is normalized for hrf =1 G), (c) as in (b) but for all the series (l=1, 1.5, 2.4 and 3 mm) and (d) for all the series, variation of the ratio λIREE of the horizontal charge current density, jC=IC/a (derived from the DC voltage by Equation 2), to the vertical spin current density jS injected by spin pumping. As jC is in A m−1 and jS in A m−2, λIREE is a length expressed in nm on the figure.
From the results shown in Figs 2 and 3b,c, it first turns out that the largest values of IC are obtained for samples with both Ag and Bi, that is, only when there is an Ag/Bi interface. IC is indeed negligible with only an Ag layer, which means that the contribution from the ISHE in Ag can be neglected, in agreement with the very small SH angle (<0.01, Niimi Y., Otani Y. and Fert A., personal communication) in Ag. Also, in NiFe/Bi samples (samples tAg=0 in Fig. 3b,c), despite injected spin current densities jS similar to those obtained in NiFe/Ag/Bi (see Table 1 and Methods), IC is definitely smaller, which also highlights that having Bi/Ag interfaces is essential to obtain large IC (previous results18 of spin pumping from NiFe directly into Bi layers correspond, after normalization, to IC values similar to ours in samples with only Bi). These observations lead us to the conclusion that the large spin signal that appears in the NiFe/Ag/Bi samples cannot be explained by the ISHE of Ag or Bi, and is due to the IREE introduced by the existence of Ag/Bi interfaces. The definitely smaller value with Bi in direct contact with NiFe probably reflects the smaller Rashba effect due to competition between exchange and SOC at an interface of Bi with a magnetic layer. Note, we can also rule out the signal that could be generated by SHE in a thin layer of AgBi alloy because it has been found that the SHE of AgBi is negative and would give a contribution with the wrong sign (Niimi Y., Otani Y. and Fert A., personal communication).
A second interesting point is that IC in the NiFe/Ag/Bi samples, as well as the vertical spin current density jS (see Methods for the jS evolution), does not decrease for increasing Ag thickness. It shows that the Ag layer acts as a quasi-perfect spin transmitter, which is not surprising since the spin diffusion length in Ag is expected to be much larger (300 nm at room temperature19) than the Ag thicknesses. Also, we can expect a negligible spin absorption in the Bi layer (except in its interfacial states) owing to the conjunction of a large resistivity (≈103 μΩ cm−1) and a relatively long spin diffusion length (50 nm according to Hou18). These negligible absorptions in both Ag and Bi (except in their interfacial states) allow us to work in a simpler picture, in which the spin current jS transmitted from NiFe to the Ag/Bi interfacial states can be expressed by a unique effective spin mixing conductance  (eff to mean that
(eff to mean that  takes into account the back flow and expresses the global spin transmission). We present in Methods the standard calculation of
takes into account the back flow and expresses the global spin transmission). We present in Methods the standard calculation of  from the linewidth change of the FMR spectra for our different samples (including an analysis of the frequency dependence to discriminate between additional damping and additional inhomogeneities). The next step is the calculation of the vertical spin current density jS transferred from the NiFe layer to the Ag/Bi interface. It can be written as20,21:
from the linewidth change of the FMR spectra for our different samples (including an analysis of the frequency dependence to discriminate between additional damping and additional inhomogeneities). The next step is the calculation of the vertical spin current density jS transferred from the NiFe layer to the Ag/Bi interface. It can be written as20,21:

The spin current density at f=9.7 GHz, ω=2πf and hrf=1 G is found to be between 5.5 and 7 MA m−2 for all the NiFe/Ag(t)/Bi samples (see Table 1 and Methods). This vertical 3D spin current is converted by the IREE into the interface current IC (cf. Fig. 1) corresponding to a 2D current density (in A m−1), jC=IC/a. The ratio jC/jS is the length λIREE shown in Fig. 3d and characterizing the conversion between the injected 3D spin current into a 2D charge current at the Ag/Bi interface.
Analysis of the IREE
The conversion by IREE between the spin density injected into interface states and the resulting lateral charge current density can be related to the Rashba coupling (cf. Equation 1) in a simple model based on the standard picture of the REEs. For the two Fermi contours of Rashba 2D electrons, the relation between the 2D spin densities δs± along the x axis and the 2D charge current densities along y can be written as22:

where + and − refer to the two Fermi contours, while kF+ and kF− are their two Fermi radii (supposing free-electron-like circular contours). Introducing the splitting between the two radii induced by the Rashba interaction,

gives the 2D charge current density associated with the total 2D spin density ‹δs›=δs++δs−

In our experiments, the out-of-equilibrium spin density ‹δs› in the interface states is the result of the injection of a vertical spin current density jS. At this point, we suppose that the spin current transmission from NiFe through Ag into these interface states is independent of the electron momentum and can be described by the unique effective spin mixing conductance  that we have derived from the variation of the damping in NiFe. The assumption of a momentum-independent spin mixing conductance implies a diffuse transmission into the states of a rough enough interface (no momentum-selecting specular transmission/reflection, introducing momentum selection would introduce some changes in the numerical factors). In these conditions, there is a simple linear relation between the 2D spin density ‹δs› of Equation 6 and the 3D vertical spin current jS given by Equation 3:
that we have derived from the variation of the damping in NiFe. The assumption of a momentum-independent spin mixing conductance implies a diffuse transmission into the states of a rough enough interface (no momentum-selecting specular transmission/reflection, introducing momentum selection would introduce some changes in the numerical factors). In these conditions, there is a simple linear relation between the 2D spin density ‹δs› of Equation 6 and the 3D vertical spin current jS given by Equation 3:

where τS is an effective relaxation time expressing the balance between spin injection and spin density in relation with the coupled spin-momentum scattering. From Equations 6 and 7 we find:

with

where jC is in A m−1, jS is in A m−2 and λIREE has the dimension of a length. Our experimental results, with jC derived from the DC signal and jS derived, respectively, from Equation 3, correspond to values of λIREE shown in Fig. 3c and ranging from 0.2 to 0.33 nm in our four series of samples.
Equation 9 can be compared with the corresponding equation for the current density induced by ISHE (2D current density after integration on the layer thickness of the ISHE layer).

where  , λsf and t are the spin Hall angle, the spin diffusion length and the thickness of the nonmagnetic layer. In the limit t<<λsf, Equation (10) can also be written
, λsf and t are the spin Hall angle, the spin diffusion length and the thickness of the nonmagnetic layer. In the limit t<<λsf, Equation (10) can also be written

Although it is unphysical to ascribe a ‘thickness’ to 2D interfacial states, we can try to see what would give an interpretation of our result by the ISHE in an ‘interface layer’ of typical thickness t=0.4 nm (implicitly <<λsf). For example, our experimental result giving λIREE=0.3 nm would be accounted for by an ISHE with  t=0.3 nm, what gives an unphysical SHE angle of 1.5. It rules out an identification of the IREE to some type of ISHE type in a layer of interface states. The comparison with ISHE simply shows the importance of the spin-orbit effects (IREE) induced by the Ag/Bi interface. More generally, if bulk effects (SHE and ISHE) in a layer of thickness t and interfacial effects (REE and IREE) coexist, it is straightforward to see that the interfacial effects will appear as a contribution to the SH angle inversely proportional to t in an interpretation by only SHE or ISHE.
t=0.3 nm, what gives an unphysical SHE angle of 1.5. It rules out an identification of the IREE to some type of ISHE type in a layer of interface states. The comparison with ISHE simply shows the importance of the spin-orbit effects (IREE) induced by the Ag/Bi interface. More generally, if bulk effects (SHE and ISHE) in a layer of thickness t and interfacial effects (REE and IREE) coexist, it is straightforward to see that the interfacial effects will appear as a contribution to the SH angle inversely proportional to t in an interpretation by only SHE or ISHE.
The meaning of the time τS expressing the relaxation of the spin/momentum polarization of the Rashba Fermi discs is not clear at this stage of interpretation. With a mean value of λIREE equal to 0.3 nm and the value αR=0.56 × 10−10 eVm given by Ast et al.10 for the Rashba coefficient at the surface of Bi(111), Equation 9 leads to τS=0.5 × 10−14 s, which is not unreasonable for coupled spin-momentum scattering of interfacial states at a rough interface. In terms of level broadening, one obtains ħ/τS=0.18 eV, which is several times smaller than the Rashba spin splitting at EF found by spectroscopic measurements at the Bi(111) surface, about 0.8 eV in Koroteev11 and 0.5 eV in Ohtsubo23. This justifies our approach in a Rashba splitting picture of the interface states, at least in first approximation. It would be interesting to check whether more perfect interfaces24 with more precisely defined Rashba levels can enhance the effects we observe. Actually our results should motivate similar experiments on different type of Bi interfaces as well as on interfaces of other materials with strong SO coupling (Pb, W and so on). On the side of the theoretical picture, the assumption of the isotropic Rashba coupling of Equation 1 appear today to be an approximation and recent spectroscopic studies23 have shown that the real Fermi contours are far from the circles of Fig. 1b. Ab-initio calculations are certainly needed for a better description of the interface states. Also, for a more quantitative interpretation, one should go beyond the simple assumption of a momentum-independent transmission to the interface states of our article.
Discussion
The conversion between spin and charge current using the Rashba coupling of interface states opens a promising way for the generation and the detection of spin currents in spintronic devices. In complement to SHE, it sets the basis of a spintronics without ferromagnets. In view of its efficiency, the REEs could in several cases complement or replace the SHE in order to generate, amplify or detect spin excitations, or to induce magnetic precessions or magnetization switching. An example of application could be the conversion of heat into electrical power by conversion first from heat flow into spin current using spin Seebeck effect and then into charge current by ISHE or IREE25. With IREE at the interface between insulating materials an important advantage for this device would be the larger resistance of a 2DEG and the resulting larger RI2 power. This should incite research efforts on the other types of interfaces with large Rashba coupling revealed by spectroscopic measurements during the recent years.
Note added on proof: after submission of our article we received a preprint of a theoretical treatment of the IREE, see Shen et al., Inverse Edelstein Effect, arXiv: 1311.6516v1. The final result of this model is similar to Equations (8) and (9) in our paper. However, in the weak spin-orbit limit of Shen's model (‘diffusive regime’), the relaxation time τ turning out in the final expression is the momentum relaxation time, whereas, in our strong spin-orbit picture, there is a single relaxation time for momentum and spin that we have called τs.
Methods
Sample structure and structural characterizations
The samples were fabricated by successive evaporation in ultra-high vacuum of Bi, Ag and NiFe using a Si wafer substrate covered by 500 nm of a thermally oxidized SiO2 (ref. 26). All samples were prepared using the same deposition conditions.
X-ray reflectivity and X-ray diffraction measurements were performed with a Co Kα radiation on Ag/Bi//SiO2 samples (See Fig. 4a). At low angle the X-ray reflectivity scan could be nicely fitted, the results showing that the thicknesses of the layers are similar to the nominal ones (taken from the quartz balance in the evaporation chamber). However, the roughness is relatively large: around 1.5 nm at the Bi/Ag interface, and around 3.5 nm at the Ag surface. Similarly, in the sample without Ag, the roughness of the Bi surface is around 3.5 nm. In Fig. 4b the X-ray diffraction scans performed on Ag(20)/Bi(8)//SiO2 sample are displayed. As shown in previous works by some of the authors26,27, one can notice that the Bi layer is textured in the (001) direction following the usual description of a rhombohedral crystallography phase with a hexagonal setting, that is, the growth direction is along the c axes of such hexagonal cell. Note that the (001) direction of the hexagonal setting corresponds to the (111) direction of the rhombohedral primitive cell. For Ag, the cubic phase is observed with mainly (220) texture.
(a) XRR scans of the Ag(t)/Bi (8)//SiO2 samples (thicknesses in nm). Red lines are theoretical fits. The thicknesses are close to the nominal ones, but the roughness at the interfaces is between 1.5 and 3.5 nm. (b) XRD scans of the Ag(20)/Bi(8)//SiO2 sample. The top curve is the standard θ–2θ curve and the bottom curve is the acquisition with an off axis of 1 degree to reduce the intensity of the Si substrate. A strong growth texture of rhombohedral Bi along the (001) direction is found (corresponding to (111) in the primitive rhombohedral cell). The silver layer grows in the cubic crystallography phase with a texture in the (220) direction and a much smaller contribution of the (200) texture.
High-angle annular dark field (HAADF) Scanning Transmission Electron Microscopy combined with energy dispersive X-ray spectroscopy (EDX) has been performed in an FEI Titan microscope operated at 300 kV and equipped with a probe aberration corrector, a high-brightness field emission gun (X-FEG) and an EDAX X-ray spectrometer. In the Scanning Transmission Electron Microscopy-EDX experiment, the electron probe, of an approximate size of 1 Å, is scanned through the sample. While the position of the beam is monitored by collecting the transmitted signal scattered at high angles with an annular dark-field detector (HAADF imaging), the X-rays emitted by the specimen at each position are detected simultaneously. The lamella for the cross-sectional TEM study has been fabricated in an FEI Helios 600 Nanolab with the ion column operated at 5 kV during final thinning to avoid sample amorphization. Figure 5a shows the HAADF image of the cross-sectional view of one of the films grown, with nominal thicknesses (in nm) Bi(8)/Ag(20)/NiFe(15). The image indicates that the Bi, Ag and FeNi layers are continuous with a roughness in agreement with X-Rays data. The sample composition has been analysed by EDX measurements in line scans along the layers stack. The typical obtained result is shown in Fig. 5b. As expected, the order of the observed signals is Si-Bi-Ag-Ni, corresponding, respectively, to the substrate and the Bi, Ag and NiFe layers. The signals correspond, respectively, to the Si-K, Bi-L, Ag-L and Ni-K emission lines. The intensity for each element is broadened due to the interaction volume of the electron beam in the lamella and delocalization effects of the electron beam. The layers thicknesses can be estimated from the full-width half maximum intensity values. The following values are obtained: Bi (6), Ag (22) and Ni (16), which is in good correspondence with the nominal values.
FMR and voltage measurements
Simultaneous measurements of the FMR and DC transversal voltage have been carried out on the different deposits (NiFe, NiFe/Ag, NiFe/Bi and NiFe/Ag/Bi). The Ferromagnetic dependence of resonance field and peak-to-peak linewidth are presented in Fig. 6. For each deposit, three different preparation methods have been used, leading to different sample lengths and shapes.
Results on NiFe(15)/Ag(t)/Bi(8)). (a) In-plane dispersion relationship of resonance conditions, fitted according to Supplementary Equation S1. (b) Frequency dependence of the peak-to-peak linewidth. The lines correspond to the linear fit of Supplementary Equation S2.
One and 1.5 mm long samples were prepared using mechanical mask and two steps of ion Ar+ plasma etching, controlled in-situ by secondary ion mass spectrometry analysis. The first step defines the length l of the ferromagnet, the etching being stopped after the removal of the NiFe layer. The other step defines the width a of the sample, the etching process being stopped at the surface of the substrate (Fig. 7a shows the scheme of the electrical connections in this geometry).
Three millimetres long samples have been prepared using a single ion milling step. The active part is protected using a mechanical mask, and the full stack is etched so that a rectangular bar remains.
Finally, 2.4 mm long samples were made by cutting small rectangular pieces of 0.4 mm width, without etching (Fig. 7b shows the scheme of the electrical connections in this geometry). Note that, whatever the preparation method, all samples corresponding to a given stack (for example, NiFe/Bi) come from the same deposit.
The increase of the damping constant induced by spin pumping has been derived from measurements of the FMR peak-to-peak linewidth. The frequency dependence of the linewidth has been used in order to discriminate the contribution from spin pumping and frequency independent contribution due to inhomogeneities. The difference between the damping in the studied sample, αeff, and the damping in a single NiFe(15) reference layer,α0, gives the effective spin mixing conductivity22:

where Meff, tF, g and μB are the effective saturation magnetization, the thickness of the ferromagnetic layer, the Landé factor and the Bohr magnetization, respectively.
The results of the frequency dependence of both the resonance field and the peak-to-peak linewidth are shown in Fig. 6a,b, together with the previous results on the single NiFe(15) film layer. We can clearly observe an enhancement of the damping constant (slope in Fig. 6b). Additionally the FMR measurements, where the DC magnetic field is applied parallel and perpendicular to the film plane, allow us to calculate the g-Landé factor, which is found to be around 2.11 (as in the reference sample). The effective magnetic saturation of the four samples lies between 650 and 670 emu cm−3 (lower than in the reference sample, 715 emu cm−3) and the ΔH0 contribution to the linewidth was between 15 and 25 G (higher than in the reference sample, 0.6 G). The last results could be due to the interface roughness mentioned previously.
Table 1 summarizes the results of the damping constant measurements made in the NiFe/Ag/Bi series, of the effective spin mixing conductivity  measurements (cf. Equation 12), and of the injected spin current density calculations at the interface (cf., Equation 3). The jS value practically does not change with small shifts of the frequency, but changes strongly with the hrf values. The jS values in Table 1 were calculated for hrf=1 G and f=9.7 GHz. At 9.6 GHz, for series with l=3 mm, and 9.75 Ghz for series with l=2.4 mm, jS slightly changes, but it is taken into account. Note that the experimental hrf values in all the measurements were already taken into account in the average voltage.
measurements (cf. Equation 12), and of the injected spin current density calculations at the interface (cf., Equation 3). The jS value practically does not change with small shifts of the frequency, but changes strongly with the hrf values. The jS values in Table 1 were calculated for hrf=1 G and f=9.7 GHz. At 9.6 GHz, for series with l=3 mm, and 9.75 Ghz for series with l=2.4 mm, jS slightly changes, but it is taken into account. Note that the experimental hrf values in all the measurements were already taken into account in the average voltage.
The schematic geometries and electrical contacts for the different series are shown in Fig. 7. Samples with the same length and the two geometries (t=10 nm of Ag) have been made to check that both geometries yields the same voltage amplitude.
Electrical connections are realized using wire bonding, and a sample holder made of a printed circuit board circuit, on which the samples are glued. To perform the measurements, the sample is placed in the center of a cylindrical X-band resonator cavity (f∼9.5 GHz, TE011 mode). The linear dependence of the DC voltage amplitude with the microwave applied power has been verified. The applied power of the microwave excitation showed in Fig. 2 was 200 mW.
To ensure that the symmetrical DC signal of the spin pumping experiment has no contribution from the planar Hall effect in the NiFe layer, the same measurement has been performed with only a NiFe(15 nm) layer. This reference sample exhibits a transverse voltage with a mostly asymmetrical Lorentzian shape, that can be ascribed to the planar Hall effect (see Supplementary Methods and Supplementary Fig. S1). The absence of a significant symmetrical peak for this reference sample, as it is expected in resonator cavities with the TE011 mode, implies that the symmetrical voltage observed in all the other samples indeed comes from spin effects.
The bandwidth Δf and the quality factor Q of the cavity were measured to calculate the microwave magnetic field strength. Knowing the radio frequency field hrf and the effective damping constant, the spin current density due to spin pumping can then be estimated for all FM/NM layers using Equation (3). To check the good placement of the samples in the electrical field node of the cavity, we checked the reproducibility of the measurement by turning the sample in the sample plane by 180° with respect to the DC magnetic field. As  was found to be slightly different in the parallel (H applied as shown in Fig. 1) and antiparallel cases, it has been averaged to calculate λIREE (ref. 20). The corresponding raw data for the sample with l=1 mm are shown in Fig. 8, whereas the three other series are presented in the Supplementary Information S3–S5. The resulting currents produced by spin pumping and IREE are summarized in Fig. 3c. Results of the NiFe/Ag sample are presented in Supplementary Methods and Supplementary Fig. S2.
was found to be slightly different in the parallel (H applied as shown in Fig. 1) and antiparallel cases, it has been averaged to calculate λIREE (ref. 20). The corresponding raw data for the sample with l=1 mm are shown in Fig. 8, whereas the three other series are presented in the Supplementary Information S3–S5. The resulting currents produced by spin pumping and IREE are summarized in Fig. 3c. Results of the NiFe/Ag sample are presented in Supplementary Methods and Supplementary Fig. S2.
Raw data of FMR-V curves on NiFe(15)/Ag(t)/Bi(8), in the series with length of 1.0 mm. (a) 0 nm of Ag. (b) 5 nm of Ag. (c) 10 nm of Ag. (d) 20 nm of Ag. The two voltage curves correspond to the parallel and antiparallel cases. Black and blue experimental data stand for θH equal +90° and −90°, respectively. The red lines are lorentzian fits. The hrf fields are around 1 G. The results for the three others series are presented in Supplementary Figs S3–S5.
Additional information
How to cite this article: Rojas Sánchez, J. C. et al. Spin-to-charge conversion using Rashba coupling at the interface between non-magnetic materials. Nat. Commun. 4:2944 doi: 10.1038/ncomms3944 (2013).
References
Maekawa S. (ed.)Concepts in Spin Electronics Oxford University Press (2006).
Maekawa S., Valenzuela S. O., Saitoh E., Kimura T. (eds)Spin Currents Oxford University Press (2012).
Dyakonov, M. I. & Perel, V. I. Current-induced spin orientation of electrons in semiconductors. Phys. Lett. A 35, 459 (1971).
Kato, Y. K., Myers, R. S., Gossard, A. C. & Awschalom, D. D. Observation of the Spin Hall Effect in Semiconductors. Science 306, 1910–1913 (2004).
Valenzuela, S. O. & Tinkham, M. Direct electronic measurements of the spin Hall effect. Nature 442, 176–179 (2006).
Manchon, A. & Zhang, S. Theory of nonequilibrium intrinsic spin torque in a single nanomagnet. Phys. Rev. B 78, 212405 (2008).
Liu, L. et al. Spin-torque switching with the giant spin hall effect of tantalum. Science 336, 555–558 (2012).
Khvalkovskiy, A. V. et al. Matching domain-wall configuration and spin-orbit torques for efficient domain-wall motion. Phys. Rev. B 87, 020402 (R) (2013).
Bychkov, Y. A. & Rashba, E. I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 39, 78–81 (1984).
Ast, C. R. et al. Giant spin splitting through surface alloying. Phys. Rev. Lett. 98, 186807 (2007).
Koroteev, Y. M. et al. Strong Spin-Orbit splitting on Bi surfaces. Phys. Rev. Lett. 93, 046403 (2004).
Edelstein, V. M. Spin polarization of conduction electrons induced by electric current in two-dimensionalasymmetric electron systems. Solid State Commun. 73, 233–235 (1990).
Raimondi, R., Schwab, P., Gorini, C. & Vignale, G. Spin-orbit interaction in a 2DEG: a SU(2) formulation. Ann. Phys. (Berlin) 524, 153 (2012).
Miron, I. M. et al. Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nature Mater. 9, 230–233 (2010).
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Tserkovnyak, Y., Brataas, A. & Bauer, G. E. W. Enhanced Gilbert Damping in Thin Ferromagnetic Films. Phys. Rev. Lett. 88, 117601 (2002).
Saitoh, E., Ueda, M., Miyajima, H. & Tatara, G. Conversion of spin current into charge current at room temperature: Inverse spin-Hall effect. Appl. Phys. Lett. 88, 182509 (2006).
Hou, et al. Interface induced inverse spin Hall effect in bismuth/permalloy bilayer. Appl. Phys. Lett. 101, 042403 (2012).
Fukuma, Y. & Wang, L. et al. Giant enhancement of spin accumulation and long-distance spin precession in metallic lateral spin valves. Nature Mater. 10, 527–531 (2011).
Ando, K. et al. Inverse spin-Hall effect induced by spin pumping in metallic system. J. Appl. Phys. 109, 103913 (2011).
Mosendz, O. et al. Detection and quantification of inverse spin Hall effect from spin pumping in permalloy/normal metal bilayers. Phys. Rev. B 82, 214403 (2010).
Gambardella, P. & Miron, I. M. Current-induced spin-orbit torques. Philos. Trans. A Math. Phys. Eng. Sci. 369, 3175–3197 (2011).
Ohtsubo, Y. et al. Giant anisotropy of spin-orbit splitting at the bismuth surface. Phys. Rev. Lett. 109, 226404 (2012).
Xiao, S., Wei, D. & Jin, X. Bi(III) thin film with insulating interior but metallic surfaces. Phys. Rev. Lett. 109, 166805 (2012).
Bauer, G. E. W., Saitoh, E. & van Wees, B. J. Spin caloritronics. Nat. Mat. 11, 391–399 (2012).
Marcano, N. et al. Structural and magnetotransport properties of Bi thin films grown by thermal evaporation. J. Magn. Magn. Mater. 322, 1460–1463 (2010).
Marcano, N. et al. Role of the surface states in the magnetotransport properties of ultrathin bismuth films. Phys. Rev. B 82, 125326 (2010).
Nechaev, I. A. et al. Hole dynamics in a two-dimensional spin-orbit coupled electron system: Theoretical and experimental study of the Au(111) surface state. Phys. Rev. B 80, 113402 (2009).
Acknowledgements
We thank S. Blugel, F. Freimuth, Xiafeng Jin, R. Raimondi, M. Miron, G. Gaudin, A. Marty and A. Manchon for fruitful discussions. Assistance of I. Rivas, R. Valero, G. Simón, L. Casado and R. Córdoba (LMA laboratory, Zaragoza) during sample and lamellae preparation is acknowledged. Strip line experiments were performed with the help of A. Gosh, W.E. Bailey and U. Ebels. Previous discussions on the properties of bismuth with S. Sangiao, L. Morellón, N. Marcano, M.C. Martínez-Velarte and M.R. Ibarra are acknowledged. Financial support from the MAT2011-27553-C02 project, funded by the Spanish Ministry of Economy (including FEDER funding) and from the French Agence National de la Recherche ANR-10-BLANC-SPINHALL are acknowledged. J.C.R.S. acknowledges the CEA-Eurotalents program for its initial support.
Author information
Authors and Affiliations
Contributions
A.F. proposed the experiment. A.F., L.V., J.C.R.S. and J.M.D.T. managed the project. J.C.R.S., C.M., S.G. and G.D. performed the experiments. J.C.R.S., J.P.A., L.V., J.M.D.T. and A.F. took care of the data analysis and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S5, Supplementary Methods and Supplementary References (PDF 785 kb)
Rights and permissions
About this article
Cite this article
Sánchez, J., Vila, L., Desfonds, G. et al. Spin-to-charge conversion using Rashba coupling at the interface between non-magnetic materials. Nat Commun 4, 2944 (2013). https://doi.org/10.1038/ncomms3944
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms3944
This article is cited by
-
The central role of tilted anisotropy for field-free spin–orbit torque switching of perpendicular magnetization
NPG Asia Materials (2024)
-
Local symmetry breaking drives picosecond spin domain formation in polycrystalline halide perovskite films
Nature Materials (2023)
-
Observation of the orbital inverse Rashba–Edelstein effect
Nature Physics (2023)
-
Phase biasing of a Josephson junction using Rashba–Edelstein effect
Nature Communications (2023)
-
Unraveling the spin current hermiticity
Journal of Materials Science (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.