Abstract
Percolation theory concerns the emergence of connected clusters that percolate through a networked system. Previous studies ignored the effect that a node outside the percolating cluster may actively induce its inside neighbours to exit the percolating cluster. Here we study this inducing effect on the classical site percolation and K-core percolation, showing that the inducing effect always causes a discontinuous percolation transition. We precisely predict the percolation threshold and core size for uncorrelated random networks with arbitrary degree distributions. For low-dimensional lattices the percolation threshold fluctuates considerably over realizations, yet we can still predict the core size once the percolation occurs. The core sizes of real-world networks can also be well predicted using degree distribution as the only input. Our work therefore provides a theoretical framework for quantitatively understanding discontinuous breakdown phenomena in various complex systems.
Similar content being viewed by others
Introduction
Percolation transition on complex networks occurs in a wide range of natural, technological and socioeconomic systems1,2,3. The emergence of macroscopic network connectedness, due to either gradual addition or recursive removal of nodes or links, can be related to many fundamental network properties, for example, robustness and resilience4,5, cascading failure3,6,7, epidemic or information spreading8,9 and structural controllability11,12. Particularly interesting are the emergence of a giant connected component13,14,15,16,17,18,19,20,21, the K-core (obtained by recursively removing nodes with degree less than K)22,23,24,25, and the core (obtained by recursively removing nodes of degree one and their neighbours)12,26,27.
These classical percolation processes are passive in the sense that whether or not a node belongs to the percolating cluster depends only on its number of links to the percolating cluster. However, in many physical or information systems, each node has an intrinsic state and after a node updates its state, it can actively induce its neighbours to update their states too. One example is the frozen-core formation in Boolean satisfiability problems28, where non-frozen nodes can induce its frozen neighbours into the non-frozen state (the so-called whitening process29,30,31). In the glassy dynamics of kinetically constrained models, a spin in a certain state facilitates the flipping of its neighbouring spins32. In inter-dependent networks, a collapsed node of one network causes the failure of the connected dependent node in the other network3,33, resulting in a damage cascading process. The inducing effect can also be related to information or opinion spreading, for example, an early adopter of a new product or innovation might persuade his or her friends to adopt either.
Despite its implications on a wide range of important problems, the inducing effect on percolation transitions has not been fully understood. In this work, we study the inducing effect on the classical site percolation and K-core percolation in complex networks. We analytically show that the inducing effect always causes a discontinuous percolation transition, therefore providing a new perspective on abrupt breakdown phenomena in complex networked systems. Our analytical calculations are confirmed by extensive numerical simulations.
Results
Description of the model
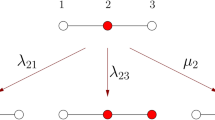
We assume each node of the network has a binary internal state: protected or unprotected. We allow an initial p fraction of nodes randomly chosen from the network to be protected. If p=1, all the nodes are initially protected. As time evolves, a protected node spontaneously becomes unprotected if it has less than K protected neighbours. (In case of K=0, a protected node will never spontaneously become unprotected.) A protected node with K or more protected neighbours will be induced to the unprotected state if at least one of its unprotected neighbours has less than K′ protected neighbours. (In case of K′=0 or 1, the inducing effect is absent and our model reduces to the classical site percolation or K-core percolation.) Note that once a node becomes unprotected it will remain unprotected.
We refer to the above-mentioned evolution process as the (K, K′)-protected core percolation. The (K, K′)-protected core, or simply, the protected core is the subnetwork formed by all the surviving protected nodes and the links among them (see Fig. 1 for an example). We denote the total number of nodes in the protected core as Np-core. We can prove that the protected core is independent of the particular state evolution trajectory of the nodes and hence is well defined (see Supplementary Note 1).
In the context of opinion spreading or viral marketing, the (K, K′)-protected core percolation can be described as follows: consider a population of users to adopt a new product (or idea, opinion, innovation and so on). Initially there is a p fraction of users in the ‘protected’ (or conservative) state and refuse to adopt the new product. The other (1–p) fraction of users are in the ‘unprotected’ state, that is, they are early adopters. A conservative user will automatically adopt the new product if he/she has less than K conservative friends. An adopted user with less than K′ conservative friends will persuade all his or her conservative friends to adopt the new product. Then the protected core, if exists, can be viewed as the subnetwork of the most conservative individuals, who will never adopt the new product.
Analytical approach
Consider a large uncorrelated random network containing N nodes, with arbitrary degree distribution P(k) and mean degree  34,35. We assume that if any node i is still in the protected state, its neighbours do not mutually influence each other and therefore their states are independently distributed. This is a slight extension of the Bethe–Peierls approximation widely used in spin-glass theory and statistical inference36. Note that a closely related approximation in network science is the tree approximation5,14,34, which assumes the neighbours of node i become disconnected if i is removed from the network. Under our assumption of state independence, we can calculate the normalized size np-core (≡Np-core/N) of the protected core as
34,35. We assume that if any node i is still in the protected state, its neighbours do not mutually influence each other and therefore their states are independently distributed. This is a slight extension of the Bethe–Peierls approximation widely used in spin-glass theory and statistical inference36. Note that a closely related approximation in network science is the tree approximation5,14,34, which assumes the neighbours of node i become disconnected if i is removed from the network. Under our assumption of state independence, we can calculate the normalized size np-core (≡Np-core/N) of the protected core as

with  being the binomial coefficient (see Supplementary Note 2). The parameter α denotes the probability that, starting from a node i that is still in the protected state, a node j reached by following a randomly chosen link (i, j) is in the unprotected state and having at most K′–1 protected neighbours (including i). The parameter β is the probability that such a node j is in the unprotected state but having at least K′ protected neighbours. We further define γ as the probability that such a node j is in the protected state and having exactly K protected neighbours. Note that if initially we randomly choose a finite p fraction of nodes to be protected, then (1–p) fraction of the nodes will be and remain unprotected. Let us define η as the probability that, starting from such an initially unprotected node m, a node n reached by following a randomly chosen link (m, n) will eventually be in the unprotected state even if the inducing effect of node m is not considered.
being the binomial coefficient (see Supplementary Note 2). The parameter α denotes the probability that, starting from a node i that is still in the protected state, a node j reached by following a randomly chosen link (i, j) is in the unprotected state and having at most K′–1 protected neighbours (including i). The parameter β is the probability that such a node j is in the unprotected state but having at least K′ protected neighbours. We further define γ as the probability that such a node j is in the protected state and having exactly K protected neighbours. Note that if initially we randomly choose a finite p fraction of nodes to be protected, then (1–p) fraction of the nodes will be and remain unprotected. Let us define η as the probability that, starting from such an initially unprotected node m, a node n reached by following a randomly chosen link (m, n) will eventually be in the unprotected state even if the inducing effect of node m is not considered.
Because of the inducing effect, each node j mediates strong correlations among the states of its neighbouring nodes if it is in the unprotected state. After a careful analysis of all the possible microscopic inducing patterns following the theoretical method of Zhou37,38, we obtain a set of self-consistent equations for the probabilities α, β, γ and η:




where Q(k) ≡ kP(k)/c is the degree distribution for the node at an end of a randomly chosen link. These equations can be understood as follows. The first term on the right hand side of Equation (2) is the probability that a node j reached by following a link (i, j) is initially unprotected and having at most K′–2 protected neighbours (excluding node i) without considering its inducing effect. The other two terms in the right hand side of Equation (2) yield the probability that an initially protected node j at the end of a link (i, j) will either spontaneously transit to or be induced to the unprotected state and, when it is still in the protected state, at most K′–2 of its protected neighbours (excluding node i) have more than K protected neighbours themselves. The terms in Equations (3)–(5), can be understood similarly (see Supplementary Note 2 for more explanations).
The above self-consistent equations can be solved using a simple iterative scheme (see Supplementary Note 3). When K, K′≥2, these equations always have a trivial solution (α,β,γ,η)=(1,0,0,1), yielding no protected core (np-core=0). This solution is always locally stable, and it is the only solution if the mean degree c of the network is small or the initial fraction p of protected nodes is small (see Supplementary Note 4). As c (or p) increases, another stable solution of Equations (2)–(5) appears at the critical mean degree c=c* (or the critical fraction p=p*), corresponding to the percolation transition. In the limiting cases of Kε{0,1}, Equations (2)–(5), also change from having only one stable solution to having two distinctive stable solutions at certain critical value c=c* or p=p* (see Supplementary Note 4).
The minimal inducing effect
The minimal inducing effect on percolation transitions can be demonstrated by comparing (0,1)- and (1,1)-protected core percolation transitions with (0,2)- and (1,2)-protected core percolation transitions as we tune the initial fraction of protected node p. Note that the (K,1)-protected core percolation with Kε{0,1} is essentially the classical site percolation1,5,14, because a protected node will remain protected if it has at least one protected neighbour and there is no inducing effect at all. In this case, a giant connected component of protected nodes gradually emerges in the network as p exceeds  (see Fig. 2). The minimal inducing effect is naturally present in the (0,2)- and (1,2)-protected core percolation problems, namely if an unprotected node has only one protected neighbour, this neighbour will be induced to the unprotected state. In this case our analytical calculation shows that both the normalized size of the protected core and that of its giant connected component will jump from zero to a finite positive value at certain critical value p* (see Supplementary Notes 4 and 5). For Erdös–Rényi (ER) random networks39,40 with mean degree c=10, this threshold fraction is p*≈0.44 (for K=1) and p*≈0.42 (for K=0), which are much larger than the threshold value p*=0.1 of the classical continuous site percolation transition (see Fig. 2). Note that in case K=0, a protected node will never spontaneously become unprotected, hence the discontinuous (0,2)-protected core percolation transition is solely due to the inducing effect.
(see Fig. 2). The minimal inducing effect is naturally present in the (0,2)- and (1,2)-protected core percolation problems, namely if an unprotected node has only one protected neighbour, this neighbour will be induced to the unprotected state. In this case our analytical calculation shows that both the normalized size of the protected core and that of its giant connected component will jump from zero to a finite positive value at certain critical value p* (see Supplementary Notes 4 and 5). For Erdös–Rényi (ER) random networks39,40 with mean degree c=10, this threshold fraction is p*≈0.44 (for K=1) and p*≈0.42 (for K=0), which are much larger than the threshold value p*=0.1 of the classical continuous site percolation transition (see Fig. 2). Note that in case K=0, a protected node will never spontaneously become unprotected, hence the discontinuous (0,2)-protected core percolation transition is solely due to the inducing effect.
Symbols are simulation results on a single ER random network of N=106 nodes and mean degree c=10, whereas the lines are theoretical predictions at N=∞. The giant connected component of protected nodes continuously emerges in the (0,1)- and (1,1)-protected core percolation problems (without inducing effect), but it emerges discontinuously in the (0,2)- and (1,2)-protected core percolation problems (with minimal inducing effect).
Inducing effect on K-core percolation
The inducing effect can also be demonstrated by comparing the K-core percolation and the (K, K′)-protected core percolation as we tune the mean degree c. In the following discussions, we set p=1 and focus on the representative case of K′=K (the results for p<1 and 2≤K′≠K are qualitatively the same). And we refer to (K, K)-protected core simply as K-protected core.
We find that for any K≥2, as c reaches the critical value c*, np-core jumps from zero to a finite value  (see Supplementary Note 4), indicating a discontinuous percolation transition. We also find that for any K≥2 and independent of network types,
(see Supplementary Note 4), indicating a discontinuous percolation transition. We also find that for any K≥2 and independent of network types,  in the supercritical regime where c–c*→0+ (see Supplementary Note 6). Such a hybrid phase transition and the associated critical exponent 1/2 were also observed in K-core percolation and core percolation12,22,23,24.
in the supercritical regime where c–c*→0+ (see Supplementary Note 6). Such a hybrid phase transition and the associated critical exponent 1/2 were also observed in K-core percolation and core percolation12,22,23,24.
In the following, we study the discontinuous 2-protected core percolation in a series of random networks with specific degree distributions. We first consider the ER random network with Poisson degree distribution P(k)=e−cck/k!. We find that the discontinuous 2-protected core percolation transition occurs at c=c*≈3.92, with a jump of np-core from zero to  (see Fig. 3). Note that for ER random networks the classical 2-core and core percolation transitions occur at c*=1 and c*=e≈2.72, respectively, and they are both continuous12,24. Hence, allowing unprotected nodes to induce other nodes not only delays the occurrence of the percolation transition to a larger value of c but also makes it discontinuous (see Fig. 4).
(see Fig. 3). Note that for ER random networks the classical 2-core and core percolation transitions occur at c*=1 and c*=e≈2.72, respectively, and they are both continuous12,24. Hence, allowing unprotected nodes to induce other nodes not only delays the occurrence of the percolation transition to a larger value of c but also makes it discontinuous (see Fig. 4).
The degree exponents of the SF networks are λ=3.5,3.0,2.75,2.5 (from left to right). Lines are analytic predictions for infinite system (N=∞), circles and diamonds are exact results obtained through the state evolution process; star and cross symbols are the analytic results using the exact degree sequences of the constructed networks. Each simulation point is obtained by averaging over 80 independent network instances. Note that for λ<3, especially when λ→2, significant finite-size effect is observed. This is rooted in the intrinsic degree correlations in the static model when λ<341,42,43.
Scale-free (SF) networks characterized by a power-law degree distribution  with degree exponent λ are ubiquitous in real-world complex systems39. Interestingly, we find that for purely scale-free networks with P(k)=k−λ/ζ(λ) and ζ(λ) the Riemann ζ function, the K-protected core does not exist for any λ>2 (see Supplementary Note 7). If the smallest degree kmin≥K and a fraction ρ of the links are randomly removed from the purely SF network, then a discontinuous K-protected core percolation transition will occur (see Supplementary Note 7). For asymptotically SF networks generated by the static model with
with degree exponent λ are ubiquitous in real-world complex systems39. Interestingly, we find that for purely scale-free networks with P(k)=k−λ/ζ(λ) and ζ(λ) the Riemann ζ function, the K-protected core does not exist for any λ>2 (see Supplementary Note 7). If the smallest degree kmin≥K and a fraction ρ of the links are randomly removed from the purely SF network, then a discontinuous K-protected core percolation transition will occur (see Supplementary Note 7). For asymptotically SF networks generated by the static model with  for large k only41,42,43, the K-protected core develops when the mean degree c exceeds a threshold value c*. For this type of random networks with different values of c and λ, we compare the theoretical and simulation results and find that they agree well with each other (see Fig. 3).
for large k only41,42,43, the K-protected core develops when the mean degree c exceeds a threshold value c*. For this type of random networks with different values of c and λ, we compare the theoretical and simulation results and find that they agree well with each other (see Fig. 3).
For random regular networks, all the nodes have the same degree k0, and the K-protected core contains the whole network when k0≥K. If a randomly chosen fraction ρ of the links are removed, the degree distribution of the diluted network is given by  with mean degree c=(1–ρ)k0. We predict that
with mean degree c=(1–ρ)k0. We predict that  (for k0=4) and
(for k0=4) and  (for k0=6) at the 2-protected core percolation transition, with c*≈3.08 and c*≈3.37, respectively. These predictions are in full agreement with simulation results (see Fig. 5).
(for k0=6) at the 2-protected core percolation transition, with c*≈3.08 and c*≈3.37, respectively. These predictions are in full agreement with simulation results (see Fig. 5).
Solid and dotted lines are analytic predictions for infinite system. Squares and diamonds are simulation results obtained on a diluted RR network instance with node degree k0=4 and k0=6, respectively, whereas dashed and long-dashed lines are the simulation results obtained on 20 independent diluted network instances of the square and cubic lattice. Each simulated network has N=106 nodes.
We also study the 2-protected core percolation in diluted D-dimensional hypercubic lattice and again find a discontinuous transition. Interestingly, in low dimensions the numerically observed transition point c* is remarkably larger than the theoretical prediction (see Figs 5 and 6). We find that this difference is not a finite-size effect but intrinsic (it remains in the N→∞ limit), and the difference decreases quickly as D increases. The transition point c* fluctuates considerably for low dimensions (especially for D=2,3) and depends considerably on the system size N (for D≤7, see Supplementary Note 8). Moreover, there is no critical scaling behaviour in the supercritical regime (similar absence of critical scaling was also observed in 4-core percolation on D=4 lattices44). Surprisingly, the value of np-core at and after the percolation transition agrees well with our theoretical prediction (see Fig. 5).
Each square is the value of the percolation transition point, c*, obtained for a D-dimensional lattice by averaging over 1,600 independent diluted network instances with N 2 × 106 nodes, diamonds are extrapolated simulation results to N=∞, and circles are analytical predictions of c* for an infinite RR network with vertex degree k0=2D. The differences between the extrapolated simulation results and the theoretical predictions are due to the ignorance of lattice structures in the theory.
2 × 106 nodes, diamonds are extrapolated simulation results to N=∞, and circles are analytical predictions of c* for an infinite RR network with vertex degree k0=2D. The differences between the extrapolated simulation results and the theoretical predictions are due to the ignorance of lattice structures in the theory.
Finally, we apply our theory to a wide range of real-world networks of different sizes and topologies, and find that for most of these networks the normalized sizes of the 2-protected core can be precisely predicted using the degree distribution as the only input (see Supplementary Tables S1 and S2 and Supplementary Note 9).
Discussion
Inducing effect has an important role in many complex networked systems. Yet, little was known about how it will affect classical percolation transitions in complex networks. Here we develop analytical tools to address this problem for arbitrary network topologies. Our key finding, that the local inducing effect causes discontinuous site percolation and K-core percolation (for any K≥1), suggests a simple local mechanism to better understand and ultimately predict many abrupt breakdown phenomena observed in various systems, for example, the global failure of a national-wide power grid, the sudden collapse of a governmental system or a network of financial institutions.
The results presented here also raise a number of questions, answers to which could further deepen our understanding of complex networked systems. First of all, we can improve the local inducing mechanism to be more realistic, for example, by considering that the parameters K and K′ might be different for different nodes, an unprotected node may only be able to induce some particular neighbours (for example, in a directed network), or an unprotected node may recover to the protected state with certain rate and so on. Second, for low-dimensional lattice systems, the lattice structures and the associated short loops cause strong local and long-range correlations among the states of the nodes, which should be properly considered in a future refined theory, for example, by changing the form of Q(k) to include local degree–degree correlations and by exactly computing the effects of short loops up to certain length. Finally, an interesting optimization problem consists of identifying a minimal set of nodes such that perturbing these nodes to the unprotected state will cause the protected core of the whole network to breakdown. In the context of opinion dynamics or viral marketing, this amounts to identifying a minimal set of users for targeted advertisement so that we can dissolve the protected core and eventually all the users will adopt the new opinion or product. We hope our work will stimulate further research efforts on these and other related interesting and challenging questions.
Additional information
How to cite this article: Zhao, J.-H. et al. Inducing effect on the percolation transition in complex networks. Nat. Commun. 4:2412 doi: 10.1038/ncomms3412 (2013).
References
Stauffer, D. & Aharony, A. Introduction to percolation theory 2nd edn CRC Press (1994).
Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Critical phenomena in complex networks. Rev. Mod. Phys. 80, 1275–1335 (2008).
Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. & Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 464, 1025–1028 (2010).
Albert, R., Jeong, H. & Barabási, A.-L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000).
Cohen, R., Erez, K., ben-Avraham, D. & Havlin, S. Resilience of the internet to random breakdowns. Phys. Rev. Lett. 85, 4626–4628 (2000).
Watts, D. J. A simple model of global cascades on random networks. Proc. Natl Acad. Sci. USA 99, 5766–5771 (2002).
Li, W., Bashan, A., Buldyrev, S., Stanley, H. E. & Havlin, S. Cascading failures in interdependent lattice networks: the critical role of the length of dependency links. Phys. Rev. Lett. 108, 228702 (2012).
Pastor-Satorras, R. & Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 86, 3200–3203 (2001).
Kitsak, M. et al. Identification of influential spreaders in complex networks. Nat. Phys. 6, 888–893 (2010).
Gleeson, J. P. High-accuracy approximation of binary-state dynamics on networks. Phys. Rev. Lett. 107, 068701 (2011).
Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Controllability of complex networks. Nature 473, 167–173 (2011).
Liu, Y.-Y., Csóka, E., Zhou, H. J. & Pósfai, M. Core percolation on complex networks. Phys. Rev. Lett. 109, 205703 (2012).
Erdös, P. & Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5, 17–60 (1960).
Callaway, D. S., Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Network robustness and fragility: Percolation on random graphs. Phys. Rev. Lett. 85, 5468–5471 (2000).
Bollobás, B. Random Graphs 2nd edn Cambridge University Press (2001).
Achlioptas, D., D’Souza, R. M. & Spencer, J. Explosive percolation in random networks. Science 323, 1453–1455 (2009).
Riordan, O. & Warnke, L. Explosive percolation is continuous. Science 333, 322–324 (2011).
Nagler, J., Levina, A. & Timme, M. Impact of single links in competitive percolation. Nat. Phys. 7, 265–270 (2011).
Nagler, J., Tiessen, T. & Gutch, H. W. Continuous percolation with discontinuities. Phys. Rev. X 2, 031009 (2012).
Boettcher, S., Singh, V. & Ziff, R. M. Ordinary percolation with discontinuous transitions. Nat. Commun. 3, 787 (2012).
Cho, Y. S., Hwang, S., Herrmann, H. J. & Kahng, B. Avoiding a spanning cluster in percolation models. Science 339, 1185–1187 (2013).
Chalupa, J., Leath, P. L. & Reich, G. R. Bootstrap percolation on a bethe lattice. J. Phys. C: Solid State Phys. 12, L31–L35 (1979).
Pittel, B., Spencer, J. & Wormald, N. Sudden emergence of a giant k-core in a random graph. J. Combin. Theory B 67, 111–151 (1996).
Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. k-core organization of complex networks. Phys. Rev. Lett. 96, 040601 (2006).
Baxter, G. J., Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Bootstrap percolation on complex networks. Phys. Rev. E 82, 011103 (2010).
Karp, R. M. & Sipser, M. Maximum matching in sparse random graphs. InThe 22nd IEEE Annual Symposium on Foundations of Computer Science, 364–375IEEE Computer Society (1981).
Bauer, M. & Golinelli, O. Core percolation in random graphs: a critical phenomena analysis. Eur. Phys. J. B 24, 339–352 (2001).
Mézard, M. & Zecchina, R. The random k-satisfiability problem: from an analytic solution to an efficient algorithm. Phys. Rev. E 66, 056126 (2002).
Parisi, G. On local equilibrium equations for clustering states. arXiv: 0212047v2 (2002).
Seitz, S., Alava, M. & Orponen, P. Focused local search for random 3-satisfiability. J. Stat. Mech. Theor. Exp. P06006 (2005).
Li, K., Ma, H. & Zhou, H. J. From one solution of a 3-satisfiability formula to a solution cluster: frozen variables and entropy. Phys. Rev. E 79, 031102 (2009).
Ritort, F. & Sollich, P. Glassy dynamics of kinetically constrained models. Adv. Phys. 52, 219–342 (2003).
Brummitt, C. D., D’Souza, R. M. & Leicht, E. A. Suppressing cascades of load in interdependent networks. Proc. Natl Acad. Sci. USA 109, E680–E689 (2012).
Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Random graphs with arbitrary degree distributions and their applications. Phys. Rev. E 64, 026118 (2001).
Molloy, M. & Reed, B. A critical point for random graphs with a given degree sequence. Random Struct. Random Struct. Algorithms 6, 161–180 (1995).
Mézard, M. & Montanari, A. Information, Physics, and Computation Oxford Univ. Press (2009).
Zhou, H.-J. Long-range frustration in a spin-glass model of the vertex-cover problem. Phys. Rev. Lett 94, 217203 (2005).
Zhou, H.-J. Erratum: Long-range frustration in a spin-glass model of the vertex-cover problem [Phys. Rev. Lett. 94, 217203 (2005)]. Phys. Rev. Lett 109, 199901 (2012).
Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002).
He, D.-R., Liu, Z.-H. & Wang, B.-H. Complex Systems and Complex Networks Higher Education Press (2009).
Goh, K.-I., Kahng, B. & Kim, D. Universal behavior of load distribution in scale-free networks. Phys. Rev. Lett. 87, 278701 (2001).
Catanzaro, M. & Pastor-Satorras, R. Analytic solution of a static scale-free network model. Eur. Phys. J. B 44, 241–248 (2005).
Lee, J.-S., Goh, K.-I., Kahng, B. & Kim, D. Intrinsic degree-correlations in the static model of scale-free networks. Eur. Phys. J. B 49, 231–238 (2006).
Parisi, G. & Rizzo, T. k-core percolation in four dimensions. Phys. Rev. E 78, 022101 (2008).
Acknowledgements
J.-H.Z. and H.-J.Z. thank Prof. Zhong-Can Ou-Yang for support and Hong-Bo Jin for technical assistance on computer simulation. J.-H.Z. and H.-J.Z. were supported by the National Basic Research Program of China (No. 2013CB932804), the Knowledge Innovation Program of Chinese Academy of Sciences (No. KJCX2-EW-J02) and the National Science Foundation of China (grant Nos. 11121403, 11225526). Y.-Y.L. was supported by the Network Science Collaborative Technology Alliance under Agreement Number W911NF-09-2-0053, the Defense Advanced Research Projects Agency under Agreement Number 11645021, the Defense Threat Reduction Agency-WMD award numbers HDTRA1-08-1-0027 and HDTRA1-10-1-0100, and the generous support of Lockheed Martin.
Author information
Authors and Affiliations
Contributions
H.-J.Z conceived research; H.-J.Z, J.-H.Z and Y.-Y.L performed research; H.-J.Z and Y.-Y.L wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S21, Supplementary Tables S1-S2, Supplementary Notes 1-9 and Supplementary References (PDF 964 kb)
Rights and permissions
About this article
Cite this article
Zhao, JH., Zhou, HJ. & Liu, YY. Inducing effect on the percolation transition in complex networks. Nat Commun 4, 2412 (2013). https://doi.org/10.1038/ncomms3412
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms3412
This article is cited by
-
Topology of products similarity network for market forecasting
Applied Network Science (2019)
-
Spatio-temporal propagation of cascading overload failures in spatially embedded networks
Nature Communications (2016)
-
Contagion on complex networks with persuasion
Scientific Reports (2016)
-
Two Types of Discontinuous Percolation Transitions in Cluster Merging Processes
Scientific Reports (2015)
-
Localized attacks on spatially embedded networks with dependencies
Scientific Reports (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.