Abstract
Dipolar excitons are long-lived quasi-particle excitations in semiconductor heterostructure that carry an electric dipole. Cold dipolar excitons are expected to have new quantum and classical multi-particle correlation regimes, as well as several collective phases, resulting from the intricate interplay between the many-body interactions and their quantum nature. Here we show experimental evidence of a few correlation regimes of a cold dipolar exciton fluid, created optically in a semiconductor bilayer heterostructure. In the higher temperature regime, the average interaction energy between the particles shows a surprising temperature dependence, which is evidence for correlations beyond the mean field model. At a lower temperature, there is a sharp increase in the interaction energy of optically active excitons, accompanied by a strong reduction in their apparent population. This is evidence for a sharp macroscopic transition to a dark state, as has been suggested theoretically.
Similar content being viewed by others
Introduction
Different collective many-body effects in Bose quantum fluids of atoms1 and exciton-polaritons2 have been observed in recent years. The common feature of these quantum fluids is the weak interaction between the particles, which generally can be well described using mean field theories, where the interaction is considered as a local, contact-like scattering1. In contrast, cold dipolar fluids are composed of particles that carry a permanent electric dipole. Owing to the strength and longer range of the dipole–dipole interaction, dipolar fluids are predicted to display physics that goes beyond a mean field description3. In particular, cold dipolar bosons are expected to have new quantum as well as classical multi-particle correlation regimes3,4,5. Observing the many-body correlations will open a window to the complex underlying physics that may drive the fluid into different theoretically proposed collective phases such as dipolar superfluids, dipolar crystals and dipolar liquids6,7,8,9.
There are currently only a few feasible realizations of quantum dipolar fluids that are being experimentally tested. Perhaps the most known are dipolar atoms3 or polar molecules10 in either magneto-optical traps or optical lattices1, and indirect dipolar excitons in semiconductor quantum structures11,12. Indirect dipolar excitons (Xid) are coulomb-bound electron-hole pairs inside an electrically gated semiconductor bilayer (also known as a double quantum well (DQW)). Xid are two-dimensional (2D) boson-like quasi-particles (see illustration in Fig. 1a) with four quasi degenerate spin states (in GaAs based DQW structures). The two states with spin S=±1 are optically active (‘bright’) and the two states with spin S=±2 are optically inactive (‘dark’)13. The Xid carry a static electric dipole because of the separation of the electron and the hole into the two adjacent layers. Furthermore, all the dipoles are aligned perpendicular to the layers, so that the dominant interaction between the Xid is an extended repulsive dipole–dipole interaction14,15. The unique advantage of Xid systems is that the effect of the interactions between the excitons can be observed directly: the interaction of a given exciton with its surrounding excitons is manifested in an excess energy (called the ‘blue shift’ −ΔE), carried away from the system by a photon as the exciton recombines radiatively. It was suggested theoretically that this observed interaction energy could be used as a direct experimental probe of the various particle correlation regimes and the thermodynamic phases of Xid systems5,15, if it can be mapped as a function of the fluid temperature and density16,17. However, calibrating the fluid density reliably at different temperatures turned out to be a non-trivial task in optically excited exciton systems18, which so far hindered direct and consistent observations of interaction-induced particle correlations. On the other hand, recent works have shown other manifestations of a spontaneous transition to a macroscopic condensed state of Xid, such as an extended optical coherence of the Xid emission12,19,20, as well as persistent spin textures12 in excitonic rings21,22.
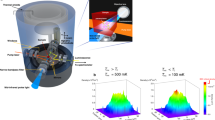
(a) An illustration of the bilayer system, the dipolar excitons and the circular electrostatic trap gate geometry. The excitation laser pulse impinges at the centre of the trap. (b–e) PL of an Xid fluid inside an electrostatic trap at two different times after a non-resonant excitation pulse. The first stage of the dynamics starts with a fast expansion of the dense and hot carriers due to the carrier–carrier repulsion (not seen here), followed by a cooling and a formation of Xid. Owing to their strong dipole–dipole repulsion, these Xid continue to expand rapidly towards the edges of the circular trap26, where they are confined through the interaction of their dipole with the externally applied electric field under the trapping gate. (b,c) Real space images of the Xid fluid PL from an electrostatic trap (b) during the laser pulse and (c) 50 ns after the laser pulse. The PL is spectrally filtered to collect only the emission from the Xid fluid. Note that the Xid fluid reaches a homogeneous distribution in the trap in c. The dashed yellow line mark the trap's gate boundary. (d,e) Spectral colormap images (in log scale) of the Xid PL, taken from the cross-sections of the electrostatic trap, shown by the green dash lines in b,c. The dot-dashed red line marks the spatial location of the excitation spot and the horizontal black lines mark the trap’s gate boundary. The vertical black dot-dashed line marks the energy at the bottom of the trap. The PL is clearly blue shifted with respect to this energy due to mutual dipolar interactions between particles.
In this paper, we show experimental evidence of a few correlation regimes of a cold dipolar exciton fluid, created optically in a semiconductor bilayer heterostructure. In the higher temperature regime, the average interaction energy between the particles shows a temperature dependence that is an evidence for correlations beyond the mean field model. At a lower temperature, there is a sharp increase in the interaction energy of optically active excitons, which is accompanied by a strong reduction in their apparent population. This could be an evidence for a sharp macroscopic transition, where the fluid redistribute its density with dark states that are uncoupled to light, as was suggested theoretically13.
Results
Experimental scheme
Here we present time-resolved photoluminescence (PL) experiments of an optically excited Xid fluid trapped inside an electrostatic trap23,24,25,26. We extract a consistent mapping of ΔE for a range of bright exciton densities (nb) and temperatures. Figure 1b,c show typical time-resolved PL images of an Xid fluid inside an electrostatic trap after its excitation with a non-resonant-pulsed laser. About 50 ns after excitation, the fluid reaches a dynamic equilibrium between the dipole–dipole repulsion of excitons that tends to drive the fluid outwards, and the confining ‘flat well’ potential induced by the electrostatic gate27. This equilibrium results in a uniform and homogeneous PL distribution inside the trap, indicating a flat density profile. This is clearly seen in Fig. 1c,d,e present the corresponding spatial-spectral images taken along the central axis of the trap gate. Figure 1e shows that the homogeneously distributed PL is blue shifted from the emission energy of a single exciton. This positive blue shift energy ΔEid is due to the repulsive dipole–dipole interaction inside the Xid fluid. In general, ΔE increases as nb increases and its value is sensitive to the intricate multi-particle correlation5,15.
Analysis of the Xid lifetime
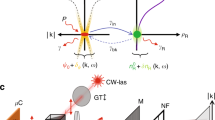
Figure 2a presents an example of the spatially integrated and normalized PL spectra, taken at T=3 K at different times after the excitation pulse. The spectral position of the PL line shifts with time to lower energies as nb decreases. At long times, the PL energy asymptotically reaches a constant value. The difference between the PL energy at any given time to this asymptotic value is the blue shift energy ΔE (marked by the arrow in Fig. 2a). The time dependence of the spectrally integrated PL intensity (I) and ΔE are plotted in Fig. 2b. As the Xid density drops with time, both I and ΔE decreases with a non-exponential decay rate. The reason for this non-exponential decay is the dependence of the Xid radiative recombination time (τid) on nb: as is illustrated in Fig. 3a, radiative recombination of the Xid can be described by a tunelling of either the electron or the hole (with a much lower probability because of its larger mass) to the adjacent well, where direct optical recombination with the oppositely charged particle takes place with a direct exciton recombination time τd. The tunnelling probability depends on the difference between the direct and indirect transition energies, Ed−Eid. The larger the energy difference, the larger the τid compared with τd. This picture can be quantified to get an expression for τid in terms of τd and Ed−Eid (see Supplementary Note 1):
(a) Spatially integrated PL spectra of an Xid fluid in a trap (taken at 3 K) at different times after the short excitation pulse. The intensities are all normalized to unity for convenience. The dot-dashed red line indicates the extrapolated Xid energy as the density of the bright excitons goes to zero. The blue shift energy, ΔE, is measured from this extrapolated energy as is marked by the black arrow. (b) The extracted time dependence ΔE (blue circles) and the integrated intensity I (green squares) from the Xid spectra in a. It is seen that ΔE and I decay non-exponentially and at different rates because of the dependence of the effective Xid lifetime on ΔE (see text). The inset presents the same data as in b but in log scale.
(a) On the left side, a schematic illustration of the energy band diagram of a DQW (in the growth direction) under an applied bias is shown . The energies of the direct exciton (Ed) and the dipolar exciton (Eid) are marked. The right side illustrates the process of an Xid optical recombination in which the electron effectively tunnels to the adjacent well (stage 1) and recombines with the hole (stage 2), emitting a photon. (b) Extracted τid/τd versus time for two experimental temperatures T=1.9 and 5 K, using equation (1). (c) The bright exciton density, nb(t), as a function of time for different temperatures, extracted using the calibration procedure described in the text. (d) The experimentally obtained values of β at different times for three different temperatures. (e) Calculated values of β as a function of nb for the same temperatures as in d using an ideal 2D BE thermal distribution.

where  is the probability for an electron to tunnel to the hole QW, and v is the tunnelling matrix element. Note that although the non-polar, direct transition energy Ed is independent of density, the dipolar energy Eid depends on nb. The time dependence of τid/τd can be extracted from equation (1) by plugging in it the experimental values of Ed−Eid(t). Figure 3b presents this time dependence for the two exemplary temperatures of 1.9 and 5 K.
is the probability for an electron to tunnel to the hole QW, and v is the tunnelling matrix element. Note that although the non-polar, direct transition energy Ed is independent of density, the dipolar energy Eid depends on nb. The time dependence of τid/τd can be extracted from equation (1) by plugging in it the experimental values of Ed−Eid(t). Figure 3b presents this time dependence for the two exemplary temperatures of 1.9 and 5 K.
Density calibration and thermal distribution of the Xid fluid
Because the dominant Xid recombination channel is radiative21,22,28, the dynamics, and its relation to the observed PL intensity, can be described by a simple rate equation. Assuming an equilibrium of bright and dark Xid with equal densities29 (that is, nb=nd, where nd is the dark Xid density), we get:

where nrad is the density of optically active excitons with in-plane k-vectors that are inside the radiation light cone, β≡(nrad/nb), and α(T) is the fraction of the total emitted photon flux that is collected by the detector (see Piermarocchi et al.30 and Supplementary Note 2 for more information). We now note that counting all the emitted photons from a given time t after the excitation to t→∞ (where nb=0) yields nb(t), that is,

Combining equation (2) with equation (3), we get a relation between I(t), τid(t) and β(T):

As τid was extracted independently from the PL energy using equation (1), comparing the two sides of the equation yields β(T,t). This dependence is plotted for three different temperatures in Fig. 3d. β increases with decreasing time, that is, with increasing nb. Also, β decreases with temperature. This density dependence is a signature of a deviation from a pure classical ideal gas distribution. Figure 3e plots the theoretically calculated values of β(nb) for the three corresponding temperatures using an ideal 2D Bose–Einstein (BE) model (see Supplementary Note 2 for the full derivation). There is a reasonable qualitative agreement between the calculation and the experiment, indicating the validity of the model assumptions. However, it is noteworthy that currently we cannot obtain a direct comparison between the theoretical and experimental values of β, as no absolute measurement of nb exists. Another strong verification for the validity of the above analysis was done for a trapped Xid fluid in a steady state under a non-resonant continuous wave laser excitation and is shown in Supplementary Note 3.
Evidence for correlations in the Xid fluid
Figure 4a shows in green circles the temperature dependence of β at the high-density limit (marked by the black dashed lines in Fig. 3d). β(T) increases as T decreases down to ~2.5 K, where it suddenly drops. This behaviour is fitted to an ideal BE distribution, shown by the solid blue line. For temperatures above ~2.5 K, the theoretical prediction fits well with the experimental data. This means that for T 2.5 K, the Xid fluid has a well-defined thermal distribution, but sharply deviates from it at lower temperatures. This is the first important observation of this analysis.
2.5 K, the Xid fluid has a well-defined thermal distribution, but sharply deviates from it at lower temperatures. This is the first important observation of this analysis.
(a) β values at the high exciton density limit (marked by the black dashed lines in Fig. 3d), as a function of T (green circles), the error bars are calculated from the data in Fig. 3d. The solid blue line is the theoretical values of β, assuming an ideal 2D BE thermal distribution with nb=3.5 × 1010 cm−2. (b) ΔE as a function of T for different values of bright exciton densities, nb (dashed lines are guides to the eye). The vertical black dashed line mark Tc, the boundary between the two regimes as is discussed in the text. A lower bound for nb can be obtained from the blue shift at the highest temperature by applying the mean field model5, yielding nb≥2.2 × 1010 cm−2/1 (a.u.). For this density estimate ,we assume that at the highest temperature, the bright and dark exciton densities are identical, and therefore nb is half of the total particle density.
Next, we would like to map the dependence of ΔE on T and nb. This can be done with a common experimental calibration for the optically active exciton densities for all temperatures using equation (3). To do this in a simple tractable manner, we calculate an approximate, density independent value of α(T). We can then use this calculated value with equation (3) and the experimental values of I(t) to get nb(t) for each T. The results are plotted in Fig. 3c. This procedure allows us to compare the behaviour of the Xid fluid with similar densities but at different temperatures.
Figure 4b presents the experimental dependence of ΔE on T for different fixed densities. Two distinct temperature regimes are observed for all densities, corresponding exactly to the two regimes seen for β(T), with a sharp transition between them at Tc 2.5 K. For all temperatures above Tc, a clear temperature dependence of ΔE is observed. ΔE decreases with decreasing T. This dependence is a clear evidence for particle correlations beyond mean field. In contrast, a mean field calculation of ΔE predicts a ‘capacitor formula’ dependence that is temperature independent31. As the dipole–dipole interaction between the excitons is repulsive, a reduction of ΔE for a given density nb means an increase in the particle correlations: the more the Xid spatially correlate to minimize their energy, the smaller ΔE will be. Therefore, the results suggest that as T decreases, the spatial correlations of the excitons in the fluid increase. To better quantify the dependence of ΔE and therefore the particle correlations on nb and T in this regime, we look for a scaling law of our data. Figure 5a plots ΔE for a large set of densities and for all the measured temperatures above, as a function of nbT2. The data collapse into a single linear line to a high accuracy (see inset). The linear dependence of ΔE on nb suggests a lack of long range order in the fluid5. The scaling of ΔE on T2 is surprising. In contrast, the models of Laikhtman and Rapaport, and Schindler and Zimmermann15 predict a much weaker, sublinear dependence of ΔE on T, if the dipoles are a classically correlated gas. This specific temperature dependence could be an indication for a transition of the fluid correlations from classical to quantum. Although the former are expected to lead to a clear temperature dependence of ΔE, the latter should have a much weaker dependence, as was calculated in Laikhtman and Rapaport5. This transition to a temperature independent ΔE is especially clear for the low densities of Fig. 4b, and it happens at a temperature range very similar to the one where quantum degeneracy of Xid was reported very recently12. Lower bound estimation for the Xid density (see caption of Fig. 4b) indeed suggests that the Xid fluid should become quantum degenerate (see Supplementary Fig. S3) for all the densities presented.
2.5 K. For all temperatures above Tc, a clear temperature dependence of ΔE is observed. ΔE decreases with decreasing T. This dependence is a clear evidence for particle correlations beyond mean field. In contrast, a mean field calculation of ΔE predicts a ‘capacitor formula’ dependence that is temperature independent31. As the dipole–dipole interaction between the excitons is repulsive, a reduction of ΔE for a given density nb means an increase in the particle correlations: the more the Xid spatially correlate to minimize their energy, the smaller ΔE will be. Therefore, the results suggest that as T decreases, the spatial correlations of the excitons in the fluid increase. To better quantify the dependence of ΔE and therefore the particle correlations on nb and T in this regime, we look for a scaling law of our data. Figure 5a plots ΔE for a large set of densities and for all the measured temperatures above, as a function of nbT2. The data collapse into a single linear line to a high accuracy (see inset). The linear dependence of ΔE on nb suggests a lack of long range order in the fluid5. The scaling of ΔE on T2 is surprising. In contrast, the models of Laikhtman and Rapaport, and Schindler and Zimmermann15 predict a much weaker, sublinear dependence of ΔE on T, if the dipoles are a classically correlated gas. This specific temperature dependence could be an indication for a transition of the fluid correlations from classical to quantum. Although the former are expected to lead to a clear temperature dependence of ΔE, the latter should have a much weaker dependence, as was calculated in Laikhtman and Rapaport5. This transition to a temperature independent ΔE is especially clear for the low densities of Fig. 4b, and it happens at a temperature range very similar to the one where quantum degeneracy of Xid was reported very recently12. Lower bound estimation for the Xid density (see caption of Fig. 4b) indeed suggests that the Xid fluid should become quantum degenerate (see Supplementary Fig. S3) for all the densities presented.
(a) Scaling of the data of ΔE in Fig. 4b to nbT2 for all T>Tc. The solid straight line was added as a guide to the eye. The inset shows the R2 values of the quality of scaling of the experimental ΔE data to nbδTγ for different values of the exponents γ and δ. (b) The time dependence of the magnitude of the energy ‘jump’ given by δE=Eid(T=2.2 K)−Eid(T=2.6 K), where these two temperatures correspond to the temperatures just below and above Tc, respectively. The dashed red line marks the value of τid(T=2.2 K) at the low density limit.
Evidence for Xid density redistribution in dark states
Turning to the other regime, we observe a sharp increase in ΔE for all densities just below Tc. This jump correlates well with the onset of the deviation from the theoretical values of β plotted in Fig. 4a, where we observe a sharp drop of β(T<Tc) with much less radiative Xid than the theoretical prediction of a BE gas of bright excitons (plotted in blue). In other words, suddenly below Tc, there seem to be less bright excitons but yet more interaction energy. This could be an indication for a sudden and sharp depletion of the bright exciton density and a sudden macroscopic transition to an optically inactive ‘dark’ state below Tc. This increase in the density of the dark state can be seen in ΔE of bright excitons, as these dark excitons still interact with the bright excitons. A BE condensation (BEC) of dark excitons and its effect on the excited bright exciton energy was recently suggested in a theoretical paper by Combescot et al.13 It was proposed that in perfect excitonic systems, the dark excitons should have an energy slightly lower than the bright excitons, and therefore at low enough temperatures and high densities, a BEC should form in the dark state. The following possible scenario is therefore consistent with our experimental observations: for all temperatures, the pulse excitation creates a large density of hot particles that very quickly (within a few nanoseconds) cool down to the lattice temperature. For T>Tc, due to efficient spin flip processes between dark and bright states29,32, their population is approximately equal throughout the optical recombination process and their density decay together with time (that is, nb(t)=nd(t) for all t). At temperatures below Tc, the high-density fluid cools down and condenses fast after excitation, pulling bright excitons to the dark ground state so that the population equality between the two species breaks down, resulting in more dark excitons and less bright excitons than expected (nb<nd), as is seen in Fig. 4a,b. The fact that the temperature dependence of this transition is very sharp (a fraction of a Kelvin), excludes the possibility of a simple thermal re-population of a lower dark state, but rather indicates to a sharp macroscopic transition.
Discussion
With the above picture in mind, it is expected that after the condensation, the scattering between the condensed particles in the fluid will be strongly suppressed, leading to a suppression of spin flip processes and therefore to an effective decoupling of the dark Xid from the bright ones. An evidence for spin-scattering suppression was recently observed and analysed theoretically12. As the condensation and the bright–dark decoupling happens shortly after the pulsed excitation, it should be hard to directly observe the existence of a dark state by monitoring the dynamics of the bright Xid PL intensity alone. However, there is a way to probe the dark state existence, as can be seen from Fig. 5b. Here we plot the time dependence of the energy ‘jump’ given by δE(t)=Eid(t,T=2.2 K)−Eid(t,T=2.6 K), where these two temperatures correspond to the temperatures just below and above Tc respectively. It can be seen that δE persists for times much longer than even the longest bright exciton lifetime (marked by the red dashed line), which indicates that there is a dark long-lived state in the system affecting the energy of the bright Xid via mutual dipolar interactions. This observation is consistent with a dark excitonic state.
A darkening of the PL of Xid in a centre of stress-induced trap was recently observed by Sinclair et al.33 In that work, the observed darkening was successfully explained by a position-dependent mixing of light- and heavy-hole Xid, which have different emission rates. This mixing was induced by the inhomogeneous strain along the trap cross-section, and is essentially a single-particle effect, in contrast to a collective many-body effect. Their explanation could not, however, account for the temperature-dependent onset of their observed darkening. Therefore, it was suggested in Sinclair et al.33 that perhaps many-body effects, and in particular dark–bright exciton splitting and dark exciton BEC, could be also involved; however, these effects could not be isolated. As the same strain fields are also expected to mix bright and dark excitons, it further complicates the interpretation. In our experiments, the trap is electrostatic, with a flat homogeneous electric field distribution all across the trap profile (except at the trap edges), so such mixing of light- and heavy-hole Xid is not seen or expected, yet a significant darkening is observed. Furthermore, here we have a separate account of ΔE, which is proportional to the total Xid density (nb+nd), and of nb alone. This allows us to separate the two types of states and to show that it is really a sharp reduction of emitting particle density and not of the total particle density that occurs across Tc. We are also able to show that the two populations have very different lifetimes, as is expected from a decoupled bright and dark states. It may well be that some of the underlying physics responsible for the observations in Sinclair et al.33 and in the present work are similar. This is an exciting and interesting possibility; however, a direct comparison between the two experiments should be taken with care.
Finally, it may seem from Fig. 4b that Tc is independent of particle density, but this might be misleading: note that in this figure, the different ΔE(T) curves are plotted for fixed nb rather than for the total Xid density. In this plot, for every temperature, the different points of ΔE, which correspond to different nb's, all come from the same experiment (different times after the pulse excitation). As for all T's the initial excitation was the same, it is reasonable that the initial total particle densities were approximately the same. As Tc is expected to depend on the total density right after thermalization (that is, at short times after the excitation), Tc should be fixed by this experimental condition. Therefore, the persistent energy ‘jump’ δE for many values of nb reflects the very long lifetime of the effect, as was explained above.
To summarize, the above results show a few distinct correlation regimes of a 2D dipolar exciton fluid. We note that because of the complexity of the system and the inherent problems of measuring a dark state directly, a consistent theoretical framework that can describe these effects, as well as further experimental efforts, are therefore an outstanding challenge.
Methods
Sample
The sample that is used in the experiment is a bilayer structure consisting of a 120/40/120Å—GaAs/Al0.45Ga0.55As/GaAs DQW on top of a n-doped GaAs substrate grown by molecular beam epitaxy. The bilayer structure consists, which serves as a bottom electrode. A semi-transparent metallic Ti circular electric gate, with a 50-μm diameter, is micro-fabricated on top of the structure and is connected to a top electrode, as illustrated in Fig. 1a. The area of the circular gate forms an electrostatic trap for the Xid34, which remain confined under it. The DQW structure is placed much closer to the bottom electrode than to the top gates in order to prevent a significant charge separation that can occur on the boundary of the trap23,24,35.
Experimental setup
The sample is mounted into a liquid 4He optical cryostat (Janis). The sample temperature in these experiments was varied in the range of 1.3–7 K. The sample is excited non-resonantly with a 671-nm Q-switched laser with a pulse duration of 15 ns and a repetition rate of 25 kHz, focused on the centre of the trap gate. The time and spatially resolved spectral images following the excitation pulses are collected by a fast-gated intensified CCD camera (PIMAX-II) mounted on a spectrometer (Princeton Instruments).
Additional information
How to cite this article: Shilo, Y. et al. Particle correlations and evidence for dark state condensation in a cold dipolar exciton fluid. Nat. Commun. 4:2335 doi: 10.1038/ncomms3335 (2013).
References
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008).
Deng, H., Haug, H. & Yamamoto, Y. Exciton-polariton bose-einstein condensation. Rev. Mod. Phys. 82, 1489–1537 (2010).
Lahaye, T., Menotti, C., Santos, L., Lewenstein, M. & Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 72, 126401 (2009).
Pupillo, G., Micheli, A., Boninsegni, M., Lesanovsky, I. & Zoller, P. Strongly correlated gases of rydberg-dressed atoms: quantum and classical dynamics. Phys. Rev. Lett. 104, 223002 (2010).
Laikhtman, B. & Rapaport, R. Exciton correlations in coupled quantum wells and their luminescence blue shift. Phys. Rev. B 80, 195313 (2009).
Astrakharchik, G. E., Boronat, J., Kurbakov, I. L. & Lozovik, Y. E. Quantum phase transition in a two-dimensional system of dipoles. Phys. Rev. Lett. 98, 060405 (2007).
Büchler, H. P. et al. Strongly correlated 2d quantum phases with cold polar molecules: Controlling the shape of the interaction potential. Phys. Rev. Lett. 98, 060404 (2007).
Böning, J., Filinov, A. & Bonitz, M. Crystallization of an exciton superfluid. Phys. Rev. B 84, 075130 (2011).
Berman, O. L., Kezerashvili, R. Y. & Ziegler, K. Superfluidity of dipole excitons in the presence of band gaps in two-layer graphene. Phys. Rev. B 85, 035418 (2012).
Carr, L. D., DeMille, D., Krems, R. V. & Ye, J. Cold and ultracold molecules: science, technology and applications. New. J. Phys. 11, 055049 (2009).
Eisenstein, J. P. & MacDonald, A. H. Bose-Einstein condensation of excitons in bilayer electron systems. Nature 432, 691–694 (2004).
High, A. A. et al. Spontaneous coherence in a cold exciton gas. Nature 483, 584–588 (2012).
Combescot, M., Betbeder-Matibet, O. & Combescot, R. Bose-einstein condensation in semiconductors: the key role of dark excitons. Phys. Rev. Lett. 99, 176403 (2007).
Lee, R. M., Drummond, N. D. & Needs, R. J. Exciton-exciton interaction and biexciton formation in bilayer systems. Phys. Rev. B 79, 125308 (2009).
Schindler, C. & Zimmermann, R. Analysis of the exciton-exciton interaction in semiconductor quantum wells. Phys. Rev. B 78, 045313 (2008).
Stern, M. et al. Photoluminescence ring formation in coupled quantum wells: excitonic versus ambipolar diffusion. Phys. Rev. Lett. 101, 257402 (2008).
Vörös, Z., Snoke, D. W., Pfeiffer, K. L. & West, K. Direct Measurement of Exciton-Exciton Interaction Energy. Phys. Rev. Lett. 103, 016403 (2009).
Cohen, K., Rapaport, R. & Santos, P. V. Remote dipolar interactions for objective density calibration and flow control of excitonic fluids. Phys. Rev. Lett. 106, 126402 (2011).
High, A. A. et al. Condensation of excitons in a trap. Nano. Lett. 12, 2605–2609 (2012).
Alloing, M., Fuster, D., Gonzalez, Y., Gonzalez, L. & Dubin, F. Observation of macroscopic coherence in self-organized dipolar excitons. Preprint at http://arxiv.org/abs/1210.3176 (2012).
Rapaport, R. et al. Charge separation of dense two-dimensional electron-hole gases: Mechanism for exciton ring pattern formation. Phys. Rev. Lett. 92, 117405 (2004).
Butov, L. V. et al. Formation mechanism and low-temperature instability of exciton rings. Phys. Rev. Lett. 92, 117404 (2004).
Rapaport, R. et al. Electrostatic traps for dipolar excitons. Phys. Rev. B 72, 075428 (2005).
Hammack, A. T. et al. Excitons in electrostatic traps. J. Appl. Phys. 99, 066104 (2006).
Schinner, G. J. et al. Electrostatically trapping indirect excitons in coupled InxGa1−xAs quantum wells. Phys. Rev. B 83, 165308 (2011).
Chen, G. et al. Artificial trapping of a stable high-density dipolar exciton fluid. Phys. Rev. B 74, 045309 (2006).
Rapaport, R., Chen, G. & Simon, S. Analysis of trapped quantum degenerate dipolar excitons. Appl. Phys. Lett. 89, 152118 (2006).
Sivalertporn, K., Mouchliadis, L., Ivanov, A. L., Philp, R. & Muljarov, E. A. Direct and indirect excitons in semiconductor coupled quantum wells in an applied electric field. Phys. Rev. B 85, 045207 (2012).
Maialle, M. Z., De Andrada e Silva, E. A. & Sham, L. J. Exciton spin dynamics in quantum wells. Phys. Rev. B 47, 15776–15788 (1993).
Piermarocchi, C., Tassone, F., Savona, V., Quattropani, A. & Schwendimann, P. Exciton formation rates in GaAs/AlxGa1−xAs quantum wells. Phys. Rev. B 55, 1333–1336 (1997).
Butov, L. V., Shashkin, A. A., Dolgopolov, V. T., Campman, K. L. & Gossard, A. C. Magneto-optics of the spatially separated electron and hole layers in GaAs/AlxGa1−xAs coupled quantum wells. Phys. Rev. B 60, 8753–8758 (1999).
Leonard, J. R. et al. Spin transport of excitons. Nano. Lett. 9, 4204–4208 (2009).
Sinclair, N. W. et al. Strain-induced darkening of trapped excitons in coupled quantum wells at low temperature. Phys. Rev. B 83, 245304 (2011).
Hagn, M., Zrenner, A., Böhm, G. & Weimann, G. Electric-field-induced exciton transport in coupled quantum well structures. Appl. Phys. Lett. 67, 232–234 (1995).
Kowalik-Seidl, K. et al. Tunable photoemission from an excitonic antitrap. Nano. Lett. 12, 326–330 (2012).
Acknowledgements
We would like to thank Oded Agam, Paulo Santos and Snezana Lazic for useful discussions. Y.S., K.C. and R.R. acknowledge funding from the D.F.G. Project no. 581021 and by the Israeli Science Foundation Project no. 1319/12. The work at Princeton was partially funded by the Gordon and Betty Moore Foundation through Grant no. GBMF2719 and by the National Science Foundation MRSEC-DMR-0819860 at the Princeton Center for Complex Materials.
Author information
Authors and Affiliations
Contributions
The experiments were carried out by Y.S. The experimental setup was built by Y.S. and K.C. Y.S. and R.R. analysed the data with a help from K.C. The samples were grown by L.P. and K.W. The expression for the indirect exciton lifetime was derived by B.L. The manuscript was prepared by Y.S. and R.R. with inputs from the other co-authors. R.R. planned and supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S5 and Supplementary Notes 1-3 (PDF 535 kb)
Rights and permissions
About this article
Cite this article
Shilo, Y., Cohen, K., Laikhtman, B. et al. Particle correlations and evidence for dark state condensation in a cold dipolar exciton fluid. Nat Commun 4, 2335 (2013). https://doi.org/10.1038/ncomms3335
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms3335
This article is cited by
-
Non-equilibrium Bose–Einstein condensation in photonic systems
Nature Reviews Physics (2022)
-
Enhanced interactions of interlayer excitons in free-standing heterobilayers
Nature (2022)
-
Confinement of long-lived interlayer excitons in WS2/WSe2 heterostructures
Communications Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.