Abstract
The tunnelling of quasiparticles across Josephson junctions in superconducting quantum circuits is an intrinsic decoherence mechanism for qubit degrees of freedom. Understanding the limits imposed by quasiparticle tunnelling on qubit relaxation and dephasing is of theoretical and experimental interest, particularly as improved understanding of extrinsic mechanisms has allowed crossing the 100 microsecond mark in transmon-type charge qubits. Here, by integrating recent developments in high-fidelity qubit readout and feedback control in circuit quantum electrodynamics, we transform a state-of-the-art transmon into its own real-time charge-parity detector. We directly measure the tunnelling of quasiparticles across the single junction and isolate the contribution of this tunnelling to qubit relaxation and dephasing, without reliance on theory. The millisecond timescales measured demonstrate that quasiparticle tunnelling does not presently bottleneck transmon qubit coherence, leaving room for yet another order of magnitude increase.
Similar content being viewed by others
Introduction
Quasiparticle (QP) excitations adversely affect the performance of superconducting devices in a wide range of applications. They limit the sensitivity of photon detectors in astronomy1,2, the accuracy of current sources in metrology3, the cooling power of micro-refrigerators4 and could break the topological protection of Majorana qubits5. In superconducting quantum information processing (QIP), the preservation of charge parity (even or odd number of electrons) has historically been a primary concern. In the first superconducting qubit, termed the Cooper-pair box (CPB)6, maintaining the parity in a small island connected to a reservoir via Josephson junctions is essential to qubit operation. The qubit states |0〉 and |1〉 consist of symmetric superpositions of charge states of equal parity, brought into resonance by a controlled charge bias ng and split by the Josephson tunnelling energy EJ (≲EC, the island Cooper-pair charging energy). QP tunnelling across the junction changes the island parity, ‘poisoning’ the box until parity switches back or ng is offset by ±e (ref. 7). QP poisoning has been extensively studied in CPBs and similar devices, such as single-Cooper-pair transistors and charge pumps, with most experiments8,9,10,11,12,13 finding parity switching times of 10 μs–1 ms, and some >1 s (refs 14, 15, 16). While these times are long compared with qubit gate operations (∼10 ns), the sensitivity of the CPB qubit transition frequency ω01 to background charge fluctuations limits the dephasing time to <1 μs, severely restricting the use of traditional CPBs in QIP.
Engineering the CPB into the transmon regime EJ≫EC (refs 17, 18) exponentially suppresses the sensitivity of ω01 to charge-parity and background charge fluctuations. However, recent theory19,20,21 predicts that QP tunnelling remains a relevant source of relaxation and pure dephasing of the qubit degree of freedom. The contribution of QP tunnelling on qubit decoherence has become particularly interesting as control of the Purcell effect22 in circuit quantum electrodynamics (cQED)23 and the reduced contribution of dielectric losses in three-dimensional geometries24 have allowed reaching the 100 μs scale. To guide further improvements, it is imperative to precisely pinpoint the timescale for QP tunnelling and its contribution to qubit decoherence. To date, only upper and lower bounds on QP tunnelling rates have been placed18,25 in transmon qubits, while the effect of QP tunnelling on transmon decoherence remains unexplored.
Here, we transform a state-of-the-art single-junction transmon qubit into a real-time charge-parity detector. We measure both the characteristic time for QP tunnelling across the junction and the effect of such tunnelling on qubit decoherence at the millisecond timescale. Our qubit is controlled and measured in a three-dimensional cQED architecture24, an emerging platform for QIP, without need for any electrometer or other circuitry. At the heart of our detection scheme is a very small but detectable parity dependence of the qubit transition frequency (up to 0.04% of the average ω01/2π=4.387 GHz), obtained by choosing EJ/EC=25.
Results
Evidence of QP tunnelling
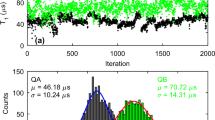
Standard Ramsey fringe experiments provide the first evidence of QP tunnelling across the qubit junction, as shown in Fig. 1 for a refrigerator temperature Tr=20 mK. Instead of the usual single decaying sinusoid, we observe two. Repeated Ramsey experiments always reveal two frequencies, fluctuating symmetrically about the average ω01 (Fig. 1c). The double frequency pattern results from QP tunnelling events causing ng to shift by ±e. The fluctuation in the difference Δf between the two frequencies is owing to background charge motion slow compared with QP tunnelling. The observation of two frequencies in every experiment shows that QP tunnelling is fast compared with the averaging time (∼15 s), but slow compared with the maximum time 1/2Δf∼5 μs (ref. 26). From the similar amplitude of the sinusoids, we can already deduce that the two parities are equally likely. Clearly, these time-averaged measurements only loosely bound the timescale for QP tunnelling, similarly to refs 18, 25.
(a) Ramsey fringe experiment (dots) and best-fit sum of two decaying sinusoids (curve). The reference oscillator is detuned 1 MHz from the average qubit transition frequency ω01/2π=4.387 GHz. (b) Sketch of the charge dispersion of the two lowest-energy levels of the transmon qubit, showing 2e periodicity. QP tunnelling across the junction shifts ng by ±e, resulting in two transition frequencies fe and fo (not to scale). (c) Repeated Ramsey experiments (15 s each) show a symmetric drift of fe and fo around ω01/2π, arising from background charge motion. The frequency difference 2Δf=fe−fo ranges from 0 to 1.76 MHz (see also Supplementary Fig. S1).
Real-time detection of charge-parity fluctuations
In order to accurately pinpoint the timescale for QP tunnelling, we have devised a scheme to monitor the charge parity in real time using the qubit itself (Fig. 2a). The scheme takes advantage of recent developments in high-fidelity nondemolition readout27,28 and feedback control29. Starting from |0〉, the qubit is prepared in the superposition state ( with a π/2 y-pulse at ω01. The Rabi frequency of 16 MHz is sufficient to drive both odd- and even-parity qubit transitions, which differ by 2Δf ≤1.76 MHz. The qubit then acquires a phase ±π/2 during a chosen idle time Δt=1/4Δf, where the + (−) sign corresponds to even (odd) parity. A second π/2 x-pulse completes the mapping of parity into a qubit basis state, even →|0〉, odd →|1〉. A following projective qubit measurement ideally matches the result P=1 (−1) to even (odd) parity. Feedback-based reset29 reinitializes the qubit to |0〉 and allows repeating this sequence every Δtexp=6 μs.
with a π/2 y-pulse at ω01. The Rabi frequency of 16 MHz is sufficient to drive both odd- and even-parity qubit transitions, which differ by 2Δf ≤1.76 MHz. The qubit then acquires a phase ±π/2 during a chosen idle time Δt=1/4Δf, where the + (−) sign corresponds to even (odd) parity. A second π/2 x-pulse completes the mapping of parity into a qubit basis state, even →|0〉, odd →|1〉. A following projective qubit measurement ideally matches the result P=1 (−1) to even (odd) parity. Feedback-based reset29 reinitializes the qubit to |0〉 and allows repeating this sequence every Δtexp=6 μs.
(a) Ramsey-type sequence converting the qubit into a charge-parity detector. The sequence (see main text) is equivalent to a qubit flip conditioned on odd charge parity. (b) Snapshot (10 ms) of a typical measurement trace, 48 ms long, at Tr=20 mK. Dots are repetitions of the experiment in a, at 6 μs interval. Inset: 1 ms zoom in, with indicated dwell times t+1 and t−1 for P=±1. (c) Double-sided power spectral density of P, obtained by averaging the squared Fourier transform of 45 consecutive repetitions of (b). The best fit of equation (1) gives the QP tunnelling characteristic time 1/Γrts=0.794±0.005 ms and the overall detection fidelity F=0.918±0.002. Repeated experiments have a s.d. of 0.09 and 0.03 ms, respectively. (d) Histograms of t+1 and t−1. The grey curve is a model of RTS, with Γrts and F extracted from the fit in the main panel. (e) Optical image of a qubit with identical geometry28 to that used. See Methods and Supplementary Figs S2–S4 for several control experiments testing the measurement protocol.
The time evolution of charge parity is encoded in the series of results P (Fig. 2b). The time series has zero average, confirming that the two charge parities are equally probable. Both the QP dynamics and the detection infidelity determine the distribution of dwell times t+1 and t−1 (Fig. 2d). The measured identical histograms match a numerical simulation of a symmetric random telegraph signal (RTS) with transition rate Γrts, masked by uncorrelated detection errors occurring with probability (1−F)/2. These two noise processes contribute distinct signatures to the spectral density of P (Fig. 2c). The best fit of the form

shows excellent agreement, giving 1/Γrts=0.79 ms and F=0.92.
Measurement of QP-tunnelling-induced qubit decoherence
While the above scheme detects a characteristic time for QP tunnelling, our goal is to determine the effect of such QP tunnelling on the performance of the qubit degree of freedom. Specifically, we aim to determine the rates  connecting level |kl〉 to level |k′l′〉 (k (k′) and l (l′) denote the initial (final) qubit and parity state, respectively, as illustrated in Fig. 3b). For example,
connecting level |kl〉 to level |k′l′〉 (k (k′) and l (l′) denote the initial (final) qubit and parity state, respectively, as illustrated in Fig. 3b). For example,  denotes the QP-tunnelling-induced qubit relaxation rate. Based on the identical distribution of dwell times, we safely approximate symmetric rates
denotes the QP-tunnelling-induced qubit relaxation rate. Based on the identical distribution of dwell times, we safely approximate symmetric rates  .
.
(a) Pulse sequence measuring the autocorrelation function of charge parity. Two charge-parity sequences, ending with measurements P1 and P2, respectively, are separated by a variable delay, followed by a qubit measurement M. We indicate by τ the time between the end of P1 and the start of M. Postselection on P1=+1 (ref. 28) prepares the state |0e〉. Similarly, a measurement M=+1 ensures that the final qubit state is |0〉. P2 will coincide with P1 only if the parity is unchanged. Inserting π rotations after P1 and/or before M allows measuring the parity autocorrelation for different combinations of qubit states. A preliminary measurement (not shown) initializes the qubit in |0〉 by postselection. Note that every measurement is projective on the qubit state. When the initial qubit state is known and the measurement is preceded by the parity-controlled qubit flip (Fig. 2), the result also denotes the charge parity. (b) Diagram of the four energy levels with the modelled transition rates (not to scale). (c) Charge-parity autocorrelation Rkk′(τ) for qubit in state |0〉 (dots), |1〉 (squares), or having relaxed from |1〉 to |0〉 (diamonds) during τ (Tr=20 mK). The average of the conditioned P2 is corrected for detection infidelity (see Methods). Fitting the solution of the rate equations, conditioned on initial and final qubit states, gives the inverse rates:  ,
,  ,
,  ,
,  .
.
To extract the above rates, we measure the autocorrelation function of charge parity, conditioned on specific initial and final qubit states (Fig. 3). We first execute the charge-parity sequence illustrated in Fig. 2. Conditioning on the result of the projective measurement P1=+1 postselects the qubit in |0〉 and even parity. After a waiting time τ, another measurement M determines the qubit state. Conditioning also on M=+1 ensures that the qubit ends in |0〉. A second instance of the charge-parity sequence, ending with P2, completes the scheme. The average result, once corrected for detector infidelity (see Methods), is the parity autocorrelation R00(τ)=〈P(0)P(τ)〉00, with first (second) subscript indicating initial (final) qubit state. Neglecting qubit excitation, that is, setting  , R00(τ) simply decays as
, R00(τ) simply decays as  . The exact solution shows that this remains a valid approximation when including the measured Γ01=1/6 ms−1, as the probability of multiple qubit transitions in τ is negligible. Similarly, we measure the parity autocorrelation with qubit initially and finally in |1〉,
. The exact solution shows that this remains a valid approximation when including the measured Γ01=1/6 ms−1, as the probability of multiple qubit transitions in τ is negligible. Similarly, we measure the parity autocorrelation with qubit initially and finally in |1〉,  . To do this, we use the same conditioning, but apply a π pulse after P1 and before M. Exponential decay fits give
. To do this, we use the same conditioning, but apply a π pulse after P1 and before M. Exponential decay fits give  and
and  .
.
To quantify the contribution of QP tunnelling to the measured net qubit relaxation time T1=1/Γ10=0.14±0.01 ms (see Methods), we apply the same method, but condition on initial state |1〉 and final state |0〉. The ratio of QP-induced to total relaxation rates  can be extracted from R10(τ→0)=1−2α. The best fit of the model R10(τ) to the data, with α as only free parameter, gives
can be extracted from R10(τ→0)=1−2α. The best fit of the model R10(τ) to the data, with α as only free parameter, gives  and
and  . This result clearly demonstrates that QP tunnelling does not dominate qubit relaxation at Tr=20 mK, contributing only 5% of qubit relaxation events.
. This result clearly demonstrates that QP tunnelling does not dominate qubit relaxation at Tr=20 mK, contributing only 5% of qubit relaxation events.
To facilitate comparison of the measured rates to theory, we perform the above experiments at elevated Tr (Fig. 4). We observe that  ,
,  and
and  have similar magnitude and jointly increase with Tr in the range 20–170 mK. However, T1 remains insensitive to Tr until 150 mK. The observed sign reversal in R10(τ→0) near this temperature (Fig. 4b) indicates that QP tunnelling becomes the dominant qubit relaxation process.
have similar magnitude and jointly increase with Tr in the range 20–170 mK. However, T1 remains insensitive to Tr until 150 mK. The observed sign reversal in R10(τ→0) near this temperature (Fig. 4b) indicates that QP tunnelling becomes the dominant qubit relaxation process.
(a,b) Charge-parity autocorrelation functions R00(τ) and R10(τ) at 20,80 (a), 150 and 170 mK (b). R10(τ→0) progressively decreases, indicating an increasing contribution of QP tunnelling to qubit relaxation. (c) Relaxation times with ( , upward triangles) and without (
, upward triangles) and without ( , downward triangles) QP tunnelling, obtained from R10(τ). Dashed curve: equation (2) for thermal equilibrium. (d) Times for QP tunnelling times without qubit relaxation in the ground-state (
, downward triangles) QP tunnelling, obtained from R10(τ). Dashed curve: equation (2) for thermal equilibrium. (d) Times for QP tunnelling times without qubit relaxation in the ground-state ( , dots) and excited-state (
, dots) and excited-state ( , squares) manifold extracted from R00(τ) and R11(τ) (not shown). Dashed curve: theory for
, squares) manifold extracted from R00(τ) and R11(τ) (not shown). Dashed curve: theory for  (refs 19, 21) for thermally distributed QPs and Δ=170 μeV. Error bars are 1 s.d. See Supplementary Fig. S5 for the temperature dependence of Γrts.
(refs 19, 21) for thermally distributed QPs and Δ=170 μeV. Error bars are 1 s.d. See Supplementary Fig. S5 for the temperature dependence of Γrts.
Discussion
The effect of QP dynamics on the qubit degree of freedom in superconducting circuits has been extensively studied theoretically7,19,20,21. For transmon qubits, the predicted QP-induced relaxation rate is19,20

where xqp=nqp/2ν0Δ is the QP density nqp normalized to the Cooper-pair density, with ν0=1.2 × 104 μm−3μeV−1 the single-spin density of states at the Fermi energy11 and Δ the Al superconducting gap. This relation holds for any energy distribution of QPs. For Tr≥150 mK, the data closely match equation (2) using the thermal equilibrium  and Δ=170 μeV, the value estimated from the normal-state resistance of the junction (see Methods). The suppression of
and Δ=170 μeV, the value estimated from the normal-state resistance of the junction (see Methods). The suppression of  at lower Tr is much weaker than expected from a thermal QP distribution. Using equation (2), we estimate nqp=0.04±0.01 μm−3 at Tr=20 mK, matching the lowest value reported for Al in a Cooper-pair transistor for use in metrology30. Improved shielding against infrared radiation31 could further decrease nqp at low Tr, consequently suppressing the contribution of QP tunnelling to qubit relaxation, and will be pursued in future work.
at lower Tr is much weaker than expected from a thermal QP distribution. Using equation (2), we estimate nqp=0.04±0.01 μm−3 at Tr=20 mK, matching the lowest value reported for Al in a Cooper-pair transistor for use in metrology30. Improved shielding against infrared radiation31 could further decrease nqp at low Tr, consequently suppressing the contribution of QP tunnelling to qubit relaxation, and will be pursued in future work.
QP tunnelling events that do not induce qubit transitions still contribute to pure qubit dephasing. Calculations based on refs 19, 21 predict  , in good agreement with the data (Fig. 4c). It is presently not understood whether such QP tunnelling events completely destroy qubit superposition states (case A) or simply change the qubit precession frequency (case B). In either case, in the regime of strongly coupled RTS valid for our experiment (
, in good agreement with the data (Fig. 4c). It is presently not understood whether such QP tunnelling events completely destroy qubit superposition states (case A) or simply change the qubit precession frequency (case B). In either case, in the regime of strongly coupled RTS valid for our experiment ( (ref. 26)) the QP-induced dephasing time is
(ref. 26)) the QP-induced dephasing time is  . For case B, this time would further increase in the weak-coupling regime (attained at EJ/EC≳60) owing to motional averaging26.
. For case B, this time would further increase in the weak-coupling regime (attained at EJ/EC≳60) owing to motional averaging26.
In conclusion, we have converted a state-of-the-art transmon qubit into its own charge-parity detector to answer whether QP tunnelling already limits qubit coherence. We measure the contribution of QP tunnelling to relaxation and dephasing to be in the millisecond range. We stress that these times are directly measured, without relying on any theory. Thus, transmon qubit coherence can increase by at least another order of magnitude before QP tunnelling begins to limit coherence. Such an increase would facilitate the realization of fault-tolerant quantum computing in the solid state. The implemented scheme also provides an essential ingredient in the envisioned top-transmon architecture for manipulation and readout of Majorana qubits32.
Methods
Device parameters
The transmon has Josephson energy EJ=8.442 GHz and charging energy EC=0.334 GHz. Using the Ambegaokar–Baratoff relation EJRn=Δ/8e2 and the measured room-temperature resistance Rn,300K=15.2 kΩ of the single Josephson junction, we estimate Δ=170 μeV. The qubit couples to the cavity fundamental mode ωr/2π=6.551 GHz (decay rate κ/2π=720 kHz) with strength g/2π=66 MHz, inducing a dispersive shift χ/π=−1.0 MHz. The qubit relaxation time T1 may be limited by the multi-mode Purcell effect22. A simple estimate including only the fundamental mode gives 240 μs. The dephasing time,  μs, is limited by background charge fluctuations (see Supplementary Fig. S1).
μs, is limited by background charge fluctuations (see Supplementary Fig. S1).
Experimental setup
The device and the experimental setup are similar to those described in refs 28, 29. Here, we detail the changes we made since these earlier reports. In an effort to lower the transmon residual excitation, we replaced the Al cavity with a Cu cavity33, improved thermal anchoring to the mixing chamber plate and added low-pass filters (K&L Microwave 6L250-8000/T18000-O/O) on the input and output ports of the cavity. As a result, the transmon effective temperature decreased from 127 to 55 mK, corresponding to a reduction of total steady-state excitation from ∼16 to 2%, respectively. As these changes were made simultaneously, we cannot pinpoint the individual contributions to the improved thermalization.Projective readout with 99% fidelity is achieved by homodyne detection with a 400 ns pulse at ωr−χ, aided by a Josephson parametric amplifier28. To perform qubit reset faster, we replaced the ADwin processor with a home-built feedback controller based on a complex programmable logic device (CPLD, Altera MAX V). The CPLD integrates the last 200 ns of the readout signal and conditionally triggers a π pulse (all resonant pulses are Gaussian, with σ=8 ns, and total duration 32 ns). The CPLD allows a response time, from the end of signal integration to the π-pulse trigger, of 0.11 μs. The total loop time, from the start of the measurement pulse to the end of the triggered π pulse at the cavity input, is 0.98 μs. However, a delay is added to reach 2 μs (∼10/κ) between the end of measurement and the start of the conditioned π pulse, ensuring that the cavity is devoid of readout photons.
Extraction of QP tunnelling rates
To convert 〈P2(τ)〉kk′ into Rkk′(τ), we correct for the overall detection errors, distributed among readout (<1%) and reset (∼1%) infidelities, suboptimal Δt (<2%) and dephasing during Δt (remaining 1−3%). For this correction, we first fit an exponential decay to 〈P2(τ)〉00 and 〈P2(τ)〉11. The average of the best-fit value at τ=0 is used to renormalize the data in Figs 3c and 4a. The fitted decay times are  and
and  , respectively. To extract
, respectively. To extract  and
and  , we fit the solution of equation (2) to R10(τ), using
, we fit the solution of equation (2) to R10(τ), using  . Γ10 is obtained from the equilibration time Teq after inverting the steady-state populations P|0〉,ss, P|1〉,ss with a π pulse:
. Γ10 is obtained from the equilibration time Teq after inverting the steady-state populations P|0〉,ss, P|1〉,ss with a π pulse:

The total excitation 1−P|0〉,ss is obtained by measurement and postselection29. Equation (3) remains a valid approximation even for the highest temperatures in Fig. 4, at which population of higher excited states becomes relevant. In this case, the populations P|0〉,ss, P|1〉,ss are estimated from the total excitation, assuming that the populations are thermally distributed29. Error bars for  are calculated from the s.d. of repeated T1 measurements and the fit uncertainty in α.
are calculated from the s.d. of repeated T1 measurements and the fit uncertainty in α.
Validation of the charge-parity detector
We perform several control experiments to validate the use of the qubit as a charge-parity detector. First, the parity to qubit-state conversion is tested with suboptimal choices of the Ramsey interval Δt (Supplementary Fig. S2). As expected from equation (1), the white noise level in SP increases at the expense of the signal contrast as Δt deviates from the optimal choice 1/4Δf. Remarkably, the extracted rate Γrts is approximately constant down to F∼0.4. This is consistent with the model of charge parity as a symmetric RTS, with time constant determined solely by QP tunnelling.In a second test, we replace the Ramsey-like sequence with a single pulse, with rotation angle θ. Time series of M for θ=0, π and π/2 are shown in Supplementary Fig. S3a. The very high occurrence (∼99%) of 1 (−1) for θ=0 (π) equals the efficiency of reset, following each measurement M. For θ=π/2, the qubit is repeatedly prepared in an equal superposition of |0〉 and |1〉, and the measurement produces uncorrelated projection noise. The spectra of these control experiments are compared with the QP tunnelling measurement in Supplementary Fig. S3b, clearly showing that the observed RTS is owing to the signal acquired during Δt.As a final test of the charge-parity detector, we subject the qubit to an externally generated RTS, similar to ref. 25. Symmetric RTS sequences with switching rate Γπ are generated in LabVIEW and sent to an ADwin controller. The ADwin samples the RTS at 9 μs interval. When the signal is +1, the ADwin triggers an AWG520 (also used for reset29), which then applies a π pulse on the qubit. As a result, the measured qubit state in M is conditioned on the RTS state, mimicking the parity-controlled π pulse implemented in Fig. 2. In all cases, the fitted rates Γfit match the programmed Γπ within 3% (Supplementary Fig. S4).
Additional information
How to cite this article: Ristè, D. et al. Millisecond charge-parity fluctuations and induced decoherence in a superconducting transmon qubit. Nat. Commun. 4:1913 doi: 10.1038/ncomms2936 (2013).
References
Day, P. K., LeDuc, H. G., Mazin, B. A., Vayonakis, A. & Zmuidzinas, J. A broadband superconducting detector suitable for use in large arrays. Nature 425, 817–821 (2003).
Stone, K. J. et al. Real time quasiparticle tunneling measurements on an illuminated quantum capacitance detector. Appl. Phys. Lett. 100, 263509 (2012).
Pekola, J. P. et al. Single-electron current sources: towards a refined definition of ampere. Preprint at http://arXiv.org/abs/1208.4030 (2012).
Giazotto, F., Heikkilä, T. T., Luukanen, A., Savin, A. M. & Pekola, J. P. Opportunities for mesoscopics in thermometry and refrigeration: physics and applications. Rev. Mod. Phys. 78, 217–274 (2006).
Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Bouchiat, V., Vion, D., Joyez, P., Esteve, D. & Devoret, M. H. Quantum coherence with a single Cooper pair. Phys. Scr. T76, 165–170 (1998).
Lutchyn, R. M., Glazman, L. I. & Larkin, A. I. Kinetics of the superconducting charge qubit in the presence of a quasiparticle. Phys. Rev. B 74, 064515 (2006).
Aumentado, J., Keller, M. W. & Martinis, J. M. A seven-junction Cooper pair pump. Physica E 18, 37–38 (2003).
Ferguson, A. J., Court, N. A., Hudson, F. E. & Clark, R. G. Microsecond resolution of quasiparticle tunneling in the single-Cooper-pair transistor. Phys. Rev. Lett. 97, 106603 (2006).
Naaman, O. & Aumentado, J. Time-domain measurements of quasiparticle tunneling rates in a single-Cooper-pair transistor. Phys. Rev. B 73, 172504 (2006).
Court, N. A., Ferguson, A. J., Lutchyn, R. & Clark, R. G. Quantitative study of quasiparticle traps using the single-Cooper-pair transistor. Phys. Rev. B 77, 100501 (2008).
Shaw, M. D., Lutchyn, R. M., Delsing, P. & Echternach, P. M. Kinetics of nonequilibrium quasiparticle tunneling in superconducting charge qubits. Phys. Rev. B 78, 024503 (2008).
Lenander, M. et al. Measurement of energy decay in superconducting qubits from nonequilibrium quasiparticles. Phys. Rev. B 84, 024501 (2011).
Tuominen, M. T., Hergenrother, J. M., Tighe, T. S. & Tinkham, M. Experimental evidence for parity-based 2e periodicity in a superconducting single-electron tunneling transistor. Phys. Rev. Lett. 69, 1997–2000 (1992).
Eiles, T. M. & Martinis, J. M. Combined Josephson and charging behavior of the supercurrent in the superconducting single-electron transistor. Phys. Rev. B 50, 627–630 (1994).
Amar, A., Song, D., Lobb, C. J. & Wellstood, F. C. 2e to e periodic pair currents in superconducting Coulomb-blockade electrometers. Phys. Rev. Lett. 72, 3234–3237 (1994).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Schreier, J. A. et al. Suppressing charge noise decoherence in superconducting charge qubits. Phys. Rev. B 77, 180502 (2008).
Martinis, J. M., Ansmann, M. & Aumentado, J. Energy decay in superconducting Josephson-junction qubits from nonequilibrium quasiparticle excitations. Phys. Rev. Lett. 103, 097002 (2009).
Catelani, G., Schoelkopf, R. J., Devoret, M. H. & Glazman, L. I. Relaxation and frequency shifts induced by quasiparticles in superconducting qubits. Phys. Rev. B 84, 064517 (2011).
Catelani, G., Nigg, S. E., Girvin, S. M., Schoelkopf, R. J. & Glazman, L. I. Decoherence of superconducting qubits caused by quasiparticle tunneling. Phys. Rev. B 86, 184514 (2012).
Houck, A. A. et al. Controlling the spontaneous emission of a superconducting transmon qubit. Phys. Rev. Lett. 101, 080502 (2008).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
Paik, H. et al. Observation of high coherence in Josephson junction qubits measured in a three-dimensional circuit QED architecture. Phys. Rev. Lett. 107, 240501 (2011).
Sun, L. et al. Measurements of quasiparticle tunneling dynamics in a band-gap-engineered transmon qubit. Phys. Rev. Lett. 108, 230509 (2012).
Paladino, E., Faoro, L., Falci, G. & Fazio, R. Decoherence and 1/f noise in Josephson qubits. Phys. Rev. Lett. 88, 228304 (2002).
Johnson, J. E. et al. Heralded state preparation in a superconducting qubit. Phys. Rev. Lett. 109, 050506 (2012).
Ristè, D., van Leeuwen, J. G., Ku, H.-S., Lehnert, K. W. & DiCarlo, L. Initialization by measurement of a superconducting quantum bit circuit. Phys. Rev. Lett. 109, 050507 (2012).
Ristè, D., Bultink, C. C., Lehnert, K. W. & DiCarlo, L. Feedback control of a solid-state qubit using high-fidelity projective measurement. Phys. Rev. Lett. 109, 240502 (2012).
Saira, O. -P., Kemppinen, A., Maisi, V. F. & Pekola, J. P. Vanishing quasiparticle density in a hybrid Al/Cu/Al single-electron transistor. Phys. Rev. B 85, 012504 (2012).
Barends, R. et al. Minimizing quasiparticle generation from stray infrared light in superconducting quantum circuits. Appl. Phys. Lett. 99, 113507 (2011).
Hassler, F., Akhmerov, A. R. & Beenakker, C. W. J. The top-transmon: a hybrid superconducting qubit for parity-protected quantum computation. New J. Phys. 13, 095004 (2011).
Rigetti, C. et al. Superconducting qubit in a waveguide cavity with a coherence time approaching 0.1 ms. Phys. Rev. B 86, 100506 (2012).
Acknowledgements
We thank G. Catelani, A. Endo, F. Hassler, G. de Lange, J. M. Martinis, O. -P. Saira, L. M. K. Vandersypen, P. J. de Visser and the Yale cQED team for discussions. We acknowledge funding from the Dutch Organization for Fundamental Research on Matter (FOM), the Netherlands Organization for Scientific Research (NWO, VIDI scheme), the EU FP7 project SOLID and the DARPA QuEST program.
Author information
Authors and Affiliations
Contributions
D.R. fabricated the device, M.J.T. and R.N.S. realized the feedback controller, K.W.L. designed the Josephson parametric amplifier, D.R. and C.C.B. performed the experiment and data analysis, D.R. and L.D.C. wrote the manuscript, and L.D.C. designed and supervised the experiment.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S5 (PDF 647 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Ristè, D., Bultink, C., Tiggelman, M. et al. Millisecond charge-parity fluctuations and induced decoherence in a superconducting transmon qubit. Nat Commun 4, 1913 (2013). https://doi.org/10.1038/ncomms2936
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2936
This article is cited by
-
Superconducting tunnel junctions with layered superconductors
Quantum Frontiers (2024)
-
Two-level system hyperpolarization using a quantum Szilard engine
Nature Physics (2023)
-
Thermalization and dynamics of high-energy quasiparticles in a superconducting nanowire
Nature Physics (2023)
-
A Review of Developments in Superconducting Quantum Processors
Journal of the Indian Institute of Science (2023)
-
Engineering superconducting qubits to reduce quasiparticles and charge noise
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.