Abstract
Fossil amber offers the opportunity to investigate the dynamics of glass-forming materials far below the nominal glass transition temperature. This is important in the context of classical theory, as well as some new theories that challenge the idea of an ‘ideal’ glass transition. Here we report results from calorimetric and stress relaxation experiments using a 20-million-year-old Dominican amber. By performing the stress relaxation experiments in a step-wise fashion, we measured the relaxation time at each temperature and, above the fictive temperature of this 20-million-year-old glass, this is an upper bound to the equilibrium relaxation time. The results deviate dramatically from the expectation of classical theory and are consistent with some modern ideas, in which the diverging timescale signature of complex fluids disappears below the glass transition temperature.
Similar content being viewed by others
Introduction
P.W. Anderson said in 1995 ‘The deepest and most interesting unsolved problem in solid state theory is probably the theory of the nature of glass and the glass transition.1’ This remains to be true and in the present work, we use measurements of the calorimetric and dynamic properties of an extremely stable fossil amber glass to provide new insights into the fundamentals of the nature of glass-forming materials.
Vogel–Fulcher–Tammann (VFT)2,3,4 behaviour is a classic signature of glass-forming or complex systems, and describes their equilibrium dynamics as following a super-Arrhenius behaviour that diverges at a finite temperature5,6. However, classic models7,8 and some modern models9 that predict such VFT-like behaviour have been challenged by new evidence from both theoretical10,11,12,13,14 and experimental15,16,17,18,19,20,21,22 works, which contradict such a finite temperature divergence. The difficulty of directly addressing the VFT behaviour experimentally arises owing to the ‘geological’ ages23 required to attain equilibrium far below the glass transition temperature Tg. Prior direct15,16,17,18 interrogation of the equilibrium dynamics was limited to <16 °C below the Tg.
The VFT function describes the temperature dependence of material viscosity η or relaxation time τ:

where η0, τ0, B and T∞ are material-dependent constants. T∞ defines the divergent point for the viscosity or relaxation time and is often related to the Kauzmann temperature24, which is thought to be related to the ‘ideal’ glass temperature25.
Determining the equilibrium behaviour of a glass-forming system far below the conventional glass transition temperature has been a problem that dates at least since the time of Kauzmann24 owing to the fact that the relaxation times grow extremely rapidly as the temperature is lowered—the previously referred to ‘geologic’ age problem23. While there has been some work to try to investigate the thermodynamics via extrapolation methods26, the dynamics remain elusive. The traditional method of addressing the sub-Tg dynamics is to quench a sample from above Tg to the temperature of interest and age it isothermally until it reaches equilibrium.15,16,17,18 Then the equilibrium relaxation time can be determined as a function of temperature. However, this kind of measurement cannot obtain data far below Tg owing to the (apparently) super-Arrhenius increase in times for the non-equilibrium glass to age into equilibrium, for example, 12 days for the mechanical response 8 K below the Tg16.
In the present work, an extremely stable (20 million year) Dominican fossil amber27 is used to establish upper bounds on the equilibrium dynamics of a glass-forming material at temperatures to 43.6 °C below the conventional Tg—sufficient to discriminate between the VFT function and the upper bounds to the equilibrium dynamics and even among non-diverging models10,11,12,13. The findings that these upper bounds deviate strongly from the ‘classical’ Vogel–Fulcher behaviour challenge classic theories2,3,4,7,8, some modern theories9 and are consistent with the non-diverging models10,11,12,13.
Results
Amber sample
In this work, a 20 million year (Ma) old fossil resin27 from the Dominican Republic (Fig. 1a) was used to study the diverging (or not) dynamics, and the torsion rectangular mode was used to determine the stress relaxation response using a rheometer. Figure 1b shows an amber sample in the testing fixtures.
The advantage of this Miocene amber compared with a normal glass-forming substance is that it has a very long-aging history at ambient conditions. This long-aging history, regardless of the full details, leads to a highly densified material28, which can be used to test the diverging (or not) dynamics described above. Hydrostatic weighing was used here to measure the density difference at room temperature for the 20-Ma-old amber and the same amber after thermal rejuvenation by heating to above Tg followed by cooling to room temperature at 10 K min−1. The 20-Ma-old amber has 2.1% higher density than the latter. Figure 2 shows a schematic of the amber volume or enthalpy beginning with ambient temperature. Importantly, even after 20 Ma, the material has not aged into equilibrium. However, as shown in the figure, as temperature is increased the volume (or enthalpy H) increases and eventually intersects with the equilibrium liquid-state extrapolated parameter. At temperatures below this intersection (H>Heq), the relaxation times measured should be shorter than the equilibrium times owing to the excess of volume or enthalpy relative to the equilibrium state29. Once the equilibrium line is crossed, as temperature increases further, the glass is in a state of lower volume or enthalpy than the equilibrium value (H<Heq). As a result, the relaxation times for these points should be longer than the equilibrium values of relaxation time owing to the high density29—hence they are upper bounds to the equilibrium value.
This shows how extremely dense amber glass provides opportunities to obtain bounds on the equilibirium dynamics below the conventional glass transition temperature by comparing ambe sample with other glasses in a non-equilibrium state and supercooled liquids. τ is the measured relaxation time and τeq is the relaxation time in equilibrium state. After 20 Ma aging, the amber has a very low fictive temperature, as depicted.
DSC results
In order to determine the actual calorimetric state of the amber, we performed differential scanning calorimetry (DSC) measurements. Three thermal loops were performed from −75 °C to 175 °C with the same heating/cooling rate of 10 K min−1. It is well known that the amber resin includes both volatile and non-volatile fractions.30 Most of the volatiles disappear during the aging process and the non-volatile parts (for example, acetogenins, fat and communic acid) become amber by free radical polymerization. Thermal analysis of different ambers, including Dominican amber, reported in the literature31 indicates no mass loss at temperatures well above the maximum temperature of 175 °C examined in the present investigation. The overlap of the second heating scan and the third one indicates that no physical or chemical change occurs in our heating scans to 175 °C (Fig. 3a). Owing to the non-isothermal sub-Tg-aging history (but at temperatures more than 100 °C below the Tg) during millions of years for the amber sample, a broad endothermic shoulder32 is observed in the first heating curve indicative of low-temperature aging and the appearance of sub-Tg peaks that have not yet fully migrated to the vicinity of Tg. This is somewhat different than the sharp peaks seen when aging closer to the glass transition temperature and/or when the sample has aged completely into equilibrium.33,34 Figure 3b shows the first heating curve of the amber sample, and the fictive temperature Tf for the geologically aged amber was found to be 92.6 °C using Moynihan’s method35 such that sum of areas I equals area II (area matching method).
(a) Three heating curves from DSC measurement. (b) First heating curve of amber from DSC measurement showing large enthalpy overshoot and application of Moynihan’s area matching method to obtain the amber fictive temperature Tf. (c) Relative enthalpy versus temperature curve obtained by integrating the first and second heating curves.
The glass transition temperature for the unaged amber on cooling at 10 K min−1 was determined to be 136.2 °C from the second heating curve by calculating the limiting fictive temperature36, also using Moynihan’s method35. By integrating the heat flow curves, we obtained the relative enthalpy versus temperature curves shown in Fig. 3c for both geologically aged and unaged amber. The first heating curve represents the properties of the amber after 20 Ma of aging, and the second one shows the amber after thermal rejuvenation.
Mechanical results
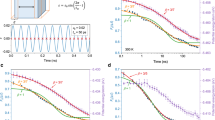
The 20 Ma amber was tested at different temperatures, and at each temperature, Struik’s protocol37 was followed. As a result, we observe an interesting set of behaviours near to the Tf of 92.6 °C and these confirm our hypothesis that we can obtain upper-bound relaxation times for the behaviour between Tg and Tf. In Fig. 4a, we compare the stress relaxation responses after 0.5 and 8 h of aging for the amber at 90 °C. Weak, but normal, physical aging behaviour is observed owing to the excess enthalpy (T<Tf) relative to that of the equilibrium state, that is, the curve at 8 h is shifted to slightly longer relaxation times than is the curve at 0.5 h, hence the material is aging towards a lower enthalpy equilibrium state. At an aging temperature of 95 °C, however, no aging was observed during the 8 h aging (Fig. 4b) indicating that the amber is relatively stable at this temperature. Figure 4c shows the aging responses of the amber at 110 °C and we observe a ‘de-aging’ behaviour. This implies that the amber glass at 110 °C (which is well above the fictive temperature) is evolving towards the higher enthalpy state (see Fig. 2) and the relaxation times measured are longer than the equilibrium values and, therefore, are upper bounds to these values. Figure 4d shows the stress relaxation responses (8 h responses for temperatures below Tg and 0.5 h responses for those above Tg) of amber at the different temperatures investigated. A master (or reduced) curve was obtained from time–temperature superposition6,38 using the curve at 135 °C as the reference. The shift factors so-obtained are the scaled relaxation times  and these are shown in Fig. 5 as a function of temperature.
and these are shown in Fig. 5 as a function of temperature.
(a) Comparison of half-hour and 8-h stress relaxation responses at 90 °C showing normal aging behaviour. (b) Responses during 8 h measurement for amber at 95 °C and the amber is almost stable. (c) Comparison of responses at 110 °C showing shortening of relaxation times during ‘de-aging’ of sample, that is, curves provide an upper bound to equilibrium relaxation response. (d) Master curve obtained by shifting the stress relaxation curves at different temperatures onto the reference curve at 135 °C. Time–temperature superposition was applied here and shift factors (scaled relaxation times) at different temperatures obtained.
(a) Scaled relaxation time versus temperature for all data, from ambient to 160 °C compared with the VFT curve fit to equilibrium data only. Data between Tf and Tg are upper bound to equilibrium response and data for T<Tf are a lower bound to the equilibrium response. (b) VFT plot of scaled relaxation time data for the temperature range from Tf to 160 °C.
It is now of interest to compare the results with the different possibilities of diverging and non-diverging timescales for the dynamics as one reduces the temperature below the Tg and considers the upper bounds to the equilibrium relaxation time. First, the data above Tg (and consequently in equilibrium) was fit to the VFT equation (equation 1). This fit and all of the data are shown in Fig. 5a. The relevant VFT parameters are: B=1071 K and T∞= 338.35 K. We see two things in this figure: below the Tg, the extrapolation of the VFT function deviates greatly from the data—both the upper-bound data and the lower-bound data that are indicated in the plot. We emphasize that while the data within the temperature range between Tf and Tg is not in equilibrium, it provides an upper bound to the equilibrium relaxation time, that is, the equilibrium relaxation time is smaller or equal to our experimental data. Hence, our result actually provides powerful evidence of non-divergence of the dynamics of the amber in this temperature range.
To further examine the problem, we consider two recent models in the literature that suggest that there is no finite temperature divergence of timescales below Tg. We look at the predictions of the Mauro–Yue–Ellison–Gupta–Allan11 model and the parabolic model of Chandler and co-workers12,13. Figure 5b shows a comparison between the models and the experimental data over the range of interest, that is, only the equilibrium data and the upper bound to equilibrium data. As the data are compared on a VFT plot, a straight line would describe the observed behaviour if the material continued on the VFT super-Arrhenius, finite temperature divergent path.
According to the Mauro–Yue–Ellison–Gupta–Allan model11:

Where A, C and K are fitting parameters. Although the Mauro–Yue–Ellison–Gupta–Allan model does not fit the experimental data, it shows better agreement than does the VFT model, that is, it deviates from the VFT extrapolation, though not as much as do the data.
We now turn to the parabolic law model of Chandler and co-workers12,13. In this model, the relaxation times as a function of temperature are written as

where J, T0 and D are fitting parameters. Tx is a crossover temperature (from low T to high T) at which the temperature dependence of relaxation time changes from Arrhenius behaviour to super-Arrhenius response. We fit equation 3 and an Arrhenius function to the experimental data over different temperature ranges and found Tx by comparing the fitting parameters, s.d. and residuals. From our data analysis, we found Tx to be 135 °C, which is close to the glass transition temperature of the thermally rejuvenated amber. The activation energy below Tx is 435.8 kJ mol−1. This apparent activation energy, it does need to be remarked, is that of (essentially) a constant fictive temperature glass and represents the upper-bound relaxation times for this constant fictive temperature glass. The model itself should apply to the equilibrium system. Regardless, within these limitations, we see from the results shown in Fig. 5b that the parabolic law is in good agreement with the data, hence suggesting that Tx itself may be related to the glass transition temperature measured in ordinary experiments. We note that the VFT-determined dynamic fragility39 would be  =90.
=90.
Discussion
We have presented the first measurements of relaxation times on an extremely stable fossil resin (20-Ma-old Miocene amber) to establish upper bounds to the temperature dependence of the dynamics of a glass-forming system far below the conventional glass transition temperature. The 20 Ma age produces an amber with 2.1% higher density than the thermally rejuvenated material and this material was found to have a calorimetric fictive temperature 43.6 °C below the Tg of the thermally rejuvenated material. Hence, the upper-bound relaxation times could be probed this far into the glassy state. We suggest that there may be other ways to probe the sub-Tg equilibrium dynamics (or their bounds) of glass-forming materials than through the use of extremely aged amber. One such possibility may be found in the highly stable glasses of Swallen et al.40 They create the densified glasses by physical vapour deposition and their glasses are as much as 1.7% denser than the thermally rejuvenated glass, hence not as densified as was the 20-Ma-old amber. The Swallen et al.40 group have reported a glass former with the fictive temperature of 31 °C below Tg, versus 43.6 °C in the present work. However, optimization of that procedure could conceivably lead to denser materials. It may also be possible to choose a material with a very low activation energy for the equilibrium relaxation times. For example, Boehm, Ingram and Angell34 reported an Ag7I4AsO4 glass to have an activation energy of 210 kJ mol−1 and a Tg of 63 °C, and which was aged to equilibrium within 1 year at ambient conditions (40 °C below Tg). Even in this case, however, the next 10 °C increment requires several years and achieving equilibrium 60 °C below Tg requires millennia.
Finally, the experimental data for the upper-bound relaxation times of the amber over the range from Tg−43.6 °C to Tg provides a wide enough temperature range to evaluate the validity of different theories and leads to the conclusion that super-Arrhenius behaviour does not exist in the equilibrium state below Tg for amber glass. Whether this is a universal feature of glasses requires further investigation as just suggested. We also find that the parabolic law model, including an activation energy component, from Chandler and co-workers12,13 seems to provide the best description of the data of the models examined and the results suggest that the Tx parameter of the model is related to the conventional glass transition temperature of the thermally rejuvenated glass.
Methods
DSC measurements
A Q20 calorimeter from TA Instruments was chosen to perform the DSC measurements with the same heating/cooling rate of 10 K min−1. The scans were performed in a nitrogen atmosphere. Three thermal loops were performed from −75 °C to 175 °C. The fictive temperature Tf for the geologically aged amber was obtained from the first heat curve using Moynihan’s method35:

where Cpl and Cpg are the liquid and glass heat capacities, respectively. Cp here is the measured value of the as-received amber heat capacity and T* is a temperature much above the transition range. The liquid and glass lines of heat capacity come from the second heating curve.
Mechanical measurements
The amber was cut into a rectangular shape with dimensions of 35.8 × 10.4 × 2.8 mm3 with a band saw blade and sanded to smooth the surface. The dynamics were measured in stress relaxation tests with an ARES rheometer (TA Instruments) over a strain range from 0.03 to 3% depending on the temperature, but always in the linear regime. The geologically aged amber sample was tested from room temperature to 160 °C in a step-wise fashion (10 °C per step at temperature below Tg and 5 °C per step at above Tg) in a N2 atmosphere, and at each step in temperature, short-time stress relaxation experiments were performed following Struik’s protocol37 after aging for successively longer times from 30 min to 8 h. In this way, we monitored the relaxation times of the glass relative to the expected bounds described above.
Struik’s protocol
For the non-equilibrium glassy system, Struik37 developed a protocol to test the physical aging behaviour after a change in temperature, and we follow this protocol in our mechanical testing during our temperature-step experiments. The protocol is shown schematically in Fig. 6. According to Struik’s protocol37, the testing time td is 10% of the aging time te so that the aging process itself will not affect the mechanical response measured, that is, a true representation of the relaxation response is obtained. Also, the aging time sequence is such that, te,i+1=2te,i, that is, a doubling with each subsequent test in order to minimize interactions between successive tests.
Schematic of the Struik protocol.16
Time–temperature superposition
Time-temperature superposition is a reduced time concept which assumes the shape of the viscoelastic response of the material under investigation, here our glass forming system, does not change with temperature.6,38. In other words, all the responses at different temperatures can be shifted to a master curve when one of them is chosen as reference. The horizontal shift factor aT is scaled relaxation time.
Additional information
How to cite this article: Zhao, J. et al. Using 20-million-year-old amber to test the super-Arrhenius behaviour of glass-forming systems. Nat. Commun. 4:1783 doi: 10.1038/ncomms2809 (2013).
References
Anderson, P. W. Through the glass lightly. Science 267, 1615 (1995).
Vogel, H. Das Temperaturabhängigkeitsgesestz der Viskosität von Flüssigkeiten. Phys. Zeit. 22, 645–646 (1921).
Fulcher, G. S. Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 8, 339–355 (1925).
Tammann, G. & Hesse, W. Die abhängigkeit der viskosität von der temperatur bei unterkühlten flüssigkeiten. Z. Anorg. Allg. Chem. 165, 254–257 (1926).
McKenna, G. B. Diverging views on glass transition. Nat. Phys. 4, 673–674 (2008).
Ferry, J. D. Viscoelastic Properties of Polymers 3rd edn Wiley: New York, (1980).
Williams, M. L., Landel, R. F. & Ferry, J. D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 77, 3701–3707 (1955).
Adam, G. & Gibbs, J. On the temperature dependence of cooperative relaxation properties in glass forming liquids. J. Chem. Phys. 43, 139–146 (1965).
Lubchenko, V. & Wolynes, P. G. The shapes of cooperatively rearranging regions in glass-forming liquids. Nat. Phys. 2, 268–274 (2006).
Dyre, J. C., Olse, N. B. & Christensen, T. Local elastic expansion model for viscous-glow activation energies of glass-forming molecular liquids. Phys. Rev. B 53, 2171–2174 (1996).
Mauro, J. C., Yue, Y., Ellison, A. J., Gupta, P. K. & Allan, D. C. Viscosity of glass-forming liquids. Proc. Natl Acad. Sci. 106, 19780–19784 (2009).
Elmatad, Y. S., Chandler, D. & Garrahan, J. P. Corresponding states of structural glass formers. J. Phys. Chem. B 113, 5563–5567 (2009).
Elmatad, Y. S., Chandler, D. & Garrahan, J. P. Corresponding states of structural glass formers. II. J. Phys. Chem. B 114, 17113–17119 (2010).
Xu, B. & McKenna, G. B. Evaluation of the Dyre shoving model using dynamic data near the glass temperature. J. Chem. Phys. 134, 124902 (2011).
O’Connell, P. A. & McKenna, G. B. Arrhenius-type temperature dependence of the segmental relaxation below Tg . J. Chem. Phys. 110, 11054 (1999).
Zhao, J. & McKenna, G. B. Temperature divergence of the dymaics of a poly(vinyl acetate) glass: dielectric vs. mechanical behaviors. J. Chem. Phys. 136, 154901 (2012).
Simon, S. L., Sobieski, J. W. & Plazek, D. J. Volume and enthalpy recovery of polystyrene. Polymer (Guildf) 42, 2555–2567 (2001).
Nozaki, R. & Mashimo, S. Dielectric relaxation measurements of poly(vinyl acetate) in glassy state in the frequency range 10-6-106 Hz. J. Chem. Phys. 87, 2271 (1987).
Badrinarayanan, P. & Simon, S. L. Origin of the divergence of the timescales for volume and enthalpy recovery. Polymer (Guildf) 48, 1464–1470 (2007).
Hecksher, T., Nielsen, A. I., Olsen, N. B. & Dyre, J. C. Little evidence for dynamic divergences in ultraviscous molecular liquids. Nat. Phys. 4, 737–741 (2008).
Shi, X., Mandanici, A. & McKenna, G. B. Shear stress relaxation and physical aging study on simple glass-forming materials. J. Chem. Phys. 123, 174507 (2005).
Hutcheson, S. A. & McKenna, G. B. The measurement of mechanical properties of glycerol, m-toluidine, and sucrose benzoate under consideration of corrected rheometer compliance: an in-depth study and review. J. Chem. Phys. 129, 074502 (2008).
McKenna, G. B. Long-Term Durability of Polymeric Matrix Composites Chapter 7, Springer: New York, ((2012).
Kauzmann, W. The nature of the glassy state and the behavior of liquids at low temperatures. Chem. Rev. 43, 219–256 (1948).
Gibbs, J. H. & DiMarzio, E. A. Nature of the glass transition and the glassy state. J. Chem. Phys. 28, 373 (1958).
Huang, D., Simon, S. L. & McKenna, G. B. Equilibrium heat capacity of the glass-forming poly(α-methyl styrene) far below the kauzmann temperature: the case of the missing glass transition. J. Chem. Phys. 119, 3590 (2003).
Iturralde-Vinent, M. A. & MacPhee, R. D. E. Age and paleogeographical origin of Dominican amber. Science 273, 1850–1852 (1996).
Kovacs, A. J. Glass transition in amorphous polymers. A Phenomenological Study. Fortschr. Hochpolym.-Forch 3, 394–507 (1963).
Doolittle, A. K. Studies in Newtonian flow. I. the dependence of the viscosity of liquids on temperature. J. Appl. Phys. 22, 1031–1035 (1951).
Langenheim, J. H. Amber, Resinite, and Fossil Resins Chapter 1 ( American Chemical Society: Washington, DC, (1995).
Ragazzi, E., Roghi, G., Giaretta, A. & Gianolla, P. Classification of amber based on thermal analysis. Thermochim. Acta 404, 43–54 (2003).
Hodge, I. M. & Berens, A. R. Calculation of the effects of annealing on sub-Tg endotherms. Macromolecules 14, 1598–1599 (1981).
Echeverria, I., Su, P. C., Simon, S. L. & Plazek, D. J. Physical aging of a polyetherimide: creep and DSC measurements. J. Polym. Sci. B Polym. Phys. 33, 2457–2468 (1995).
Boehm, L., Ingram, M. D. & Angell, C. A. Test of a year-annealed glass for the cohen-grest percolation transition. J. Non-Cryst. Solids 44, 305–313 (1981).
Moynihan, C. T., Easteal, A. J. & Deboil, M. A. Dependence of the fictive temperature of glass on cooling rate. J. Am. Ceram. Soc. 59, 12–16 (1976).
Badrinarayanan, P., Zheng, W., Li, Q. & Simon, S. L. The glass transition temperature versus the fictive temperature. J. Non-Cryst. Solids 353, 2603–2612 (2007).
Struik, L. C. E. Physical Aging in Amorphous Polymers and Other Materials Elsevier: Amsterdam, (1976).
O’Connell, P. A. & McKenna, G. B. Large deformation response of polycarbonate: time-temperature, time-aging time, and time-strain superposition. Polym. Eng. Sci. 37, 1485–1495 (1997).
Qin, Q. & McKenna, G. B. Correlation between dynamic fragility and glass transition temperature for different classes of glass forming liquids. J. Non-Cryst. Solids 352, 2977–2985 (2006).
Swallen, S. F. et al. Organic glasses with exceptional thermodynamic and kinetic stability. Science 315, 353–356 (2007).
Acknowledgements
We thank the National Science Foundation under awards DMR-0804438 and DMR-1207070 (to J.Z. and G.B.M.), and the John R. Bradford endowment at Texas Tech University (to J.Z. and G.B.M.), each for partial support of this work. We also thank Y. Li for help with the curve fitting to the glass models. We also thank Y. Goldman of The Dead Bug in Amber Club for the provision of the amber.
Author information
Authors and Affiliations
Contributions
The original ideas for this project were from G.B.M. J.Z. performed the experiments and wrote the manuscript under the supervision of G.B.M. S.L.S. contributed through the data analysis of the calorimetric measurements. The data analysis of the physical aging was performed by J.Z. under the supervision of G.B.M. All three authors also contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Zhao, J., Simon, S. & McKenna, G. Using 20-million-year-old amber to test the super-Arrhenius behaviour of glass-forming systems. Nat Commun 4, 1783 (2013). https://doi.org/10.1038/ncomms2809
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2809
This article is cited by
-
Correlating dynamic relaxation and viscoelasticity in metallic glasses
Science China Physics, Mechanics & Astronomy (2024)
-
Challenging the Kauzmann paradox using an ultra-stable perfluoropolymer glass with a fictive temperature below the dynamic VFT temperature
Scientific Reports (2023)
-
Emergence of equilibrated liquid regions within the glass
Nature Physics (2023)
-
Ultrastable glasses: new perspectives for an old problem
La Rivista del Nuovo Cimento (2022)
-
Hierarchical aging pathways and signatures of thermodynamic transition in molecular glasses
Science China Materials (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.