Introduction

Owing to structural, charge, orbital or spin reconstruction at their interfaces, complex oxide heterostructures have emerged as an avenue for creation of exotic phenomena that are absent in their bulk constituents1. One of the most exciting systems of such heterostructures is the interface between two band insulators LaAlO3 and SrTiO3. When these two perovskite type oxides are brought together along the (100) orientation, a highly conducting two-dimensional electron gas (2DEG) emerges at their interface2. Further, this interface has also been shown to exhibit various electronic and magnetic phases such as a tunable metal-insulator ground state3, two-dimensional superconductivity4,5, magnetic ground state6 and an electronic phase separation7 in which different magnetic phases are present together with the interface conductivity. Most recently, the coexistence of mutually exclusive phenomena, magnetism and superconductivity is also reported8,9,10. Nevertheless, all of these studies were specific only to the interfaces constructed along the (100) crystallographic orientation.

The conductivity in crystalline LaAlO3/SrTiO3 (100) interface is mostly interpreted to originate from electronic reconstruction, which is a direct consequence of the polarization discontinuity11 at the interface between the two oxides. In this case, the ABO3 perovskite structure of the SrTiO3 (100) substrate can be considered as stacks of (SrO)0 and (TiO2)0 (Fig. 1a), whereas for the LaAlO3, it consists of charged sheets of (LaO)+1 and (AlO2)−1, which leads to a polarization discontinuity at the interface between the LaAlO3 and SrTiO3. On the other hand, for the case of LaAlO3/SrTiO3 interfaces prepared on SrTiO3 (110) substrate (Fig. 1c), both the SrTiO3 and LaAlO3 can be represented by planar stacks of (ABO)+4 and (O2)−4 layers as proposed in Hwang et al.12 and Mukunoki et al.13 which leads to no polarization discontinuity at the interface. Consequently, no conductivity would be expected for such LaAlO3/SrTiO3 (110) interfaces.

Figure 1: Interface configurations.
figure 1

Layout of the polar catastrophe model for LaAlO3/SrTiO3 interface on (a) (100)- and (c) (110)-oriented SrTiO3 substrates, where planes are segmented as planar charge sheets. In the case of (100), charge transfer is expected, whereas in the case of (110), there is no polarization discontinuity and hence no charge transfer. (b,d) Atomic picture of the interfaces for representations (a) and (c), respectively. (e) Atomic picture of LaAlO3/SrTiO3 interface on (110)-oriented SrTiO3, considering the (110) planes of SrTiO3 and LaAlO3 as buckled sheets.

Full size image

Here we demonstrate that a high-mobility 2DEG can also arise at this LaAlO3/SrTiO3 (110) interface. The (110) interface shows transport property and LaAlO3-layer critical thickness for the metal-to-insulator transition similar to those of (100) interfaces, but with a strong anisotropic characteristic along the two in-plane crystallographic directions. This anisotropic behaviour is further found to be sensitive to the oxygen growth condition. The density functional theory (DFT) study shows that the energetically favourable atomic structure along the (110) orientation can support the electronic reconstruction when the interface is represented by an alternate way in which the polarization discontinuity is still present.

Results

Electrical transport properties

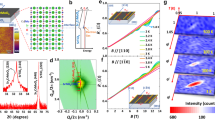
The growth parameters for the LaAlO3/SrTiO3 (110) and (100) samples are discussed in the Methods section. The sheet resistance, Rs, charge density, ns, and Hall mobility, μ, were measured using a van der Pauw geometry. Figure 2a shows Rs versus temperature for the LaAlO3/SrTiO3 (110) samples grown at different oxygen partial pressures () with a fixed thickness of 12 unit-cells (uc) LaAlO3. Strikingly, these interfaces show conductivity reminiscent to the (100) case (Fig. 2b), albeit with a larger dispersion with respect to the oxygen pressure during growth. The Rs follows a T2-like dependence over a temperature range of 300–100 K and tends to saturate at low temperatures. The samples grown at higher oxygen pressures show a resistance upturn at lower temperatures, a typical localization/Kondo behaviour indicating the presence of magnetic scattering centres at the interface. Although Kondo scattering in the (100) case is reported only for LaAlO3 thickness >15 uc (refs 6,14,15), in the case of (110), it is seen even for 10 uc LaAlO3 thickness, indicating stronger scattering effects. We note here that for the (100) case, the dispersion in the resistivity with oxygen deposition pressures was also reported but for samples with ‘thicker’ LaAlO3 layers of 20 uc (ref. 6), implying different sensitivity to the LaAlO3 thickness between these interfaces. Interestingly, there is a temperature shift in the resistance-minimum with the oxygen growth pressure, indicating that the strength of the scattering at the interface is sensitive to the deposition conditions. We note here that resistivity measurements have been carried out down to 2 K, and it is feasible that some of these samples may become superconducting at lower temperatures.

Figure 2: Transport properties.
figure 2

Temperature dependence of the sheet resistance Rs (T) of the LaAlO3/SrTiO3 interfaces for different oxygen partial pressures () during growth on (a) (110)- and (b) (100)-oriented SrTiO3 substrates. Temperature dependence of carrier density ns(T) and Hall mobility μ(T) of the LaAlO3/SrTiO3 interfaces for different during growth on (c) (110)- and (d) (100)-oriented SrTiO3 substrates.

Full size image

Figure 2c shows the corresponding variation in ns and μ with temperature for the LaAlO3/SrTiO3 (110) and (100) samples grown at different . For the (110) samples, ns decreases with decreasing temperature, and for the samples grown at higher partial pressures, ns at low temperature (2 K) tends towards a constant value of about 1.5 × 1013 cm−2, which is somewhat lower than the residual carrier density of about 2.5 × 1013cm−2 for the LaAlO3/SrTiO3 (100) samples. This could be due to the preferred occupancy of the Ti-3d orbitals at the interface, which may localize some of the electrons16,17. For the thermally activated charge carriers in the (110) samples, we find an activation energy of about 9 meV, whereas in LaAlO3/SrTiO3 (100) interfaces, an activation energy of 6.0 meV has been reported18,19. For both orientations, the measured μ follows a power law temperature dependence for T>100 K, as μ~5 × 106 T−2.2. All the samples grown at higher pressures show μ values of the order of 200–600 and 2–7 cm2 V−1 s−1 at 2 and 300 K, respectively. These values correspond well with those reported in literature for the LaAlO3/SrTiO3 (100) interfaces3,14,20. We notice a decrease in the μ in the (110) case, simultaneous with Kondo features becoming visible in the Rs(T) curves. For the (110) sample grown at 5 × 10−5 Torr, the ns at 300 K is 4.9 × 1014 cm−2, which has the μ of 12,000 cm2 V−1 s−1 at 2 K, suggesting contribution from other sources such as oxygen vacancies20,21 and defect centres present near the interface.

Thickness-dependent insulator to metal transition

One of the characteristic features of the LaAlO3/SrTiO3 (100) interfaces, and considered as one of the most important arguments for a polarization discontinuity driven mechanism, is the dependence of the sheet conductivity on the number of ucs of LaAlO3 with the observation of an insulator to metal transition at 3–4 uc of LaAlO3 layers3. In Fig. 3, the conductivity versus the number of LaAlO3 ucs N grown on the SrTiO3 (110) substrates is plotted. Here also we clearly see two regimes, an insulating one at low N (N<3) and a metallic state at higher N (N≥4) values.

Figure 3: LaAlO3 thickness dependence of sheet conductivity.
figure 3

The room-temperature sheet conductivity as a function of number of ucs of LaAlO3 for the LaAlO3/SrTiO3 (110) samples, clearly showing the insulator to metal transition (data points marked with open red circle are for a sample initially having 3 uc of LaAlO3, followed by the growth of two more uc making it 5 uc in total).

Full size image

Considering all the data presented above, it is remarkable that the (110) samples are not only conducting but also bear remarkable similarities to the conductance properties of the (100) case. However, there are also strong differences, the most noticeable of which is the anisotropy of the conductance.

Anisotropy of electronic transport

Figure 4a show the electrical transport characteristics of the LaAlO3/SrTiO3 (110) samples along the [10] and [001] directions, respectively, demonstrating the anisotropic transport behaviour as a function of along the two crystallographic directions. Strikingly, along [10] direction, strong localization effects are seen at low temperatures, whereas along [001] direction, such localizations are absent. A basic difference between these two directions is the presence of linear Ti-O-Ti chains along [001] and buckled Ti-O-Ti chains along [10] as depicted schematically in Fig. 4c. The deposition pressure dependence of Rs at 2 K is plotted in Fig. 4d for both directions. Clearly, the conductivity along the [10] direction has a much stronger dependence on deposition pressures compared with the [001] direction, indicating the strong role of the differences in the Ti-O-Ti chain along the two orthogonal directions. The anisotropy arising from other effects such as step edges22 has been measured for (100) case (Supplementary Fig. S1), and this is substantially smaller than what we see in the (110) case and so we can rule out step edge scattering as the dominant mechanism.

Figure 4: Anisotropic conductivity of theLaAlO3/SrTiO3 (110) interfaces.
figure 4

Rs(T) measured along (a) [10] and (b) [001] directions for the LaAlO3/SrTiO3 (110) samples grown at different oxygen partial pressures. (c) Schematic view of the Ti chain arrangement along the [10] and [001] directions. (d) Deposition oxygen pressure dependence of Rs at 2 K measured along the [10] and [001] directions.

Full size image

Origin of conductivity and interface structure

The fact that there are many similar properties to the (100) case, even including the insulator to metal transition at around 4 uc of LaAlO3, indicates that a very similar mechanism is at work for the formation of the 2DEGs for both (100) and (110) cases. Recently, Stengel et al.23 discussed the issue of polarity in various oxides, especially the case of LaAlO3 and SrTiO3 surfaces, where it is shown that in LaAlO3 case, the surface with cleavage planes are shown to be energetically favourable than a simple polar (001) surface. In analogous to this, our DFT calculation results suggest that buckled TiO termination at SrTiO3 (110) surface is more favourable than a hypothetical polar stoichiometric SrTiO surface (Supplementary Fig. S2). In this scenario, the atomic structure of the interface would be critical23 to determine polarity effects at these heterostructures. We further perform DFT calculations on the LaAlO3/SrTiO3 (110) interface and found that the origin for the unexpected conductivity in the (110) case can also be explained by considering energetically stable buckled TiO termination, resulting in a modified polarization discontinuity with an interface viewed as depicted in Fig. 1e (buckled interface) rather than the one in Fig. 1c (planar interface).

The electronic configuration of interfaces with such a buckled interface structure as in Fig. 1e was modelled by DFT as shown in Fig. 5a. Indeed as shown in Fig. 5b, an insulator to metal transition with increasing number of LaAlO3 monolayers is obtained. The critical thickness for insulator to metal transition is about 4 uc, which is in agreement with our experimental observation. This result shows that by viewing the LaO/TiO2 as buckled layers, the thickness dependence of the insulator to metal transition arising from avoiding the polarization catastrophe can be reproduced24. Figure 5c shows the partial density of states for O-2p projected onto each layer. From the figure, we can see clearly that the top of the valence band moves towards Fermi level as we approach the surface, suggesting that there can still exists an intrinsic electrostatic fields to avoid the polar catastrophe due to the polar discontinuity caused by the buckled interface. This intrinsic electrostatic field can induce the insulator to metal transition when this electrostatic potential exceeds the band gap. In our case, this transition occurs at N<4 as shown in Fig. 3. Note, however, the critical value of N might depend on approximations used for calculations; we also find by performing generalized gradient approximation (GGA)+U calculations that the main conclusion are qualitatively the same. Thus, the DFT study reveals that the interface between LaAlO3 and the energetically favourable atomic structure of the TiO-terminated SrTiO3 (110) can support the conductivity with the interface that is represented by an alternate way, namely, the buckled interface shown in Fig. 1e, in which the polarization discontinuity is still present.

Figure 5: DFT calculations.
figure 5

(a) Schematic cell structure of LaAlO3/SrTiO3 (110) interface with TiO-terminated SrTiO3 (110) for six monolayers of LaAlO3. (b) The total density of states for different numbers N of LaAlO3 monolayers deposited on SrTiO3 (110) clearly shows the band gap decrease with increasing N and an insulator to metal transition occurring at 4 uc. (c) The partial density of states for O-2p projected onto each layer for N=6 monolayers of LaAlO3 deposited onto TiO-terminated (110) SrTiO3. Here the top of valance band for each monolayer is indicated by dashed lines. The Fermi level is denoted by EFermi. Here IF represents interface.

Full size image

To investigate the possibility of such proposed buckled atomic structure at the (110) interfaces, we performed cross-sectional scanning transmission electron microscopy (STEM) on the LaAlO3/SrTiO3 (110) interfaces. Figure 6 shows a high-angle annular dark-field STEM image of the LaAlO3 film grown on the SrTiO3 (110) substrate. The image shows a perfect epitaxial growth of the LaAlO3 across the interface of the heterostructure along the (110) orientation. The signal from the atom columns depends on the atomic number25. The ratio between the signals of the Al and La atom columns is expected to be <10%. In addition, the projection along the Al atom columns also includes O atoms further adding to the background signal of the Al columns. We also note that the background intensity is generally higher in LaAlO3 compared with the result of (100) interfaces26. The Al and Ti (B-site) atom columns are visible in the STEM images. However, it is found that it is difficult to use them as indicators of the interface between the LaAlO3 and SrTiO3 film on the basis of poor signal to background ratio. Therefore, the La and Sr (A-site) atom columns have been used as indicators for the film/substrate interface. In Fig. 6, a higher resolution of elemental mapping at the interface representing the arrangement of La (red) and Sr (blue) positions in both LaAlO3 and SrTiO3 is also shown. We notice some of the La and Sr atoms at the interface extend up to 2–4 uc rather than 2 uc as anticipated. Both the sparseness of such extended facets and the absence of connectivity among them rule out other mechanisms for conduction (for example, an effective (100) interface at 45 degrees). However, the models in Fig. 1d cannot be distinguished just by identifying only the A-site cations as in our current STEM data. Therefore, one needs to further resolve the chemical identity of the B-site cations alongside A-site cations to confirm the proposed buckled structure in Fig. 1e.

Figure 6: Transmission electron microscopy.
figure 6

High-angle annular dark-field STEM images of the LaAlO3 film on the SrTiO3 (110) substrate shows an epitaxial growth of the LaAlO3/SrTiO3 (110) heterostructure (A-site atoms La and Sr are indicated by red and blue, respectively, and the B-site atoms Al and Ti by orange and purple, respectively). A magnified view of the elemental mapping across the interface is also shown on the right side. Scale bar, 2 nm.

Full size image

Discussion

The importance of the (110) interface is better brought out in context with what has been learnt so far with the (100) interfaces. The 2DEG at the LaAlO3/SrTiO3 (100) interfaces has been studied under a variety of deposition conditions, layer thicknesses and externally applied fields27,28. In most of these experiments, the 2DEG was presumed to be the result of a direct manipulation of electrostatic potential at the interface to promote electrons to the conduction band of SrTiO3, which requires energy of the order of 3.2 eV. However, recently the 2DEG was also demonstrated on the surface of SrTiO3 by shining ultraviolet light29, vacuum cleaving30 and chemical reduction of the surface during growth31. It is apparent that the 2DEG can be produced by different mechanisms, which can elevate the electron to the conduction band of SrTiO3. Recent experimental work involving amorphous over layers on SrTiO3 showing a conducting interface has brought in the importance of interface chemistry31. Under this scenario, oxygen diffusion from SrTiO3 surface during film growth into the over layers was deemed responsible for the interface conductivity. What was striking was the similarity of the results between the amorphous and crystalline over layers in terms of the saturation in charge density and conductivity with the film thickness. Unlike their crystalline counterparts, however, one of the short comings of the amorphous over layers seems to be the thermal stability of the interfaces that lose their conductivity subsequent to a 150 °C anneal in air, which will make them unsuitable for device applications (crystalline samples in our case were found to be stable post annealing and preserve conductivity). The real attraction of the crystalline interfaces is that they offer a variety of controllable parameters such as strain32, correlation effects33 through structure coupling and large anisotropy (as shown here), which can be used to manipulate the interface properties.

Our experiments and DFT calculations using (110) substrates show that the polarization catastrophe model may still be valid for crystalline LaAlO3/SrTiO3 interfaces, provided the interface is viewed appropriately (buckled interface). Because of the different atomic structure in the (110) interfaces, the presence of buckled Ti-O-Ti chains opens up new possibilities, which may lead to new phenomena. For example, the anisotropy can be further explored by nano-structuring the 2DEG along the anisotropic crystallographic axis with techniques such as charge writing using atomic force microscopy34, which is already shown to create new properties. The other effect of the crystallographic anisotropy is on the reported spin-orbit interaction35, which would further attract a lot of interest to explore the electric field effects on these anisotropic surfaces. Further investigation of the anisotropy on other phenomena (magnetism and superconductivity) will be of interest for the community and may lead to new physics and device applications.

Methods

Substrate treatment

For the (100) case, substrates were treated with well-established conditions; buffered HF for 30 s followed by thermal annealing at 950 °C for 2 h in air36,37. For the (110)-oriented SrTiO3, the substrates were annealed for 3 h at 1050 °C in air38. The step height in this case is about 0.28 nm, which is the uc spacing along the [110] direction. The step edges appear to be facetted along the [001] and [10] low-index crystallographic directions, giving rise to the triangular-shaped steps39 (Supplementary Fig. S3). Reflection high-energy electron diffraction analysis on the SrTiO3 (110) surface shows a signature of a (1 × 3) reconstructed surface (Supplementary Fig. S4).

Sample growth

The LaAlO3/SrTiO3 (110) samples were prepared with various LaAlO3 thicknesses (N) from 1 to 14 uc under different ranging from 5 × 10−5 to 5 × 10−3 Torr on atomically smooth SrTiO3 (110) substrates. The LaAlO3 films were deposited from a single-crystal LaAlO3 target at 720 °C by pulsed laser deposition. The laser (248 nm) energy density was 1.4 J cm−2 and repetition rate was 1 Hz. During deposition, the film growth was monitored using in-situ reflection high-energy electron diffraction. After deposition, all samples were cooled to room temperature at 10 °C min−1 in oxygen at the deposition pressure. For comparison, LaAlO3/SrTiO3 (100) samples were grown with 12 uc LaAlO3 layers under the same preparation conditions.

Structural analysis

Thicker LaAlO3 films of about 15 nm were grown to enable confirmation of the growth orientation of the LaAlO3 on SrTiO3 (110) and (100) substrates by X-ray diffraction (Supplementary Fig. S5). Samples for STEM were prepared by using cutting, mechanical grinding, polishing and low-voltage Ar-ion beam milling as a final polishing step. High-angle annular dark-field STEM images were recorded using a FEI Titan 80–300 microscope with a corrector for spherical aberration of the condenser lenses and a monochromator. The microscope was operated at 300 kV. The electron beam is incident along the [001] direction to the LaAlO3/SrTiO3 (110) interface.

Electrical characterization

Electrical characteristics for all the samples were measured with the van der Pauw technique. Ohmic contacts onto four corners of a 5 × 5 mm2 sample were formed using Al wedge bonding directly connected to the sample interface. Sheet carrier density ns and carrier mobility μ were determined as ns=1/eRH and μ=RH/Rs, where Rs is the sheet resistance and RH is Hall coefficient. For the directional-dependence transport measurements, crystallographic directions on the surface of substrate were identified as specified by the substrate supplier (Crystec GmbH).

Density functional theory

First-principles calculations based on the DFT for LaAlO3/SrTiO3 (110) interface was performed. We used the GGA (ref. 40) and the projected augmented wave method with a plane wave basis set as implemented in the Vienna Ab initio Simulation Package41,42,43. To study the thickness dependence of LaAlO3 monolayers deposited on SrTiO3 (110) substrate, we use a slab model shown in Fig. 5a. Here, as usual, the inversion symmetry of the slab is assumed to avoid spurious electronic field. In all calculations, a vacuum region of 12 Å between repeated slabs is taken. A kinetic energy cut off is set to be 400 eV for the plane wave basis and the slab is sampled with 8 × 8 × 1 k-point grid in combination with the tetrahedron method. Although the in-plane lattice constant is fixed at the relaxed lattice constant of bulk SrTiO3 (a=3.944 Å), all coordinates of atomic positions along the c-direction perpendicular to the interface are fully relaxed until the forces become <0.01 eV Å−1. We have carefully checked the convergence of our calculations. Our calculations show that the energy gap for bulk SrTiO3 is about 1.8 eV, separating the valence band with O-2p characters and the conduction band mainly composed of Ti-3d. For LaAlO3, we obtain the band gap of 3.2 eV. These estimated values of the band gap are similar to the ones previously reported by DFT calculations34 and are smaller than the ones observed experimentally. However, the underestimation of the energy gap within GGA is well known, and the GGA+U approach, for instance, gives an improved description.

Additional information

How to cite this article: Annadi, A. et al. Anisotropic two-dimensional electron gas at the LaAlO3/SrTiO3 (110) interface. Nat. Commun. 4:1838 doi: 10.1038/ncomms2804 (2013).