Abstract
The revolutionary rise of broad-leaved (flowering) angiosperm plant species during the Cretaceous initiated a global ecological transformation towards modern biodiversity. Still, the mechanisms involved in this angiosperm radiation remain enigmatic. Here we show that the period of rapid angiosperm evolution initiated after the leaf interior (post venous) transport path length for water was reduced beyond the leaf interior transport path length for CO2 at a critical leaf vein density of 2.5–5 mm mm−2. Data and our modelling approaches indicate that surpassing this critical vein density was a pivotal moment in leaf evolution that enabled evolving angiosperms to profit from developing leaves with more and smaller stomata in terms of higher carbon returns from equal water loss. Surpassing the critical vein density may therefore have facilitated evolving angiosperms to develop leaves with higher gas exchange capacities required to adapt to the Cretaceous CO2 decline and outcompete previously dominant coniferous species in the upper canopy.
Similar content being viewed by others
Introduction
Almost 90% of present-day terrestrial plant biodiversity consists of flowering (angiosperm) species1. This ecological success of angiosperms did not grow gradually, rather, angiosperms so suddenly dominated the fossil record of the Cretaceous period between 145 and 66 million years (Ma) ago that even Charles Darwin found it challenging to his ideas on gradual evolution2,3. Evidence is now emerging that ancestral angiosperms existed in low evaporative niches during the Early Cretaceous4,5 before the period of their rapid diversification in the Mid Cretaceous6. During the Late Cretaceous, evolving angiosperms spread poleward7 and gained ecological dominance in most of the world’s ecosystems by replacing needle-leaved (gymnosperm) conifer tree species in the evaporatively more demanding upper canopy8 (Fig. 1a). Previous explanations for this angiosperm radiation1 include coevolution with insects9 and positive environmental feedbacks10. Recent insights11 suggest that the evolution towards more reticulated leaf venation12,13 was linked to the escalation of angiosperm leaf gas exchange capacity14,15 in relation to falling atmospheric CO2 concentrations (Ca)16,17 during this floral regime shift. The resulting rise in productivity likely enabled evolving angiosperms to outcompete conifers in the upper canopy18. However, the underlying mechanisms involved in this angiosperm revolution remain unrevealed.
(a) The angiosperm radiation occurred at the expense of pteridophytes (horsetails, ferns) and cycadophytes (cycades) living near the forest floor and conifers dominating the upper canopy1,6,7,8. (b) Modelled Ca from the GEOCARBSULF model51 with parameterisations for standard (GEOsw), moderate (GEOmw) and enhanced (GEOew) volcanic weathering rates, following Fletcher et al.17 (c) Falling Ca likely drove leaf evolution towards higher stomatal gas exchange capacity via decreasing pore size and rising stomatal density (Ds)19,24. Data points indicate observations of fossil Ds24, the black line indicates the upper bound on modelled stomatal conductance to water vapour (gsw)19. (d) Rising angiosperm leaf vein density (Dv) obtained from fossil leaves15 and age-calibrated ancestral-state analyses14. The dashed sigmoid curve is based on the equation: Dv=3.3+5.3/(1+e−(time −130)/−8.7) following Brodribb et al.14 In this equation the parameter ‘time’ is time in million years BP. Also indicated are ranges of modern angiosperm Dv for woody shade demanders, canopy trees and for trees in megathermal rain forests, following Feild et al.15 (e) Schematised cross-sections of a conifer needle leaf (top), an early hypostomatous angiosperm broad leaf (middle) with low Dv and low Ds, and a modern hypostomatous angiosperm broad leaf (bottom) with high Dv and high Ds.
Falling atmospheric CO2 concentrations (Ca) before and during the angiosperm radiation16,17 (Fig. 1b) likely put evolutionary pressure on terrestrial C3 plants19 because carbon uptake for photosynthesis is intrinsically linked to transpirative water loss through the stomatal pores on their leaf surfaces20. Natural selection may therefore have favoured those species with most plastic stomatal traits21,22 capable of optimizing photosynthesis with minimal transpiration19,23. Consequentially, falling Ca drove leaf evolution towards higher maximal stomatal conductance (gsmax)24 (Fig. 1c). The exchange of water vapour for CO2 through stomata is principally determined by diffusion according to Fick's law and Stefan's law25,26, which are combined in the general expression for gsmax given by equation (1)27 (see Methods section). In this equation, Fick’s law relates the rate of steady-state diffusion to the concentration gradient across the stomatal pore, whereas Stefan's law describes the familiar ‘end correction’ component of the pore resistance27. As smaller stomata reduce the diffusion distance across the stomatal pore and limit the resistance of the ‘end correction’ term in equation (1), evolution towards higher gsmax was necessarily linked to a reduction in stomatal size combined with an increase in stomatal density24 (Fig. 1c). Coeval with this rise in gsmax, the geologic record reveals a two-phased rise in angiosperm leaf vein density (Dv)14,15 during the Cretaceous (Fig. 1d). The first phase in rising angiosperm Dv occurred around 100 Ma during the Late Albian15 when, for the first time, the non-angiosperm maximum Dv of ~6 mm mm−1 was surpassed. The second phase occurred in the latest Cretaceous and earliest Tertiary (around 60 Ma), during which the first modern values of angiosperm Dv in excess of ~10 mm mm−2 are observed and angiosperm leaf gas exchange capacity escalated15. As a reference to the Cretaceous rise in angiosperm leaf venation, modern values of Dv observed in woody shade demanders, in canopy trees and in extant megathermal rain forests are also indicated in Fig. 1d15. Although the evolution towards more reticulated leaf venation appears to have occurred on the backdrop of the Cretaceous Ca decline (cf. Fig. 1), relating rising angiosperm leaf venation to falling Ca remains elusive28. Plant physiological modelling does suggest that the combined effect of higher Dv and higher gsmax may have enabled evolving angiosperms to increase leaf gas exchange rates to offset the adverse effects of falling Ca for productivity14,19. However, to benefit from such highly conductive leaves in terms of additional growth and reproduction, the required additional carbon investments in water transport tissue should have been paid off by a larger increase in carbon gain11,12,13.
On the basis of a combination of data and modelling approaches, we propose and substantiate a novel mechanism to explain why evolving angiosperms could suddenly expand their leaf gas exchange capacity during the Cretaceous, and why conifers could not. This proposed mechanism is based on the consequences of morphological differences between planar-shaped hypostomatous (angiosperm) broad leaves and tubular shaped (conifer) needle leaves for the leaf interior transport paths of CO2 and water (Fig. 1e). We note that also non-angiosperm species evolved planar-shaped leaves with a variety venation structures29; however, these morphologies did not evolve the high Dv values common to modern upper canopy angiosperm species14,15,20. In our schematization of the broad-leaf morphology we differentiated between the Early Cretaceous angiosperm morphology with low Dv and low Ds and the modern angiosperm morphology with high Dv and high Ds. Common for all leaf morphologies is that CO2 moves from the leaf boundary layer, through the stomatal pore and substomatal cavity into the intercellular airspaces30. From there, CO2 is absorbed in the mesophyll cells where photosynthesis occurs in the chloroplasts31. Water moves from the soil through the plant’s water transport system up to the leaf veins before it evaporates and passes through the stomata. The exact mechanisms responsible for leaf interior water transport beyond the vein endings up to the stomata remain debated32, but may involve a liquid-phase flow through the apoplast, across individual cells and through plasmodesmata with evaporation occurring close to the stomata in the substomatal cavitiy. Alternatively, evaporation may occur deeper inside the leaf throughout the mesophyll33 or close to the leaf vein endings34,35, with water being transported as a vapour across the intercellular airspaces up to the stomata. Recent advances highlight the importance of this vapour-phase water transport mechanism in regulating short-term stomatal responses36,37. Currently, neither the liquid-phase mechanism nor the vapour-phase mechanism can unambiguously be falsified32. Moreover, both water transport mechanisms may occur in parallel or involve a mixed phase38. We therefore explored the role of both mechanisms in relation to the sudden ecological success of angiosperms during the Cretaceous. We find that the period of rapid angiosperm evolution initiated after the leaf interior (post venous) transport path length for water became shorter than the leaf interior transport path length for CO2. This transition may have enabled the evolving angiosperms to develop leaves with higher gas exchange capacities required to adapt to the Cretaceous CO2 decline and outcompete previously dominant coniferous species in the upper canopy.
Results
Postvenous liquid water transport and photosynthesis
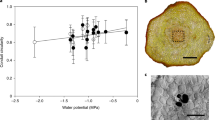
Considering the postvenous liquid-phase water transport mechanism, the maximum gas exchange capacity of a leaf is crucially constrained by its hydraulic conductance (Kleaf) and the maximal leaf water potential gradient (Δψleaf) before tissue damage and hydraulic failure occurs20. A key determinant in Kleaf is the maximum path length for postvenous water transport (). As shown in Fig. 2a, a log-linear relation exists between and Kleaf across species20. An important consequence of the evolutionary rise in angiosperm Dv was therefore the reduction in by bringing the leaf vein endings closer to the stomatal pores (Fig. 2b). The physiological advantage of the high Dv in modern angiosperms is likely to be related to facilitating leaf water transport within the range of permissible Δψleaf (ref. 20) before stomata close to protect plants from hydraulic failure39. The rise in Dv may therefore have provided evolving angiosperms with a means to offset a rising transpirational demand associated with higher stomatal conductance and the functioning in environments with lower atmospheric humidity, such as the upper canopy. The relation between Dv and stomatal conductance under variable atmospheric humidity is illustrated in Fig. 2c using a semi-empirical model14. This model assumes steady-state equilibrium between the liquid flux of water through the leaf interior up to the substomatal cavity, and the transpiration flux of water vapour through the stomata. The potential maximum photosynthetic carbon return from this water flux was calculated with the biochemical demand model of Farquhar et al.40 This calculation involved the assumption that stomatal conductance to water vapour (gsw) equals stomatal conductance to CO2 (gsc) when compensated for the difference in diffusivity between water vapour and CO2 (that is, gsw=α·gsc, with α=1.6). Although leaf venation is not the only determinant in linking leaf water transport to photosynthesis14,20, the modelled values of gsw (Fig. 2c) imply that rising Dv may have enabled evolving angiosperms to sustain photosynthesis under increasingly low atmospheric humidity and under falling Ca (Fig. 2d). These results indicate that the sudden rise in angiosperm Dv that occurred during the Cretaceous was related to their coeval radiation from the forest floor towards the upper canopy4. However, as shown previously by Boyce and Zwieniecki28 using the same semiempirical model based on the liquid-phase mechanism14, there appears to be little carbon uptake advantage from increasing Dv beyond ~8 mm mm−2. Other mechanisms are therefore required to explain why angiosperm leaf venation evolved so suddenly beyond 6–10 mm mm−2 during the Late Cretaceous.
(a) Log-linear relation between and the leaf hydraulic conductance (Kleaf) across species. Data are derived from Brodribb et al.20 and includes observations on angiosperms, gymnosperms, byrophytes, ferns and lycophytes. Gymnosperm species with accessory transfusion tissue were omitted. A highly significant quadratic regression describing these data is: Kleaf=0.259 +1.41 +0.60 (r2=0.94, P<0.001). (b) Geometric relation between Dv and . Calculations show differences in vein-epidermis distance (dyw) covering a typical range of 70–130 μm (refs 5,14,20). (c) Calculations with a semiempirical model14 that relates Kleaf to the stomatal conductance to water vapour (gsw) under steady-state transpiration with variable Dv. The role of rising Dv in allowing higher gsw becomes more apparent under lower atmospheric humidity owing to higher atmospheric demand. Relative atmospheric humidity (RH) was calculated for a constant temperature of 25 °C. (d) Calculations with the semiempirical model14 under steady-state transpiration and steady-state photosynthesis rates (A) with variable atmospheric humidity (expressed as RH at a constant 25 °C) and variable Dv. The stomatal conductance to CO2 (gsc) was calculated under the assumption that gsw=α·gsc with α=1.6. Simulations were performed for approximate modern and Cretaceous Ca of 350 and 1,000 p.p.m., respectively.
Leaf interior distances for CO2 and water vapour transport
To provide an answer to the question why evolving angiosperms so suddenly increased their leaf gas exchange capacity by increasing Dv beyond the Late Cretaceous maximum, we involve a role for leaf interior water vapour transport in relation to leaf interior CO2 transport. Hereto we calculated the maximum path length for water vapour transport between the leaf vein ending and the stomatal pore (termed the ), and the maximum path length for leaf interior CO2 transport (termed the ). In contrast to the liquid-phase water transport mechanism discussed previously, this approach is based on the mechanism that water evaporates deep inside the mesophyll close to the leaf vein endings34,35,36 and that CO2 experiences an additional resistance by travelling between the stomatal pore and the sites of carboxylation41. When considering this vapour-phase mechanism, the relative distances of and are important because they influence the rate of water vapour and CO2 transport through the intercellular airspaces, and thereby provide a mechanism to alter the tradeoff between water loss and carbon gain. Moreover, diffusion around individual stomata inside the leaf is a three-dimensional process, whereby the driving concentration gradients are altered both by the length of the diffusion path and by the size of the stomatal pore30.
At the basis of our vapour-phase model were our calculations of evolutionary changes in relative to that occurred in angiosperms and conifers during the Cretaceous. For this analysis we used reconstructed ranges in Dv and Ds for Cretaceous angiosperms (Fig. 1d and Supplementary Table S1, respectively) and the schematised leaf morphologies of broad-leaved angiosperms and needle-leaved conifers (Fig. 1e). We note that also leaf thickness is relevant for determining the and , however, this plant trait is problematic to infer from compressed fossil material5. We therefore assumed typical ranges in vein-epidermal distance of 70–130 μm, as commonly applied for modelling leaf gas exchange of Cretaceous species5,14. Details on these calculations are presented in the Supplementary Methods. Our analysis of relative to revealed that a fundamental transition may have occurred in angiosperm leaf evolution at the onset of their global radiation. The critical Dv at which = ranges from 2.5–5 mm mm−2, depending on vein-epidermal distance and Ds (Fig. 3a). The Dv of modern canopy angiosperms in excess of 5 mm mm−2 (cf. Fig. 1d (refs 14,15)) therefore exceeds this critical Dv. Hence, is shorter than in densely veined modern angiosperms. In contrast, the Dv of Early Cretaceous angiosperms of ~1–6 mm mm−2 (refs 5,14,15) lies on or below this critical Dv. Following the evolution in angiosperm leaf venation based on ancestral-state analyses14 for an intermediate vein-epidermal distance of 100 μm indicated that became shorter than before the onset of the angiosperm radiation during the Early Cretaceous (Fig. 3b). Using observations on fossil angiosperm Dv15 for the same calculation revealed a similar pattern that is somewhat delayed relative to ancestral state reconstruction. These fossil data indicated that before the onset of the angiosperm radiation (before 110 Ma), the average was longer than , with an average ratio in / of 1.14 (with standard error of mean, s.e.m.=0.024). At the onset of the escalating rise in angiosperm Dv (between 105 and 98 Ma) the average became shorter than , with an average ratio in / of 0.80 (s.e.m.=0.005). This development continued during the latest Cretaceous and earliest tertiary (77–58 Ma) when was reduced even further to an average ratio in / of 0.62 (s.e.m.=0.003). A similar shift did not occur in the schematised needle leaf as remained longer than due to its central-veined and tubular morphology (Supplementary Fig. S1).
(a) Calculation of the critical Dv for which equalled in the schematised angiosperm leaf morphology. Calculation of the critical Dv used Ds in a range of 30–700 mm−2 as observed in extant relatives of Early Cretaceous angiosperms5 and assuming a typical range in vein-epidermal distance (dyw) of 70 and 130 μm (refs 5,14). Dashed lines indicate crossing of the critical Dv at ~2.5–5 mm mm−2. Approximate ranges of Dv observed in Early Cretaceous angiosperms (1–6 mm mm−2) and modern canopy angiosperms (>5 mm mm−2) (refs 5,14,15) are indicated. (b) Evolutionary changes in the ratio / through time. Calculations are based on angiosperm Dv obtained from fossil leaves15 (circles with error bars) and age-calibrated ancestral-state analyses (grey sigmoid curve)14. The calculations assumed an average Early Cretaceous angiosperm Ds of 116 mm−2 (Supplementary Table S1) and a range in dyw of 70–130 μm (refs 5,14,20), with a highlighted intermediate value of 100 μm. The dashed line indicates the critical ratio /=1. Crossing of this critical ratio occurred during the Early Cretaceous at the onset of the angiosperm radiation. Average values calculated from Dv observed on fossil leaves15 assuming an intermediate dyw of 100 μm for three crucial stages in angiosperm leaf vein evolution are: 1.14 (with s.d., σ=0.36 with n=30 observations) for 132–110 Ma, 0.80 (σ=0.23, n=95) for 105–98 Ma, and 0.62 (σ=0.13, n=90) for 77–58 Ma. Time ranges of these stages are based on the timing of the two-phased escalation of angiosperm Dv15. (c) Surpassing the critical Dv potentially allowed evolving angiosperms to optimize leaf gas exchange and experience a carbon uptake advantage by reducing stomatal pore size. The proposed mechanism is shown by the theoretical relation between diffusive fluxes of substances X and Y (JX and JY) relative to their respective radial diffusion distances (lX and lY) from a single hemispherical pore with variable radius r (equation (14))42.
We hypothesize that surpassing the critical Dv gave evolving angiosperms a competitive advantage over conifers when falling Ca required rising gsmax via increases in Ds and decreases in stomatal pore size. Key to the proposed mechanism is that the tradeoff between CO2 transport and water vapour transport through the leaf interior is altered by differences in and and, considering the three-dimensionality of diffusion, the size of the stomatal pore. This mechanism is illustrated for the diffusive fluxes of two conceptual substances (JX, JY) with equal diffusivity (assumed unity) driven by an equal concentration difference (also assumed unity) over different radial distances (lX and lY) from a single hemispherical pore with variable radius (r) (Fig. 3c), according to equation (14) (ref. 42). The first result shown by this example is that the diffusive flux is highest of that substance, which diffuses over the shortest radial distance. Interpreting this first result for leaf interior fluxes of CO2 and water vapour around individual stomata indicates that the highest carbon flux relative to a water vapour flux can be achieved when is shorter than . This situation would resemble the diffusion distances in the schematised conifer and early angiosperm leaf morphologies (cf. Fig. 1e). The second result of this example is that a change in pore radius has the largest effect on the flux of the substance that diffuses over the shortest radial distance. The physiological implication of this second result is that when <, as in the schematised modern angiosperm leaf morphology, a decrease in pore size leads to a larger decrease in leaf interior water vapour transport than in CO2 transport. On the basis of this mechanism, we propose that when angiosperms surpassed the critical Dv (which rendered <) they could increase leaf interior CO2 transport relative to leaf interior water vapour transport by developing leaves with more and smaller stomatal pores. The consequences of developing leaves with more and smaller stomata not only affected leaf interior gas transport, but also allowed evolving angiosperms to increase gsmax due to the combined implications of Fick’s law and Stefan’s law. Hence, gradually surpassing the critical Dv may have suddenly created an opportunity for evolving angiosperms to increase their stomatal gas exchange capacity.
Leaf interior water vapour transport and photosynthesis
We investigated the hypothesized vapour-phase mechanism with an analytical model of leaf gas exchange, which coupled the diffusion pathways of CO2 and water vapour between the atmosphere and the stomata to their respective diffusion pathways in the leaf interior. A graphical representation of our model approach is shown in Supplementary Fig. S2. We thereby considered the schematised morphologies of needle-leaved conifers and broad-leaved angiosperms (Fig. 1e) to calculate the ratio in / resulting from changes in Dv and Ds. To reveal the subsequent consequences of changes in stomatal pore size and Ds for leaf gas exchange, we solved the model for maximum photosynthetic carbon returns from equal transpirative water loss assuming that water evaporates deep inside the mesophyll near the leaf vein endings34,35,36. This analysis was based on the premise that the maximum water transport capacity of the whole plant constrains the maximum transpiration rate, which in turn determines maximum photosynthesis and productivity in a specific evaporative environment20. Further details on our model approach, including the assumptions and an evaluation with empirical data, are provided in the Supplementary Methods.
Our model showed that the conifer and Early Cretaceous angiosperm leaf morphologies (with >) permit relatively high photosynthesis with equal water loss due to the relatively short distance for CO2 transport and the relatively large distance for water transport inside the leaf (Fig. 4a). A rise in Ds combined with a decrease in stomatal pore size led to diminishing carbon returns with equal water loss for these leaf morphologies. The combined values of Ds and stomatal pore size (expressed as pore radian, rp) used in these simulations are shown in Fig. 4b. In contrast, the angiosperm leaf morphology with Dv beyond the critical density (thus with <) appeared relatively inefficient with low Ds but it may increase photosynthesis with equal water loss by developing leaves with higher Ds and smaller pores. This carbon uptake advantage emerges from the model because, due to the three-dimensional character of diffusion, a development of smaller stomata most strongly reduces the flux of that substance which diffuses over the shortest radial distance around each single pore inside the leaf (Fig. 3c). As we solved our model for an equal water flux, the reduction in stomatal pore size was accompanied by an increase in Ds (Fig. 4b). Important here is to consider that the same values of stomatal pore size and Ds also govern the diffusion of CO2 from the atmosphere into the leaf whereas does not, a priori, equal . Hence, the total leaf conductance to CO2 (gtc), which includes both the stomatal and leaf interior conductance to CO2, is not, a priori, equal to gtw/α. Consequentially, our model revealed that depending on the ratio/, different carbon returns from equal water loss may be found as a function of stomatal pore size and Ds under otherwise equal boundary conditions.
(a) Simulated changes in maximum photosynthesis (A) with equal water loss for the conifer, and the early and modern angiosperm leaf morphologies as a function of stomatal density (Ds). Water use efficiency (WUE) is indicated on the second y axis. Changes in Ds are associated with inverse changes in stomatal pore size to answer a constant water loss of 10 mmol m−2 s−1. Depending on leaf morphology and Dv, changes in Ds and stomatal pore size have different effects on gic and giw, and thereby affect the tradeoff between water loss and carbon gain. Simulations used constant Ca of 1,000 p.p.m. and a constant relative atmospheric humidity of 80% at 25 °C as boundary conditions. (b) Relation between Ds and stomatal pore size (expressed as pore radian, rp) in the simulated stomatal morphologies shown in a. (c) Relation between Ds and the pore size of fully opened stomata (amax) observed in modern angiosperms (blue symbols) and modern conifers (black symbols) from Florida43 and extant relatives of early angiosperms (green symbols)5. Lines of equal maximal stomatal conductance (gsmax) and leaf surface area allocated to fully opened stomatal pores (A%) are indicated. (d) Simulations of the vapour-phase mechanism suggest that angiosperms experienced a shift from falling (phase I) to rising (phase II) photosynthesis with equal water loss by increasing Ds and reducing rp after surpassing the critical Dv. WUE is indicated on the second y axis. Ranges of Dv observed in Early Cretaceous and modern angiosperms15 are also indicated to show that the simulated transition from phase I to phase II matches the divergence observed between Early Cretaceous and modern angiosperm leaf venation. Model boundary conditions are as described for a.
This result revealed that with <, as in the modern angiosperm leaf morphology, a reduction in pore size combined with an increase in Ds may have increased the CO2 flux relative to an equal water vapour flux. As evolution will likely have favoured those individuals that achieve highest carbon returns within the constraint of the whole-plant water transport capacity, we expect to find evidence for the proposed mechanism in observations of Ds and stomatal pore sizes on the leaves of conifers, early angiosperms and modern angiosperms. We therefore compared observations of these stomatal traits of modern conifers and angiosperms from the mid to upper canopy of subtropical forests in Florida43 with observations on extant relatives of Early Cretaceous angiosperms5 (Fig. 4c). Statistical comparisons of stomatal traits between these groups are presented in Supplementary Table S1. These data indicated that modern angiosperms develop leaves with most and smallest stomata of the three groups. The differences in these stomatal properties also showed that the modern angiosperms profit most from the combined implications of Fick's law and Stefan's law and reach highest gsmax. This advantage of developing leaves with many small stomata is illustrated by the solid and dashed lines in Fig. 4c, indicating equal gsmax and the percentage of leaf surface allocated to fully opened stomatal pores (A%), respectively.
A sudden carbon uptake advantage for evolving angiosperms
The proposed ability of angiosperms that surpassed the critical Dv to profit from developing leaves with more and smaller stomata provides a mechanism to explain the revolutionary escalation of angiosperm leaf gas exchange during the Cretaceous. In accordance with fossil evidence15, the proposed mechanism entails that angiosperm evolution occurred in two phases with the first phase linked to Dv rising up to the critical density, and a second phase during which their gas exchange capacity escalated. During the first evolutionary phase, our model revealed that highest carbon returns from equal water loss could be achieved with few and large stomata (Fig. 4d). The second phase started when surpassing the critical Dv rendered <. From that moment onwards, our model revealed that evolving angiosperms could increase photosynthesis with equal water loss by developing leaves with more and smaller stomata. Moreover, the influence of stomatal traits on modelled carbon uptake became larger with higher Dv, which indicates a functional benefit from increasing Dv beyond the Cretaceous maximum of 6–10 mm mm−2. We propose that surpassing the critical Dv may therefore have facilitated evolving angiosperms to develop leaves with more and smaller stomata and more reticulated venation, whereas coniferous species remained to develop less densely veined leaves with relatively few and large stomata.
Discussion
An important concept for the interpretation of these results is the idea that water loss presents a cost to plants. As a result, short-term changes in stomatal aperture are aimed at the optimization of carbon gain with minimal water loss44,45 depending on environmental conditions46. The optimization hypothesis may also explain the adaptation of the stomatal traits governing gsmax at decadal23 or at evolutionary timescales47. On the basis of our results we propose to expand the concept of optimal gas exchange to describe the adjustments of stomatal pore size and Ds in relation to evolutionary adaptations in leaf morphology and venation. Similar to the observations on stomatal traits shown in Fig. 4b, our vapour-phase model suggests that conifers and early angiosperms (with >) may optimize minimal water loss with maximum carbon gain by developing leaves with relatively few and large stomata rather than leaves with more and smaller stomata. Our results also indicate that angiosperms that surpassed the critical Dv (with <) could optimize the tradeoff between carbon uptake and water loss by developing leaves with more and smaller stomata, permitting higher gtc within the constraint of A% (Fig. 5a). As a result of this gas exchange advantage, we propose that angiosperms with Dv beyond the critical density experienced a competitive advantage over angiosperms with lower Dv and coniferous species when an increase gtc was required to prevent carbon ‘starvation’19 during the Cretaceous Ca decline (Fig. 5b). Although these results are based on the concept that water is transported (partly) as a vapour through the intercellular airspaces34,35,36,37, rising Dv likely also facilitated liquid-phase leaf water transport14,20. Potentially, the liquid and vapour-phase mechanisms may have acted in concert, whereby crossing the critical Dv initiated an evolutionary development towards higher gsmax and higher Kleaf. However, the liquid-phase mechanism alone does not provide a clear explanation for the sudden escalation of angiosperm Dv beyond the Cretaceous maximum of ~6–10 mm mm−2 (ref. 28).
(a) Relations between stomatal density (Ds), stomatal pore radius (rp) and total leaf conductance to CO2 (gtc). Proposed directions of stomatal trait optimization are indicated. Values of gtc that require >10% of the leaf surface to be allocated to fully opened stomatal pores (A%) are shaded grey. Highest gtc can only be achieved within the constraint of this A% by developing leaves with high Ds and small rp. Constant relative atmospheric humidity of 80% at 25 °C was used as boundary condition. (b) Falling Ca required a rise in gtc to sustain photosynthesis rates (A). The A is scaled relative to maximum carboxylation rate (Vcmax) as changes in Vcmax likely occurred at geological timescales19. Atmospheric humidity is as in a. (c) Conceptual overview of how crossing of the critical Dv facilitated the Cretaceous angiosperm revolution. Key to the proposed mechanism is that leaf venation and stomatal gas exchange are intrinsically linked20, and that rising stomatal conductance increases the vulnerability to desiccation unless a more extensive leaf water transport system can answer the additional water flux32. As angiosperms exhibited a sudden increase in leaf venation after surpassing the critical Dv, their vulnerability to desiccation (as indicated by the grey surfaces) shows a hump-shaped relationship over time. In contrast, conifers experienced a steady increase in their vulnerability to desiccation as their leaf water transport system evolved only marginally through time14. We suggest that the first phase in angiosperm leaf vein evolution gradually drove angiosperm leaf evolution to a maximum in vulnerability to desiccation. Surpassing the critical Dv then suddenly enabled evolving angiosperms to increase carbon returns from (equal) water loss by developing leaves with more and smaller stomata resulting in higher stomatal conductance. This development facilitated evolving angiosperms to invest in expanding leaf water transport tissue to reduce their vulnerability to desiccation and increase productivity in drier atmospheres, such as the upper canopy. The resulting competitive advantage of angiosperms over conifers may explain their competitive success and rapid speciation during the Cretaceous1,6,7,8.
Considering the proposed vapour-phase mechanism, a positive feedback in angiosperm leaf evolution may emerge from the combined adaptations of stomatal traits and leaf venation because additional carbon uptake can increase growth and productivity. These additional carbon gains may have been invested in expanding leaf water transport tissue to sustain growing transpiration rates. In contrast, if rising stomatal conductance is not supported by an increase in water transport capacity, plants become more vulnerable to desiccation32. The initial phase of gradual leaf vein evolution, potentially related to reducing the carbon cost associated with developing an extensive water transport system12,13, may therefore have suddenly facilitated the rapid evolution of angiosperm leaf venation beyond the critical Dv14,15. The resulting escalation in leaf gas exchange capacity likely permitted evolving angiosperms to leave their original moist niches near the dark forest floor4,5, and become more successful in the drier and brighter upper canopy8. To interpret crossing of the critical Dv as a critical transition48, we argue that gradually reducing beyond provided angiosperms with a sudden carbon uptake advantage over coniferous species during the Cretaceous Ca decline17. As light, CO2 and water are key resources for all plants, the sudden increase in angiosperm leaf gas exchange capacity during the Cretaceous Ca decline may explain their rapid speciation in niches previously dominated by conifers49. Surpassing the critical Dv is therefore proposed to have been the pivotal moment that facilitated the evolutionary rise of angiosperms towards modern biodiversity. This critical transition in angiosperm leaf evolution is shown conceptually in Fig. 5c. Although crossing of the critical Dv may explain the sudden rise in angiosperm leaf gas exchange capacity, the question remains why a similar evolution did not occur in other clades that also evolved planate leaves with diverse venation structures20,29. As leaves with many small stomata and highly reticulated venation provide a clear carbon uptake advantage under low Ca14,24, novel insights may be obtained by unravelling the mechanisms that prevented non-angiosperm clades from evolving these leaf traits.
Methods
Stomatal size, density and conductance relations
The maximal stomatal conductance to water vapour (gsmax) and to CO2 (gcmax) (both with units mol m−2 s−1) were calculated from stomatal properties as24:

and

where and (m2 s−1) are diffusivities of water vapour and CO2, respectively, v (m3 mol−1) is the molar volume of air, Ds is stomatal density (m−2), amax is stomatal pore size with fully inflated guard cells (m2) and pd (m) is pore depth. The amax was calculated from measurements of pore length assuming stomata are ellipse-shaped with pore width equal to half the pore length43. The pd was calculated from species-specific relations with guard cell width for the modern conifers and angiosperms from Florida23,43 and based on measurements for extant relatives of Early Cretaceous angiosperms5. When gsmax was calculated to visualize the scaling with Ds and amax (for example Fig. 4b), the species average relation between guard cell width and pd for the modern conifers and angiosperms was used23. The percentage of the leaf surface area occupied by fully opened stomatal pores (A%) was calculated as:

Photosynthesis
Steady-state photosynthetic carbon returns (A1 (mol m−2 s−1)) were calculated with the biochemical model of Farquhar et al.40 in both the liquid and the gas phase model:

where Ci is the leaf interior CO2 concentration (mol mol−2), cp is the CO2 compensation point (mol mol−1) and the a1 (mol m−2 s−1) and a2 (mol mol−1) are determined by whether photosynthesis is limited by light or by Rubisco. As we assume maximum photosynthesis rates (light saturation), a1 equals the maximum carboxylation capacity  . Here, Kc (mol mol−1) and Ko (mol mol−1) are the Michaelis constants for CO2 fixation and oxygen inhibition, respectively, and the Coa (mol mol−1) is the oxygen concentration in the air. For values of these parameters and their temperature dependencies, we followed Katul et al.45, hence Kc was assumed 300 μmol mol−1, Ko was assumed 300 mmol mol−1 and Coa was assumed 210 mmol mol−1 at a temperature of 25 °C. A constant Vcmax value of 59 mol m−2 s−1 was assumed to represent the maximum carboxylation rate at 25 °C. We note that up and down regulation of Vcmax likely occurred in response to changes in Ca19 and that altered oxygen levels also affected photosynthesis during the Cretaceous50,51. Yet, we assumed constant photosynthesis parameters to allow testing our hypothesis on the effect of stomatal and leaf morphological adaptations on leaf gas exchange.
. Here, Kc (mol mol−1) and Ko (mol mol−1) are the Michaelis constants for CO2 fixation and oxygen inhibition, respectively, and the Coa (mol mol−1) is the oxygen concentration in the air. For values of these parameters and their temperature dependencies, we followed Katul et al.45, hence Kc was assumed 300 μmol mol−1, Ko was assumed 300 mmol mol−1 and Coa was assumed 210 mmol mol−1 at a temperature of 25 °C. A constant Vcmax value of 59 mol m−2 s−1 was assumed to represent the maximum carboxylation rate at 25 °C. We note that up and down regulation of Vcmax likely occurred in response to changes in Ca19 and that altered oxygen levels also affected photosynthesis during the Cretaceous50,51. Yet, we assumed constant photosynthesis parameters to allow testing our hypothesis on the effect of stomatal and leaf morphological adaptations on leaf gas exchange.
Liquid-phase model
Our simulations for liquid-phase water transport were based on a previously published semiempirical model14. This model was parameterized for a broad variety of species, including extant relatives of Early Cretaceous angiosperms, modern angiosperms and conifers14,20. The model relates leaf vein density (Dv (mm mm−2)) to the length of postvenous liquid apoplastic water flow path ( (μm)), leaf hydraulic conductance (Kleaf (mmol MPa−1 m−2 s−1)) and actual stomatal conductance to water vapour (gsw (mol m−2 s−1) according to the following set of equations:




The leaf internal water transport distance parallel to the plane of the leaf (dxw(l) (μm)) was calculated as14:

in which the empirically derived value of 650 accounts for the hierarchical pattern of leaf venation in angiosperm broad leaves14,20. The vein-epidermal distance perpendicular to the plane of the leaf (dyw (μm)) was assumed to be in the range of 70–130 μm, following previous plant physiological modelling work5,14,20,28. The curvature (or turtuosity) of the liquid flow path through the leaf interior (τ) was assumed π/2 following Brodribb et al.20 For the maximum permissible leaf water potential gradient (Δψleaf) we assumed a value of 0.4 MPa, following Brodribb and Feild14. Further, to calculate the difference in water vapour content between the leaf boundary layer (wa (mol mol−1)) and the substomatal cavity (ws (mol mol−1)) we assumed saturation at 25 °C. Assuming steady-state so that the transpirative water vapour flux (E1 (mol m−2 s−1)) equals leaf interior liquid water flow (E2 (mol m−2 s−1), equations (5, 6, 7, 8, 9) can be combined as:

A second expression for the potential maximum photosynthetic carbon return (A2 (mol m−2 s−1)) was calculated from equation (10) under the assumption that gsw=α·gsc,with  :
:

Here, Ca and Ci are the CO2 concentrations in the atmosphere and inside the leaf (mol mol−1), respectively. With Ci being the only unknown in two expressions for carbon uptake (equations 4 and 11), the steady-state photosynthesis rate was obtained by iteratively solving the expression A1=A2 using the software Wolfram Mathematica 7.0 to find the correct Ci with a prescribed Ca.
Vapour-phase model
To solve the equations for leaf gas exchange in our vapour-phase model we simplified equations (1) and (2) by assuming that stomata had circular shapes with radius (rp) and pd equal to ½ rp:

and

It should be noted that stomata are sometimes ellipse or dumbbell-shaped52, which could potentially alter gsmax related to a specific pore length. However, also in these cases diffusion through stomata remains governed by Fick’s law and Stefan's law yielding a similar relation between pore size, Ds and gsmax26,53. Consideration of alternative stomatal shapes would therefore not fundamentally alter our results.
We simulated leaf interior transport of CO2 and water vapour around individual stomata by using the analytical solution of three-dimensional spherical diffusion42. This solution describes the three-dimensional diffusive flux J (mol s−1) of a substance with diffusivity D (m2 s−1) from a single (hemi)spherical pore with radius r (m) over a radial distance l (m) driven by a concentration difference between the pore interior C1 (mol mol−1) and the concentration C2 (mol mol−1) at radial distance l:

The basic results of this equation were presented in Fig. 3c to indicate the scaling of diffusive fluxes of two comparable substances over different distances around a single hemispherical pore of variable size.
The three-dimensional solution for the conductance g3D (mol s−1) over a radial distance (l) from a single hemispherical pore with radius (r) may then be written as:

Prior modelling results30 have indicated that the concentration gradients around the end of the stomatal pore in the leaf interior take the form of a hemisphere with a radius approximately equal to rp. Expanding on these results, we assumed that the CO2 and water vapour concentrations at the end of the stomatal pore equalled the concentrations at the start/end of their respective leaf interior diffusion pathways. Hereby we note that the ‘end correction’ term to account for these spherical diffusion shells around individual stomata was applied to both sides of the stomatal pore in equations 12 and 13 (ref. 27). Hence, we extended the analytical solution of g3D to represent multiple stomata expressed per unit leaf surface area to simulate the leaf interior conductance of CO2 (gic (mol m−2 s−1)) between the end of the stomatal pore and the sites of carboxylation as:

where (m) represents the maximum radial diffusion distance for CO2, η (−) accounts for part of the leaf interior CO2 transport occurring through the mesophyll cells30, and θ (−) and τ (−) denote the porosity and tortuosity of the leaf interior assumed to be ½ and π/2, respectively. Our calculation of and the estimation of the parameter η are presented in the Supplementary Methods.
Similar to the calculation of gic, we calculated the leaf interior (postvenous) conductance of water vapour giw (mol m−2 s−1) over the maximum distance between the leaf vein endings and the stomatal pore (m) as:

Our calculation of is also presented in the Supplementary Methods.
Assuming conservation of mass, the respective transport pathways of CO2 and water vapour across the stomata and through the leaf interior were coupled. This allowed us to express stomatal conductance and leaf interior conductance as a series of resistances, which may be summed up to a single total conductance to CO2 (gtc (mol m−2 s−1)):

and a total conductance to water (gtw (mol m−2 s−1)):

in which fd (−) is a constant compensating for the difference between the geometric maximal stomatal conductance and the actual stomatal conductance during periods of maximum photosynthesis. We assumed fd to be ½ representing plants functioning at a Δψleaf that initiates a 50% reduction in actual stomatal conductance39.
The CO2 transport from the atmosphere to the sites of carboxylation inside the leaf (A3 (mol m−2 s−1)) was then calculated as:

and water vapour transport from the leaf vein endings to the atmosphere E3 (mol m−2 s−1) was calculated as:

The wi (mol mol−1) represented the water vapour concentration in the intercellular airspaces near the leaf vein endings, for which we assumed saturation at a constant temperature of 25 °C.
To obtain the results presented in Fig. 4a, a fixed maximum transpiration rate (E3) of 10 mmol m−2 s−1 was expressed in terms of gtw assuming a constant atmospheric relative humidity of 80% with temperature of 25 °C. As both gtw and gtc are functions of the variables Ds and rp (equations 18 and 19), we expressed gtw in terms of those Ds and rp required to answer the specified E3 (equation 21). With Ci being the only unknown in two expressions for carbon uptake (equations 4 and 20), the steady-state photosynthesis rate was obtained from iteratively solving the expression A1=A3 by finding the correct Ci using the software Wolfram Mathematica 7.0. Photosynthesis could then be expressed as a function of Ds and, for the angiosperm leaf morphology, also as a function of Dv. We note that solving our model for higher constant transpiration rates yielded higher values of gtw, which also yielded higher photosynthesis rates for all leaf morphologies.
Additional information
How to cite this article: de Boer H. J. et al. A critical transition in leaf evolution facilitated the Cretaceous angiosperm revolution. Nat. Commun. 3:1221 doi: 10.1038/ncomms2217 (2012).
References
Crepet W. L., Niklas K. J. Darwin’s second ‘abominable mystery’: Why are there so many angiosperm species? Am. J. Bot. 96, 366–381 (2009)
Darwin C. The Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life ( John Murray (1872)
Friedman W. E. The meaning of Darwin’s ‘abominable mystery’. Am. J. Bot. 96, 5–21 (2009)
Feild T. S., Arens N. C., Doyle J. A., Dawson T. E., Donoghue M. J. Dark and disturbed: a new image of early angiosperm ecology. Paleobiology 30, 82–107 (2004)
Feild T. S. et al. Fossil evidence for low gas exchange capacities for Early Cretaceous angiosperm leaves. Paleobiology 37, 195–213 (2011)
Lidgard S., Crane P. R. Quantitative analyses of the early angiosperm radiation. Nature 331, 344–346 (1988)
Crane P. R., Lidgard S. Angiosperm diversification and paleolatitudinal gradients in cretaceous floristic diversity. Science 246, 675–678 (1989)
Bond W. The tortoise and the hare: ecology of angiosperm dominance and gymnosperm persistence. Biol. J. Linn. Soc. 36, 227–249 (1989)
Dilcher D. Toward a new synthesis: major evolutionary trends in the angiosperm fossil record. Proc. Natl Acad. Sci. USA 97, 7030–7036 (2000)
Berendse F., Scheffer M. The angiosperm radiation revisited, an ecological explanation for Darwin’s ‘abominable mystery’. Ecol. Lett. 12, 865–872 (2009)
Beerling D. J., Franks P. J. Plant science: the hidden cost of transpiration. Nature 464, 495–496 (2010)
McKown A. D., Cochard H., Sack L. Decoding leaf hydraulics with a spatially explicit model: principles of venation architecture and implications for its evolution. Am. Nat. 175, 447–460 (2010)
Blonder B., Violle C., Bentley L. P., Enquist B. J. Venation networks and the origin of the leaf economics spectrum. Ecol. Lett. 14, 91–100 (2011)
Brodribb T. J., Feild T. S. Leaf hydraulic evolution led a surge in leaf photosynthetic capacity during early angiosperm diversification. Ecol. Lett 13, 175–183 (2010)
Feild T. S. et al. Fossil evidence for Cretaceous escalation in angiosperm leaf vein evolution. Proc. Natl Acad. Sci. USA 108, 8363–8366 (2011)
Berner R. A., Kothavala Z. Geocarb III: a revised model of atmospheric CO2 over phanerozoic time. Am. J. Sci. 301, 182–204 (2001)
Fletcher B. J., Brentnall S. J., Anderson C. W., Berner R. A., Beerling D. J. Atmospheric carbon dioxide linked with Mesozoic and early Cenozoic climate change. Nat. Geosci. 1, 43–48 (2008)
Brodribb T. J., Holbrook N. M., Zwieniecki M. A., Palma B. Leaf hydraulic capacity in ferns, conifers and angiosperms: impacts on photosynthetic maxima. New Phytol. 165, 839–846 (2005)
Franks P. J., Beerling D. J. CO2-forced evolution of plant gas exchange capacity and water-use efficiency over the Phanerozoic. Geobiology 7, 227–236 (2009)
Brodribb T. J., Feild T. S., Jordan G. J. Leaf maximum photosynthetic rate and venation are linked by hydraulics. Plan Physiol. 144, 1890–1898 (2007)
Brodribb T. J., McAdam S. A. M. Passive origins of stomatal control in vascular plants. Science 331, 582–585 (2011)
McAdam S. A. M., Brodribb T. J. Stomatal innovation and the rise of seed plants. Ecol. Lett. 15, 1–8 (2012)
de Boer H. J. et al. Climate forcing due to optimization of maximal leaf conductance in subtropical vegetation under rising CO2 . Proc. Natl Acad. Sci. USA 108, 4041–4046 (2011)
Franks P. J., Beerling D. J. Maximum leaf conductance driven by CO2 effects on stomatal size and density over geologic time. Proc. Natl Acad. Sci. USA 106, 10343–10347 (2009)
Fick A. Ueber diffusion. Ann. Phys 170, 59–86 (1855)
Stefan J. Ueber die Verdampfung aus einem kreisförmig oder elliptisch begrenzten Becken. Ann. Phys 253, 550–560 (1882)
Franks P. J., Farquhar G. D. The effect of exogenous abscisic acid on stomatal development, stomatal mechanics, and leaf gas exchange in tradescantia virginiana. Plan Physiol. 125, 935–942 (2001)
Boyce C. K., Zwieniecki M. A. Leaf fossil record suggests limited influence of atmospheric CO2 on terrestrial productivity prior to angiosperm evolution. PNAS 109, 10403–10408 (2012)
Boyce C. K. Patterns of segregation and convergence in the evolution of fern and seed plant leaf morphologies. Paleobiology 31, 117–140 (2005)
Parkhurst D. F. Tansley review no. 65. diffusion of CO2 and other gases inside leaves. New Phytol. 126, 449–479 (1994)
Tholen D., Zhu X.-G. The mechanistic basis of internal conductance: a theoretical analysis of mesophyll cell photosynthesis and CO2 diffusion. Plan Physiol. 156, 90–105 (2011)
Sack L., Holbrook N. M. Leaf hydraulics. Annu. Rev. Plant Boil. 57, 361–381 (2006)
Nonami H., Schulze E.-D. Cell water potential, osmotic potential, and turgor in the epidermis and mesophyll of transpiring leaves. Planta 177, 35–46 (1989)
Boyer J. S. Water transport. Annu. Rev. Plant. Physiol. 36, 473–516 (1985)
Farquhar G. D., Raschke K. On the resistance to transpiration of the sites of evaporation within the leaf. Plant Physiol. 61, 1000–1005 (1978)
Peak D., Mott K. A. A new, vapour-phase mechanism for stomatal responses to humidity and temperature. Plant Cell Environ. 34, 162–178 (2011)
Pieruschka R., Huber G., Berry J. A. Control of transpiration by radiation. Proc. Natl Acad. Sci. USA 107, 13372–13377 (2010)
Noblin X. et al. Optimal vein density in artificial and real leaves. PNAS 105, 9140–9144 (2008)
Brodribb T. J., Holbrook N. M. Stomatal closure during leaf dehydration, correlation with other leaf physiological traits. Plant Physiol. 132, 2166–2173 (2003)
Farquhar G. D., Caemmerer S., Berry J. A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78–90 (1980)
Warren C. R. Stand aside stomata, another actor deserves centre stage: the forgotten role of the internal conductance to CO2 transfer. J Exp Bot 59, 1475–1487 (2008)
Crank J. The Mathematics of Diffusion ( Clarendon Press, Oxford (1979)
Lammertsma E. I. et al. Global CO2 rise leads to reduced maximum stomatal conductance in Florida vegetation. Proc Natl Acad. Sci. USA 108, 4035–4040 (2011)
Mäkelä A., Berninger F., Hari P. Optimal control of gas exchange during drought: theoretical analysis. Ann. Bot. 77, 461–468 (1996)
Katul G., Manzoni S., Palmroth S., Oren R. A stomatal optimization theory to describe the effects of atmospheric CO2 on leaf photosynthesis and transpiration. Ann. Bot. 105, 431–442 (2010)
Manzoni S. et al. Optimizing stomatal conductance for maximum carbon gain under water stress: a meta-analysis across plant functional types and climates. Funct. Ecol. 25, 456–467 (2011)
Roth-Nebelsick A., Grein M., Utescher T., Konrad W. Stomatal pore length change in leaves of Eotrigonobalanus furcinervis (Fagaceae) from the Late Eocene to the Latest Oligocene and its impact on gas exchange and CO2 reconstruction. Rev. Palaeobot. Palynol. 174, 106–112 (2012)
Scheffer M., Carpenter S., Foley J. A., Folke C., Walker B. Catastrophic shifts in ecosystems. Nature 413, 591–596 (2001)
Tilman D. Niche tradeoffs, neutrality, and community structure: a stochastic theory of resource competition, invasion, and community assembly. Proc. Natl Acad. Sci. USA 101, 10854–10861 (2004)
Beerling D. J. Modelling palaeophotosynthesis: Late Cretaceous to present. Philosoph. Transact. 346, 421–432 (1994)
Berner R. A. GEOCARBSULF: a combined model for Phanerozoic atmospheric O2 and CO2 . Geochim. Cosmochim. Acta 70, 5653–5664 (2006)
Franks P. J., Farquhar G. D. The mechanical diversity of stomata and its significance in gas-exchange control. Plant Physiol. 143, 78–87 (2007)
Parlange J.-Y., Waggoner P. E. Stomatal dimensions and resistance to diffusion. Plant Physiol 46, 337–342 (1970)
Acknowledgements
We thank Tim Brodribb, David Dilcher, Peter Franks, Gabriel Katul, Emmy Lammertsma, Max Rietkerk and Rike Wagner-Cremer for their constructive comments on the manuscript. This work was funded by the High Potential programme of Utrecht University.
Author information
Authors and Affiliations
Contributions
H.J.B., S.C.D. and M.J.W. designed the research; H.J.B., S.C.D. and M.B.E. analysed data; H.J.B. and M.B.E. carried out statistical analyses; H.J.B. wrote the manuscript with the help and supervision from M.B.E., S.C.D. and M.J.W.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S3, Supplementary Table S1, Supplementary Methods and Supplementary References. (PDF 663 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
de Boer, H., Eppinga, M., Wassen, M. et al. A critical transition in leaf evolution facilitated the Cretaceous angiosperm revolution. Nat Commun 3, 1221 (2012). https://doi.org/10.1038/ncomms2217
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2217
This article is cited by
-
Revisiting trends in morphology of antennal sensilla in scarabaeoid beetles
Zoomorphology (2022)
-
Integrating stomatal physiology and morphology: evolution of stomatal control and development of future crops
Oecologia (2021)
-
Gymnosperms on the EDGE
Scientific Reports (2018)
-
Proteomics analysis reveals marker proteins for minor vein initiation in rice leaf
Functional & Integrative Genomics (2018)
-
The rise of angiosperm-dominated herbaceous floras: Insights from Ranunculaceae
Scientific Reports (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.