Abstract
Femtosecond magnetization phenomena have been challenging our understanding for over a decade. Most experiments have relied on infrared femtosecond lasers, limiting the spatial resolution to a few micrometres. With the advent of femtosecond X-ray sources, nanometric resolution can now be reached, which matches key length scales in femtomagnetism such as the travelling length of excited 'hot' electrons on a femtosecond timescale. Here we study laser-induced ultrafast demagnetization in [Co/Pd]30 multilayer films, which, for the first time, achieves a spatial resolution better than 100 nm by using femtosecond soft X-ray pulses. This allows us to follow the femtosecond demagnetization process in a magnetic system consisting of alternating nanometric domains of opposite magnetization. No modification of the magnetic structure is observed, but, in comparison with uniformly magnetized systems of similar composition, we find a significantly faster demagnetization time. We argue that this may be caused by direct transfer of spin angular momentum between neighbouring domains.
Similar content being viewed by others
Introduction
The phenomenon of ultrafast demagnetization1, first discovered in 1996, resulting from excitation by an intense femtosecond infrared laser pulse, has been extensively investigated, yet its underlying mechanism remains poorly understood2. Additionally, it has attracted considerable interest as a possible path to magnetization control on a femtosecond timescale3. Most commonly, the magneto-optical Kerr effect (MOKE) is exploited as a femtosecond probe of the temporal evolution of magnetization2. Despite some controversy about the validity of MOKE as a probe of the magnetization of an excited system on the femtosecond timescale4,5,6,7, significant progress has been made: the importance of subtle effects, such as direct transfer of spin angular momentum8 or coherent magneto-optical processes9, have been revealed. Phenomenological and microscopic models have been proposed and further refined10,11,12,13.
However, up to now, ultrafast demagnetization has not been studied at the magnetic domain level itself, owing to the spatial resolution limit set by the infrared laser wavelength of the MOKE probe pulse. Intuitively, this can be seen as one of the limitations of the available experimental data, because the particularities of an underlying magnetic domain structure can have an influence on macroscopic properties of a ferromagnetic material. Moreover, nanometre distances are the relevant length scale for energy and angular momentum transfer occurring on the femtosecond timescale between electrons, spins and the lattice, which are the processes underlying the macroscopically observed ultrafast demagnetization phenomenon. X-rays, with their wavelength of a few nanometres or shorter, potentially offer nanometre spatial resolution in time-resolved experiments.
In this regard, the recent advent of femtosecond-pulsed soft and hard X-ray sources in the form of free-electron lasers14,15 (XFELs), synchrotron radiation femtoslicing16,17 and high-order harmonic generation (HHG)18 sources, has opened up the possibility of novel experiments, which combine, for the first time, femtosecond temporal and nanometre spatial resolution in an element-specific observation of ultrafast dynamics occurring in complex materials. The first time-resolved experiments relying on femtosecond X-ray sources have already led to new insight into ultrafast magnetization dynamics19,20,21,22. Snapshot imaging of nanoscale magnetic structures using a single femtosecond XFEL pulse has also been demonstrated23,24. However, the full potential of these new sources, combining temporal and spatial resolution, had not been exploited so far.
This gap is filled by our study on laser-driven demagnetization in a [Co/Pd]30 multilayer having a nanometric magnetic domain structure. This work fully exploits the capabilities of HHG femtosecond soft X-ray sources by combining, in an infrared pump–X-ray probe experiment, a temporal resolution of about 40 fs with sub-100 nm spatial resolution. Our experiment reveals that locally, within each magnetic domain, the magnetization undergoes a rapid decrease, on the femtosecond timescale, as previously observed macroscopically for uniformly magnetized thin films. The overall magnetic domain structure, on the other hand, retains its organization, even for the highest excitation power accessible in this experiment. Surprisingly, the observed demagnetization times (~100 fs) are shorter than those reported for uniformly magnetized Co compounds. Furthermore, they do not vary with excitation power as suggested by previous work. We postulate that these observations are a consequence of direct transfer of spin angular momentum between neighbouring domains.
Results
Experimental details
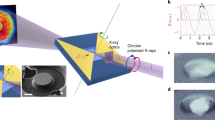
Figure 1a is a schematic representation of the set-up. The static part of the experiment (without infrared pump) has been described in more detail in refs 25,26. In short, femtosecond harmonic pulses are generated in a gas cell, monochromatized at an energy of 60 eV (20.7nm) and focussed onto the sample. This photon energy matches the Co M3 absorption edge, which exhibits a pronounced resonant magneto-optical effect27. As demonstrated previously26,28, this gives rise to magnetic scattering even when using linearly polarized harmonics. A small fraction of the infrared laser beam driving the HHG process is used as a pump initiating the demagnetization dynamics. Because pump and probe pulses originate from the same laser pulse, this set-up is inherently jitter free. This allows us to follow the demagnetization dynamics with a time resolution of about 40 fs (see Methods), which is significantly better than what has been achieved so far in pump-probe experiments at femtoslicing and XFEL sources19,20.
(a) Schematic diagram of the pump–probe set-up. (b) Magnetic force micrograph of the magnetic structure of the sample, a [Co−Pd]30 multilayer film. The white scale bar represents 500 nm. (c) This structure consists of alternating up-and-down magnetic domains aligned along the same direction with an out-of-plane magnetization (white arrows).
The sample used was a 30nm thin [Co(0.4 nm)/Pd(0.6 nm)]30 multilayer film, deposited by magnetron sputtering on a silicon nitride membrane, which exhibits an out-of-plane magnetic anisotropy (Supplementary Fig. S1). A demagnetization procedure was applied29 to prepare a magnetic domain structure of aligned stripes (Fig. 1b,c). This acts as a diffraction grating for the resonant soft X-rays26, giving rise to plus-and-minus first-order diffraction peaks as shown in Fig. 2a. The intensity, I(q), of this resonant elastic magnetic scattering pattern, recorded with an in-vacuum charge-coupled device (CCD) camera, is proportional to |S(q)|2 with q the wave vector transfer and S(q) the Fourier transform of the magnetic domain structure23. The temporal evolution of the scattering pattern thus reveals the evolution of the magnetic domain structure on the nanometre length scale during the demagnetization process. The achievable spatial resolution is in principle only limited by the wavelength employed, and magnetic domains as small as 60 nm are easily detected in our set-up26. Moreover, the integrated diffracted intensity in the first-order peaks is proportional to T and M2, where T is the average transmission of the sample and M the magnetization magnitude within each magnetic domain (Equation (3) and (4)). The film average transmission being constant during the experiment (Supplementary Fig. S2), the magnetization at the magnetic domain level can be retrieved for each delay. We note that in our experiment, the integrated magnetization along the film normal is measured, treating each depth of the film on an equal footing. This is contrary to an optical MOKE experiment, where the sampling depth is set by the penetration of the optical light (15 nm in metallic films).
(a,b) The resonant magnetic scattering patterns exhibit two well-defined bright spots indicating that the magnetic structure of the sample consists of aligned magnetic domains (the scale bars go from 0, white, to 750 CCD counts, orange; 16 CCD counts ~1 detected photon). Whereas the overall pattern remains the same for negative, panel (a), and positive, panel (b), delays, a clear decrease of the integrated intensity can be observed a few hundreds of femtosecond after an optical excitation. (c) Scattered intensity as a function of wave-vector transfer, q, for increasing time delays for a pump fluence of 7.5mJcm−2. The solid lines are fits by the same pseudo-Voigt profile scaled to take into account the evolution of the integrated intensity. The curves exhibit one peak centre at q0=0.04nm−1 with an FWHM, Δq0, of 0.006nm−1 corresponding to a mean magnetic domain width of about 80 nm. The high signal-to-noise ratio of these curves yields a very sensitive probe for the occurrence of spatial variations of the magnetic domain structure during the ultrafast demagnetization process.
Analysis of time-resolved magnetic scattering patterns
Typical scattering patterns (accumulated over 500 s and covering the q-range from 0.01 to 0.12nm−1) obtained at a pump fluence of 7.5mJcm−2 and reproduced in Fig. 2a,b, show clearly the plus-and-minus first order of the magnetic domain grating. As the diffraction efficiency is very small (~10−6)26, a beamstop has to be used to prevent the direct beam from saturating the CCD camera. The two patterns have been recorded for negative (Fig. 2a) and positive (Fig. 2b) time delays of the X-ray probe pulse with respect to the infrared pump pulse. Whereas the overall structure of the two patterns is the same, the decrease in intensity of the diffraction peaks is evident to notice only 100 fs after the infrared pump pulse has been applied. We note that the general structure of the magnetic scattering pattern does not change in this repetitive pump-probe experiment. This suggests that the overall magnetic domain structure recovers after each pump-probe cycle, at least within the statistical description underlying the observed scattering pattern29.
To obtain a detailed view on the spatial evolution of the magnetic domain structure during the demagnetization process, we perform radial and azimuthal integration of the scattering pattern I(q). In Fig. 2c, radial intensity profiles are plotted for different pump-probe time delays. The relation between real space distances,  and wave vector transfer, q, is given by equation (1). A comparison of these curves reveals that peak position and shape remain unchanged. In particular, independently of the applied pump-probe delay, one does not observe any additional scattering at higher q values, which would correspond to breaking-up of magnetic domains in smaller ones. An absence of any variations with pump-probe delay is also observed when comparing the azimuthal integrals of I(q) (Supplementary Fig. S3), which indicates that the alignment of the magnetic domains remains unchanged. We can thus conclude that the magnetic stripe domain pattern does remain unchanged during the demagnetization process, with a mean domain width of 2π/q0 (~80nm) and an in-plane correlation length of 2π/Δq0 (~1μm).
and wave vector transfer, q, is given by equation (1). A comparison of these curves reveals that peak position and shape remain unchanged. In particular, independently of the applied pump-probe delay, one does not observe any additional scattering at higher q values, which would correspond to breaking-up of magnetic domains in smaller ones. An absence of any variations with pump-probe delay is also observed when comparing the azimuthal integrals of I(q) (Supplementary Fig. S3), which indicates that the alignment of the magnetic domains remains unchanged. We can thus conclude that the magnetic stripe domain pattern does remain unchanged during the demagnetization process, with a mean domain width of 2π/q0 (~80nm) and an in-plane correlation length of 2π/Δq0 (~1μm).
The evolution of the local magnetization amplitude is revealed by the peak intensity of the radial integrals shown in Fig. 2c. It reproduces the general behaviour previously observed for transition metal-based ferromagnetic materials2, namely, a very fast initial demagnetization on the timescale of a few hundred femtoseconds followed by a slow partial recovery. This behaviour is described by the phenomenological three temperature model proposed for uniformly magnetized films1. The electronic system is heated by the optical excitation almost instantaneously. Its energy is rapidly transferred to the spin system causing the initial rapid demagnetization. The subsequent thermalization of the electron and spin system with the lattice results in a partial recovery of the magnetization. On a longer timescale (a few nanoseconds), the three subsystems cool down because of heat transfer to the surrounding material, and the magnetization recovers completely. How exactly these processes occur at the microscopic level is still actively debated2,13. In our experiment, the initial heating of the spin system seems to be very fast, because within the first 100 fs, more than two-thirds of the magnetic scattering signal is lost.
Figure 3 shows the magnetization (M normalized to the unpumped magnetization, M0) as a function of time delay for a series of increasing pump fluences. The solid lines reproduce fits by a double exponential expression (Equation (2)) to the data (triangles) based on a semi-empirical model (see Methods), which allows us to extract parameters like the maximum demagnetization, the thermalization time (τth) and the relaxation time from the spin degrees of freedom to others (τs−ph)20. To obtain accurate values for τs−ph, long-delay scans have been performed (Fig. 3b). The thermalization time can also be characterized11 by the delay time τM at which the drop in magnetization reaches 63% of its maximum. The values of τth and τM obtained for the different infrared pump fluence levels are summarized in Table 1. The uncertainty on these values is lower than ±25fs (Supplementary Table S1). One notes that the values of τth are fluctuating within 10 fs around 100 fs with no clear fluence dependance. τM appears also to be fluence independent and equal to 85 fs, although a slow increase with increasing fluence cannot be ruled out. A demagnetization of almost 45% (Fig. 3c) is achieved in the case of the highest fluence level used (11 mJ cm−2), which is just under the destruction threshold of the sample in our repetitive kilohertz experiment. Nevertheless, even for this rather high degree of demagnetization, compared with other studies, we do not observe an increase of the thermalization time.
(a) Demagnetization curves obtained for different pump fluences: 4, 6, 7.5 and 9 mJ cm−2 (respectively; red, up; green, down; cyan, right; and purple, left triangles). The probe fluence, 5×10−5 mJ cm−2, is negligible compared with the pump fluence26. The solid lines represent the best fits obtained for each fluence. The characteristic thermalization times, τth, found are all between 90 and 110 fs with an error of ±25 fs. No clear relation between the pump fluence and τth has been observed. (b) Example of a long delay scan used to determine the spin-phonon relaxation constant, τs−ph. Long delay scans have been performed for each fluence. (c) High-resolution demagnetization curve obtained for the highest possible pump fluence (11 mJ cm−2), yielding a demagnetization of 44% and clearly showing a thermalization time of ~100 fs. The red solid lines in panels (b) and (c) represent the best fits obtained. The dashed lines in panels (a) and (c) indicate the demagnetization times, τth, of about 100 fs.
Discussion
The observation of a short thermalization time, which in addition is independent of the degree of stimulated demagnetization, is rather surprising, considering the results of recent MOKE studies of ultrafast demagnetization in Co-based materials11,30. These studies have reported thermalization times (τM) in the range of 150 to 300fs for demagnetization degrees from 15 to 50% (Supplementary Fig. S4). Moreover, those results agree well with the electron—phonon-mediated spin-flip scattering model developed by Koopmans et al. for the description of the demagnetization process11. One might be tempted to explain this discrepancy by the presence of Pd in the sample. Indeed, the large spin–orbit coupling of Pd could enhance the spin-flip rate thus leading to a shorter thermalization time in our Co/Pd multilayer. This conclusion is, however, in contradiction with the results obtained by Boeglin and co-workers on a 15 nm thin Co0.5Pd0.5 alloy film20 saturated in an external magnetic field. Employing X-ray magnetic circular dichroism absorption spectroscopy in a transmission experiment, these authors determined an overall thermalization time, τth, of about 280 fs, which is in close agreement with the MOKE results mentioned above. We note that X-ray magnetic circular dichroism originates from the same resonant magneto-optical effect as the contrast mechanism in our scattering experiment. Boeglin et al.20 exploited ×it at the Co L2,3 absorption edge, whereas the Co M3 edge was used here. Furthermore, we can rule out the small structural difference between the alloy and our multilayer film as the origin of the difference in thermalization time. Indeed, the difference is minimal as the Co-layer thickness is only 0.4 nm. We confirmed this by repeating our experiment on such a CoPd alloy film (see ref. 26 for film details), which yielded an equally faster demagnetization time (Fig. 4).
Demagnetization curves obtained on a 50nm thin CoPd alloy film26 for a pump fluence of 6 (green downward triangles) and 9mJ cm−2 (red upward triangles). The solid lines represent the best fits. The corresponding parameters are reported in Supplementary Table S2.
To explain the faster demagnetization time observed here, four more experimental differences can be considered: the different probe photon energies used; the thickness of the magnetic layer; the presence or absence of an externally applied, static magnetic field; and the presence of a microscopic magnetic domain structure. The first point can be ruled out rather safely as it would be unreasonable to expect that the photon energies resonant with the Co M edge give shorter relaxation times than the both higher (Co L edge) and lower photon energies (infrared/visible; see Supplementary Fig. S4)11,20. We can equally rule out an effect of film thickness, since comparable thermalization times have been reported for Co-based films with thicknesses ranging from 15 to 110 nm11,30,31. The third point cannot be ruled out completely. We note, however, that MOKE studies have been performed in the presence and absence of an external magnetic field (in fact, complete time-resolved hysteresis loops were recorded1) without revealing a difference in the thermalization time between these two modes.
We are thus left with the last point, the presence of a nanometric magnetic domain structure in our experiment as origin of the observed faster thermalization time. This idea is supported by the recent publication of Malinowski et al.8 These authors noticed that in a magnetic bilayer, spaced by a thin non-magnetic conductive layer, the demagnetization seems to be faster for an antiparallel orientation of the magnetization directions in the two layers. This led them to conclude that the laser-induced demagnetization process could be sped up by direct transfer of spin angular momentum between the two magnetic layers8. The magnetic domain structure of our sample can be seen as a network of such junctions. A direct transfer of spin angular momentum between neighbouring domains would then lead to an acceleration of the demagnetization process. We remark that the efficiency of this angular momentum transfer, and hence the magnitude of the demagnetization, depends on the number of excited carriers (hot electrons). The speed of the transfer, on the other hand, does primarily depend on the specific properties of the junctions. Thus, a thermalization time mostly independent of the degree of demagnetization would then be expected.
The proposed mechanism is further supported by the theoretical work of Battiato et al.12, who show that spin-polarized transport of hot electrons from a magnetic layer to a metallic buffer may account for the early stage of ultrafast demagnetization. It seems natural to extend this theory to the case here, where transport would occur between neighbouring domains with opposite spin-polarization of their majority electrons. We note that, in comparison to typical velocities of hot electrons (up to 1nmfs−1 (ref. 12)) the domain width (~80 nm) is reasonably small. After a few tens of femtoseconds, a significant exchange of spin-polarized electrons from neighbouring domains could have occurred, in line with our observation. We note that the proposed transport of spin-polarized electrons should induce changes in the domain walls between the neighbouring domains. Such changes could be resolved by recording higher diffraction orders or by direct time-resolved imaging of the magnetic domain structure, but neither was possible in the current experimental set-up.
In summary, for the first time, laser-induced demagnetization was studied at the magnetic domain level with a time resolution of about 40 fs and a spatial resolution better than 100nm, thus exploiting the unique capabilities of soft X-ray HHG sources. It has been shown that magnetic domains exhibit locally a rapid loss of magnetization on the femtosecond timescale similar to the one observed in uniformly magnetized transition metal films studied so far. The magnetic domain structure itself remains mostly unaffected by the demagnetization process. A thermalization time of about 100 fs has been revealed, which is faster than has been reported previously11,20. In addition, we do not find any fluence level dependence of the demagnetization process for the range of 14 to 44% of total demagnetization. We provide evidence that the presence of the magnetic domain structure is potentially the origin of these observations via direct transfer of spin angular momentum between neighbouring domains.
Methods
Sample preparation
The sample is a [Co(0. 4 nm)/Pd(0.6 nm)]30 multilayer deposited by magnetron sputtering on a 30-nm thin Si3N4 multi-membranes (squares of 50×50 μm2) chip. This multilayer exhibits an out-of-plane magnetic anisotropy. To enhance heat dissipation, a 30-nm thick Al buffer layer was used and to avoid oxidation a 2-nm thick Pd cap layer was added. The sample is demagnetized so as to present an aligned stripe domain state with an in-plane oscillating magnetic field29.
Pump–probe experiment
The pump–probe set-up is based on a Ti:sapphire laser (λ0=815 nm), delivering 5 mJ, 40 fs (full-width at half-maximum (FWHM)), linearly polarized (horizontal) pulses at 1 kHz. Each pulse is split into a strong part and a weak part (pump) by a 90–10% beam splitter. The strong part is focussed into a gas cell filled with neon (35 mbar) to generate high harmonics (probe) by nonlinear interaction between the laser and the gas. The generated harmonics retain the polarization of the infrared laser and span a wide photon energy range between 40 and 78 eV (ref. 25). Tuning the source parameters allows optimizing the efficiency for the generation of the thirty-ninth harmonic, which matches the Co M3 absorption edge located at 60 eV (ref. 26). To suppress the incident infrared light, a 200nm thick aluminum foil is introduced into the optical path. The transmitted harmonics are then focussed (focal spot of 30 μm in diameter) by a spherical mirror (focal length, 625 mm) coated with a wide-band-gap multilayer onto the sample. To select only the thirty-ninth harmonic, a second multilayer mirror, located a few centimetres before the sample, is used. The pump beam goes through a delay line (step size of 3 fs) and is focussed (focal spot of 150 μm in diameter) to excite the sample. The fluence of the pump beam can be adjusted and the size of the focal spot ensures an uniform illumination across one membrane. The harmonic light, elastically scattered by the magnetic domain structure of the sample, is collected by a PI-MTE CCD camera (Princeton Instrument) located 4 cm behind the sample and protected from any diffuse infrared light by an aluminum filter. This foil is supported by an Ni mesh that appears as a grid on the scattering patterns. The CCD pixels have been binned 4 by 4 yielding a pixel size of 54 μm. The time resolution of this experiment is less than 45 fs (FWHM), which is set predominantly by the infrared pulse duration (40 fs), because the harmonic pulses are much shorter32,33 and because there is no jitter between infrared and harmonic pulses in this set-up.
Data analysis
Resonant magnetic scattering pattern were recorded for different time delays and pump fluences. These patterns are similar to what is expected from incoherent small angle X-ray scattering, although we are using a coherent X-ray beam. However, the speckles due to the coherence are too small to be observed because of the large illuminated area yielding incoherent-like scattering patterns. The charge scattering of diffuse X-rays, due to the square shape of the membrane, is partially blocked by the beam-stop and completely removed for data analysis. For radial integration of the scattering pattern, a recording time of 500 s was necessary whereas a 50s recording time was sufficient to obtain the demagnetization curves. The radial analysis was conducted by measuring the integrated intensity in ring with increasing radius, r, in pixels. Knowing the distance between the sample and the CCD camera, D=40 mm, the size of the pixels, 0.054 mm, and the wavelength of the light, λ=20.7 nm, the data were converted into wave-vector transfer, q, in nm−1, according to the following relation:

The data were then fitted by a pseudo-Voigt profile (often used in X-ray scattering experiments). The demagnetization curves were obtained by summing the intensities of each pixel in the two scattering spots to obtain the integrated density that is proportional to the square of the magnetization (see below). Variations of the harmonic intensity yields a standard deviation of 2% for an integration time of 50 s. The data were then fitted by the following double exponential expression:

where G(t) is the Gaussian function, H(t) is the Heavyside function and τth and τs−ph are, respectively, the thermalization time and the relaxation time from spins to other degrees of freedom5,20. This fit neglects the cooling down of the lattice system, which occurs on the nanosecond timescale and is thus of no relevance on the timescale studied here.
Relation between magnetization and integrated intensity
At a resonant energy, owing to magneto-optical effect, the magnetic domain structure can be approximated by a square grating whose transmission alternates between t+ and t− for up-and-down magnetic domains. The diffracted intensity in the first order, I, of such a grating is given by34:

where n±,  is the optical index of up (+) and down (−) magnetic domains35, d is the thickness of the film and, λ is the wavelength of the radiation. Developing expression 3, we find that I is proportional to
is the optical index of up (+) and down (−) magnetic domains35, d is the thickness of the film and, λ is the wavelength of the radiation. Developing expression 3, we find that I is proportional to  where T is the average transmission of the grating. Given that Δδ and Δβ are both proportional to the magnetization M (ref. 35), it follows:
where T is the average transmission of the grating. Given that Δδ and Δβ are both proportional to the magnetization M (ref. 35), it follows:

Additional information
How to cite this article: Vodungbo, B. et al. Laser-induced ultrafast demagnetization in the presence of a nanoscale magnetic domain network. Nat. Commun. 3:999 doi: 10.1038/ncomms2007 (2012).
References
Beaurepaire, E., Merle, J.- C., Daunois, A. & Bigot, J.- Y. Ultrafast spin dynamics in ferromagnetic nickel. Phys. Rev. Lett. 76, 4250–4253 (1996).
Kirilyuk, A., Kimel, A. V. & Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 82, 2731–2784 (2010).
Stanciu, C. D. et al. All-optical magnetic recording with circularly polarized light. Phys. Rev. Lett. 99, 047601 (2007).
Koopmans, B., van Kampen, M., Kohlhepp, J. T. & de Jonge, W. J. M. Ultrafast magneto-optics in nickel: magnetism or optics? Phys.Rev. Lett. 85, 844–847 (2000).
Guidoni, L., Beaurepaire, E. & Bigot, J.- Y. Magneto-optics in the ultrafast regime: thermalization of spin populations in ferromagnetic films. Phys. Rev. Lett. 89, 017401 (2002).
Zhang, G. P., Hubner, W., Lefkidis, G., Bai, Y. & George, T. F. Paradigm of the time-resolved magneto-optical kerr effect for femtosecond magnetism. Nat. Phys. 5, 499–502 (2009).
Carva, K., Battiato, M. & Oppeneer, P. M. Is the controversy over femtosecond magneto-optics really solved? Nat. Phys. 7, 665–665 (2011).
Malinowski, G. et al. Control of speed and efficiency of ultrafast demagnetization by direct transfer of spin angular momentum. Nat. Phys. 4, 855–858 (2008).
Bigot, J.- Y., Vomir, M. & Beaurepaire, E. Coherent ultrafast magnetism induced by femtosecond laser pulses. Nat. Phys. 5, 515–520 (2009).
Zhang, G. P., Bai, Y. & George, T. F. Energy- and crystal momentum-resolved study of laser-induced femtosecond magnetism. Phys. Rev. B 80, 214415 (2009).
Koopmans, B. et al. Explaining the paradoxical diversity of ultrafast laser-induced demagnetization. Nat. Mater. 9, 259–265 (2010).
Battiato, M., Carva, K. & Oppeneer, P. M. Superdiffusive spin transport as a mechanism of ultrafast demagnetization. Phys. Rev. Lett. 105, 027203 (2010).
Fähnle, M. & Illg, C. Electron theory of fast and ultrafast dissipative magnetization dynamics. J. Phys. Condens. Matter 23, 493201 (2011).
Tiedtke, K. et al. The soft X-ray free-electron laser FLASH at DESY: beamlines, diagnostics and end-stations. New J. Phys. 11, 023029 (2009).
Emma, P. et al. First lasing and operation of an angstrom-wavelength free-electron laser. Nat. Photon. 4, 641–647 (2010).
Schoenlein, R. W. et al. Generation of femtosecond pulses of synchrotron radiation. Science 287, 2237–2240 (2000).
Khan, S., Holldack, K., Kachel, T., Mitzner, R. & Quast, T. Femtosecond undulator radiation from sliced electron bunches. Phys. Rev. Lett. 97, 074801 (2006).
L'Huillier, A. & Balcou, P. High-order harmonic generation in rare gases with a 1-ps 1053-nm laser. Phys. Rev. Lett. 70, 774–777 (1993).
Stamm, C. et al. Femtosecond modification of electron localization and transfer of angular momentum in nickel. Nat. Mater. 6, 740–743 (2007).
Boeglin, C. et al. Distinguishing the ultrafast dynamics of spin and orbital moments in solids. Nature 465, 458–461 (2010).
Radu, I. et al. Transient ferromagnetic-like state mediating ultrafast reversal of antiferromagnetically coupled spins. Nature 472, 205–208 (2011).
La-O-Vorakiat, C. et al. Ultrafast demagnetization dynamics at the M edges of magnetic elements observed using a tabletop high-harmonic soft X-ray source. Phys. Rev. Lett. 103, 257402 (2009).
Gutt, C. et al. Single-pulse resonant magnetic scattering using a soft X-ray free-electron laser. Phys. Rev. B 81, 100401 (2010).
Wang, T. et al. Femtosecond single-shot imaging of nanoscale ferromagnetic order in CoPd multilayers using resonant X-ray holography. Phys. Rev. Lett. 108, 267403 (2012).
Vodungbo, B. et al. Polarization control of high order harmonics in the EUV photon energy range. Opt. Express 19, 4346–4356 (2011).
Vodungbo, B. et al. Table-top resonant magnetic scattering with extreme ultraviolet light from high-order harmonic generation. Europhys. Lett. 94, 54003 (2011).
Valencia, S., Gaupp, A., Gudat, W. & Mertins, H. et al. Faraday rotation spectra at shallow core levels: 3p edges of Fe, Co, and Ni. New J. Phys. 8, 254 (2006).
Eisebitt, S. et al. Polarization effects in coherent scattering from magnetic specimen: implications for X-ray holography, lensless imaging, and correlation spectroscopy. Phys. Rev. B 68, 104419 (2003).
Hellwig, O., Denbeaux, G., Kortright, J. & Fullerton, E. E. X-ray studies of aligned magnetic stripe domains in perpendicular multilayers. Physica B 336, 136–144 (2003).
Wüstenberg, J.- P. et al. Ultrafast magnetization dynamics in the half-metallic heusler alloy Co2Cr0.6Fe0.4Al. Phys. Status Solidi B 248, 2330–2337 (2011).
Steil, D. et al. Band-structure-dependent demagnetization in the heusler alloy Co2Mn1−xFexSi. Phys. Rev. Lett. 105, 217202 (2010).
Mairesse, Y. et al. High harmonic XUV spectral phase interferometry for direct electric-field reconstruction. Phys. Rev. Lett. 94, 173903 (2005).
Papalazarou, E. et al. Probing coherently excited optical phonons by extreme ultraviolet radiation with femtosecond time resolution. Appl. Phys. Lett. 93, 041114 (2008).
Goodman, J. W. Introduction to Fourier Optics (Roberts & Company Publishers, Englewood, 2005).
Kortright, J. B. & Kim, S.- K. Resonant magneto-optical properties of Fe near its 2p levels: measurement and applications. Phys. Rev. B 62, 12216–12228 (2000).
Acknowledgements
We gratefully thank Grégory Malinowski for fruitful discussions and Franck Fortuna for access to AFM/MFM. We acknowledge financial support from the Triangle de la physique (contracts IMMAGE and POL-IMMAGE), from the French Agence Nationale de la Recherche (ANR) under grant NT09491966 (FEMTO-X-MAG) 'Nanoscale imaging of femtosecond magnetization dynamics by scattering of coherent soft X-ray laser harmonics' and from the FCT Portuguese Foundation for Science and Technology. R.H., B.T. and K.L. thank the European Commission for Postdoctoral and Doctoral fellowships through Erasmus Mundus program.
Author information
Authors and Affiliations
Contributions
B.V. and J.L. conceived the experiment. B.V. and J.G. designed the experiment. B.V. analysed the data and wrote the manuscript, with comments from J.G., G.L., P.Z. and J.L. The harmonic beamline was designed by J.G., G.L. and P.Z., with contribution from B.V. B.V., J.G., G.L., A.B.S. and K.L. carried out the experiment. B.T., M.T., R.H. and R.D. deposited and characterized the multilayer samples. V.L.-F., J.A. and C.B. deposited and characterized the alloy sample. M.L. operated the infrared laser. M.D. and W.B. characterized the wavelength dependence of the magnetic scattering. J.L., P.Z. and S.S. supervised the project. J.L., P.Z. and H.M. coordinated research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S4 and Supplementary Tables S1-S2 (PDF 612 kb)
Rights and permissions
About this article
Cite this article
Vodungbo, B., Gautier, J., Lambert, G. et al. Laser-induced ultrafast demagnetization in the presence of a nanoscale magnetic domain network. Nat Commun 3, 999 (2012). https://doi.org/10.1038/ncomms2007
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2007
This article is cited by
-
Mechanism of femtosecond laser induced ultrafast demagnetization in ultrathin film magnetic multilayers
Journal of Materials Science (2022)
-
Ultrafast high-harmonic nanoscopy of magnetization dynamics
Nature Communications (2021)
-
Spin-current-mediated rapid magnon localisation and coalescence after ultrafast optical pumping of ferrimagnetic alloys
Nature Communications (2019)
-
Single-shot Monitoring of Ultrafast Processes via X-ray Streaking at a Free Electron Laser
Scientific Reports (2017)
-
Widely tunable two-colour seeded free-electron laser source for resonant-pump resonant-probe magnetic scattering
Nature Communications (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.