Abstract
Nanophotonics and metamaterials have revolutionized the way we think about optical space (ɛ,μ), enabling us to engineer the refractive index almost at will, to confine light to the smallest of the volumes, and to manipulate optical signals with extremely small footprints and energy requirements. Significant efforts are now devoted to finding suitable materials and strategies for the dynamic control of the optical properties. Transparent conductive oxides exhibit large ultrafast nonlinearities under both interband and intraband excitations. Here we show that combining these two effects in aluminium-doped zinc oxide via a two-colour laser field discloses new material functionalities. Owing to the independence of the two nonlinearities, the ultrafast temporal dynamics of the material permittivity can be designed by acting on the amplitude and delay of the two fields. We demonstrate the potential applications of this novel degree of freedom by dynamically addressing the modulation bandwidth and optical spectral tuning of a probe optical pulse.
Similar content being viewed by others
Introduction
The continual success of electronics is largely due to the extreme miniaturization of devices and the ability to achieve exceptional functionality with a limited number of constituent materials. Currently, these areas are major weaknesses of photonics, which hinder the primary advantage of increased operational bandwidth1,2,3. Specifically, the diffraction limit sets the minimum size of photonic components to about half their operational wavelength, while a plethora of photonic materials are needed to accomplish all the basic functionalities typically available in electronics. During the past decade, plasmonics and metamaterials have both gained great momentum because they provide a way to overcome the previously mentioned limitations. This is attained by coupling the electromagnetic radiation to the oscillating electronic plasma at the metal/dielectric interface4,5. However, the ability to squeeze optical modes well below the diffraction limit, and engineer the effective permittivity at will with structured materials is not free. By tightly confining light to metal layers, the propagation losses are increased, which can be problematic for many applications6. To solve these relevant technological drawbacks, new material platforms have been recently investigated with the goal of removing metal constituents from both plasmonic technologies and artificial materials7,8.
Among alternative plasmonic materials, transparent conductive oxides (TCOs) are a unique class of wide-bandgap semiconductors. They can support extremely large doping levels (≃1021 cm−3) with low effective electron masses (≃0.3me; me=free-electron-mass), enabling a metallic response in the near-infrared (NIR) region and high transmission in the visible region8,9,10,11,12. Such materials have been employed as transparent electrodes in various applications13,14, but are recently receiving attention in nanophotonics, owing to their highly tunable static properties and potential for both electrical and optical control of the refractive index15,16,17,18,19,20,21. This versatility is extremely attractive as TCOs can serve multiple roles, for example as dynamic, plasmonic and dielectric layers, which enable extreme flexibility to optimize structures for differing conditions, all with a single material. Furthermore, many TCOs are naturally suited to achieve the epsilon-near-zero22 condition in the telecommunications band whereby the low refractive index, that is, less than unity, enables the potential for enhanced nonlinearities, super-coupling and deeply subwavelength field confinement19,23,24,25,26,27,28. Aluminium-doped zinc oxide (AZO)12 is one such material which combines all of these properties with reduced optical losses compared to other TCOs8 and a low manufacturing cost due to its widely available elemental compounds. Consequently, oxygen-deprived AZO (see ‘Methods’ section) is an attractive material for dynamic control. The optical injection of carriers into the conduction band (interband excitation in the ultraviolet spectral region, λultraviolet=325 nm) enabled control of the reflection and transmission up to 40% and 35%, respectively, with sub-picosecond recovery time18. Intraband excitations with below-bandgap pulses (in the NIR spectral region, λNIR=787 nm) resulted in up to 90% and 800% modulation of the reflection and transmission, respectively.
Here we demonstrate that the optical properties of AZO can be dynamically addressed on a sub-picosecond timescale by a clever combination of the interband and intraband nonlinear effects, driven by two different wavelength pump pulses (λultraviolet=262 nm and λNIR=787 nm). We first show that the AZO complex refractive index at infrared wavelengths (λp=1,300 nm) can be controlled by a two-colour pump pulse (λultraviolet+λNIR). We then tune the delay between the two pumps to demonstrate the dynamic control of the probe modulation bandwidth, between 0.8 and 2 THz, and optical spectrum with a wavelength shift of ±4 nm.
Results
Pump and probe experiments
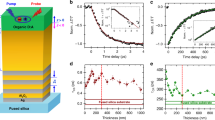
The pump–probe experiment is schematically shown in Fig. 1a. See ‘Methods’ section for details on the experimental settings. We measure the probe pulse transmission (T) and reflection (R) from a 900 nm thick AZO film deposited on a 1 mm thick silica substrate. The probe pulse wavelength is set to λp=1,300 nm, close to the zero-epsilon wavelength of the material. Both T and R are recorded as a function of the delay Δτ between the pump pulses and the probe. In Fig. 1b, we show the measured delay-dependent reduction of transmissivity as a result of interband carrier excitation, driven by an ultraviolet pulse (λultraviolet=262 nm) of ≃65 fs duration and fluence Fultraviolet≃5 mJ cm−2. The recombination time (≃600 fs) and modulation amplitude (≃45%) are consistent with previous measurements performed with a pump pulse at 325 nm (ref. 18). In Fig. 1c, we show the measured delay-dependent increase of transmissivity due to intraband carrier excitation, driven by a 100 fs near-infrared pulse (λNIR=787 nm) with fluence FNIR≃16 mJ cm−2. This metal-like nonlinearity is the result of thermal smearing of free electrons causing decreased absorption and reflection at the probe wavelength and exhibits an extremely fast decay rate of ≃170 fs. As shown by the dotted curves in Fig. 1b,c, the interband and intraband material responses can be successfully modelled using a Drude model coupled to the excess carrier population and the two-temperature model, respectively (see ‘Methods’ section).
(a) Schematic of the two-colour pump–probe experimental set-up where the two pump wavelengths, 787 nm (NIR) and 262 nm (ultraviolet), are illustrated along with the probe wavelength of 1,300 nm. The delay between the two pump pulses is denoted Δt while the delay between the probe and ultraviolet signal is denoted Δτ. For intraband excitation using only the NIR pump, Δτ is defined as the delay between the probe and NIR pump pulse arrival time. The black arcs indicate the arrival time of the pulses. (b) Change in transmission at 1,300 nm versus the pump–probe delay Δτ under 262 nm excitation fitted with simulation. The inset illustrates the process diagram for interband excitation: ultraviolet light (Eultraviolet) generates electron–hole pairs (δn, δp) above the Fermi level (Ef) in addition to the intrinsic concentration (Ni), which recombine through mid-gap trap states (Nt,τrec). (c) Change in transmission at 1,300 nm versus the pump–probe delay Δτ under 787 nm excitation fitted with simulation. The inset illustrates the process diagram for intraband excitation: NIR light (ENIR) raises the temperature of conduction band electrons (Tcool→Thot), which relax through scattering processes (τe−p), heating the lattice. The change in transmission from the experiment was obtained through ΔT=(T−T0)/T0, where T0 is the transmission of the probe far from the pump pulse. For comparison with the theoretical results, the amplitude of the induced transmission change was normalized using ΔTnormalized=ΔT/|ΔTmax|, where |ΔTmax| is the magnitude of the peak change in transmission. The same procedure was completed for the simulation results.
Remarkably, AZO shows simultaneously strong ultrafast interband and intraband nonlinearities with wavelengths readily available from a single laser source.
The observed co-existence of both intraband and interband nonlinearities suggests the possibility of achieving new dynamic functionalities through their combined effect and if these two excitation regimes are independent, the corresponding effects can be algebraically combined. We therefore performed a thorough investigation of the AZO optical response under combined ultraviolet and NIR excitation as a function of the relative delay Δt between the two pumps and Δτ between the pumps and the probe (the ultraviolet pump signal is used as the time reference). From the recorded probe reflection and transmission as a function of the two delays, Rp(Δt, Δτ) and Tp(Δt, Δτ), respectively (see Supplementary Fig. 1), we retrieve the real and imaginary refractive index of the film using a transfer matrix approach, as described elsewhere29. The extracted values are shown in Fig. 2, where the time-dependent relative change in the real (Fig. 2a–e) and imaginary (Fig. 2f–j) refractive index of the AZO film at 1,300 nm is shown, for five values of the NIR–ultraviolet pump pulse delay, between Δt=−1.7 ps and Δt=1.8 ps. The results in Fig. 2 are achieved with optical pump fluences of Fultraviolet=5 mJ cm−2 and FNIR=14 mJ cm−2.
Percentage change of the real (a–e) and imaginary (f–j) part of the refractive index as a function of the delay Δτ between the ultraviolet pump and the infrared probe pulses. Multiple vertical plots are shown, for different delay Δt between the ultraviolet and the NIR pump pulses. Shaded areas indicate whether the ultraviolet pump, which is used as time reference, precedes (light blue) or follows (light red) the NIR pump. Overlapping the results obtained by simultaneous two-colour pumping (red curves), we plot the computed change in refractive index calculated by the algebraic summation of the results obtained from experiments with separate ultraviolet and NIR pump pulses (black dashed curves). The probe, the NIR and the ultraviolet pump wavelengths were set to 1,300 nm, 787 nm and 262 nm, respectively. The probe intensity was low: Ip≃200 MW cm−2, while the pump fluences were Fultraviolet=5 mJ cm−2 and FNIR=14 mJ cm−2.
Our measurements demonstrate that the temporal dynamics of AZO film properties, such as reflection and transmission, or equivalently the real and imaginary part of the refractive index, can be optically controlled via a two-colour excitation scheme. This is enabled by the independence of the two nonlinear processes responsible for the modulation of the material properties. This independence is demonstrated by the good match of the red and the black dashed curves in Fig. 2. The former are obtained from the measurements with simultaneous ultraviolet and NIR excitation while the latter are generated by the algebraic addition of the time-dependent refractive index changes induced by the ultraviolet and NIR pumps independently.
It is worth mentioning that all the experiments are performed in a condition of balanced excitation, meaning that the adopted fluences for ultraviolet and NIR pumping were set in such a way to produce similar alterations (in amplitude but not in sign) on the transmitted power. Operatively speaking, we first arbitrarily choose a fluence for the ultraviolet beam while the NIR pump fluence is set afterwards, to induce a change on the transmitted power of the same magnitude as that obtained with the ultraviolet pump. Such a change saturates for both ultraviolet (ΔT/T0≃75% at Fultraviolet≃15 mJ cm−2) and NIR (ΔT/T≃100% at FNIR≃60 mJ cm−2) pumping.
While cross-coupling between interband and intraband effects is negligible at the pump fluences used in these experiments, we observed that it becomes appreciable for higher fluences. To evaluate the impact of crosstalk, we calculate the relative difference between the measured (me) and ideal (id) change in the real and imaginary refractive index  for increasing pump fluences. In this case, ‘measured’ refers to the refractive index with the simultaneous pumping scheme while ‘ideal’ refers to the algebraic sum of the refractive indices retrieved with independent ultraviolet and NIR excitations. In the experimental conditions of Fig. 2, we estimate Dr≤6 % and Di≤3 %, whereas at higher pump fluences Fultraviolet=10 mJ cm−2 and FNIR=24 mJ cm−2 we observe stronger crosstalk: Dr≤22 % and Di≤7 % (see Supplementary Note 1 and Supplementary Fig. 2).
for increasing pump fluences. In this case, ‘measured’ refers to the refractive index with the simultaneous pumping scheme while ‘ideal’ refers to the algebraic sum of the refractive indices retrieved with independent ultraviolet and NIR excitations. In the experimental conditions of Fig. 2, we estimate Dr≤6 % and Di≤3 %, whereas at higher pump fluences Fultraviolet=10 mJ cm−2 and FNIR=24 mJ cm−2 we observe stronger crosstalk: Dr≤22 % and Di≤7 % (see Supplementary Note 1 and Supplementary Fig. 2).
Modulation bandwidth and wavelength control
The ability to optically control the AZO properties with nonlinear effects of similar amplitude yet opposite sign paves the way to intriguing applications. In Fig. 3, we show two new effects enabled by the two-colour AZO modulation. The first, in Fig. 3a,b, is the dynamic control of the optical modulation bandwidth of the AZO film, while the second, in Fig. 3c,d, is the dynamic control of the transmitted probe wavelength.
(a) Change in the probe pulse transmission as a function of the pump–probe delay (Δτ) and the inter-pump delay (Δt). The ultraviolet (UV) pump decreases the transmission, whereas the NIR increases it. The combined effect produces a Δt-dependent modulation. The modulation bandwidth is evaluated by performing a Fourier transform along Δτ, and is shown by the black curve in b. For delays close to Δt=0, the modulation bandwidth can be decreased or increased by the two-colour combined effect. The blue and red dashed lines show the bandwidth of the ultraviolet-only and NIR-only driven modulation. (c) Measured central wavelength shift of the transmitted probe pulse (≃15 nm bandwidth) in a zoomed Δt−Δτ region (square box in a). The ultraviolet pump blue shifts the probe wavelength, whereas the NIR pump does the opposite. At Δt≃0, the opposite effects almost entirely cancel the wavelength shift. (d) Summary of the findings in c, showing the maximum positive (Δλ+) and negative (Δλ−) wavelength shift for the NIR-only (red dashed/dotted), ultraviolet-only (blue dashed/dotted) and two-colour (solid black) AZO excitation.
All-optical modulation of infrared radiation is relevant to the development of future telecommunications and data networks technologies30,31,32. An ultrafast, >1 THz modulation bandwidth of AZO via interband pumping has been recently reported18. Figure 3a shows the change in T of the AZO film pumped by both ultraviolet and NIR light, resolved as a function of the inter-pump delay Δt and the pump–probe delay Δτ. The effect of the ultraviolet pump is to reduce the transmission (the horizontal blue and purple band), while the effect of the NIR pump is to increase the transmission (the diagonal, green-to-red band). Performing the Fourier transform along the vertical direction provides the modulation bandwidth of the optically excited film as a function of the inter-pump delay Δt and is shown in Fig. 3b. The blue and red dashed lines indicate the bandwidth (rms) obtained by only ultraviolet and only NIR pump, respectively. The faster dynamic of the intraband (≃1.7 THz) compared to the interband (≃1.55 THz) nonlinearity is clear. The proposed two-colour pump configuration remarkably allows one to modify the modulation bandwidth of the film via the delay of the two pump fields, as shown by the black curve in Fig. 3b. This enables the observation of a fast oscillation between a reduction (≃0.75 THz at Δt≃0) and an increase (≃2 THz at Δt≃130 fs) of the bandwidth, although with a fourfold reduction in the modulation depth compared to larger delays.
Further, we show how the probe wavelength can be dynamically modified by a combination of the two ultraviolet and NIR pump pulses. In Fig. 3c, we show the change in the central wavelength of the λp≃1,300 nm probe pulse, recorded with an InGaAs spectrometer, as a function of both Δt and Δτ and for pump fluences Fultraviolet=22 mJ cm−2 and FNIR=42 mJ cm−2. We note that the wavelength shift induced by the ultraviolet pump is negative, while the NIR pump gives both a positive and negative shift, depending on the delay with the probe. Figure 3d shows the maximum positive (Δλ+) and negative (Δλ−) frequency shift induced by the ultraviolet and NIR pumps alone (blue and red curves, respectively) and combined (black curves). Interestingly, the wavelength shift induced by the two independent excitation mechanisms can also be algebraically added. Therefore, for a specific choice of the pump fluences, the wavelength shift is almost cancelled when the two pump pulses are temporally overlapped. We note that, for higher pump fluences, wavelength shifts exceeding the pulse bandwidth can be achieved.
Discussion
AZO features both an interband and intraband transition at wavelengths that are different enough to separate the two effects, yet close enough to be addressed simultaneously by frequency conversion of standard laser sources. This is in contrast with most metals and semiconductors where the nonlinearities are either spectrally overlapped (metals), difficult to access (deep ultraviolet), or spaced too far apart to enable their combined use (semiconductors). However, the observed properties are not unique to AZO, rather a common feature to the class of TCOs. In fact, we observe similar behaviours, that is, the co-existence of interband and intraband nonlinearities with opposite optical effects, in commercially available indium tin oxide films (see Supplementary Note 2 and Supplementary Fig. 3). Although a thorough comparative analysis of the two TCOs goes beyond the purposes of this work, oxygen-deprived AZO shows stronger and faster temporal dynamics. Therefore, it is one of the best options for applications relying on the proposed hybrid nonlinearity at telecom wavelengths.
To conclude, we highlight that the large and dynamically addressable modulation of the AZO refractive index with terahertz bandwidths is a new photonic capability that may lead to interesting developments in signal processing, ultrafast optics and optical metrology. For example, it may enable complex coding schemes such as code division multiple access33, which is of high interest for optical communication. Similarly, engineering the recombination rate to match the thermal relaxation rate of the intraband excitation may lead to the implementation of an all-optical XOR gate via two-colour excitation. Finally, the observed ultrafast and controllable wavelength shift may lay the basis for a novel class of ultrafast and compact optical routers.
Methods
Pump–probe experiment
For the experiment, we relied on a Ti:Sapphire laser (Amplitude Technologies), which delivered up to 10 mJ energy pulses at 787 nm central wavelength, with 100 fs pulse duration. A fraction of the laser power was routed to a commercial white light seeded optical parametric amplifier (Topas, Light Conversion Ltd), which produced the short (<120 fs) probe pulse at a wavelength tunable between 1,100 and 2,600 nm. For the experiments, we controlled the wavelength in the 1,250–1,350 nm range. The s-polarized probe beam was spatially filtered, reduced in energy with neutral density filters and focused by a 250 mm focal length lens onto the AZO film, at a small angle to the normal of the film surface (<10°). The probe beam waist on the sample was measured using the knife-edge technique to be 65 μm. The probe intensity in the focus was found to be 200 MW cm−2, determined by measuring the pulse energy and duration. The probe pulse delay from the pump pulses was set by a computer-controlled linear translation stage (M-VP-25XA, Newport), equipped with a gold-coated hollow retroreflector (PLX Inc.).
The ultraviolet pulse (262 nm) was produced by pumping an in-line third-harmonic generation set-up (Femtokit, Eksma Optics) with ≃1 mJ, 787 nm pulses. The output 200 μJ, ≃65 fs, 262 nm pulses were cleaned from the residual 787 and 393 nm radiation using four dichroic mirrors (HR at 266 nm, HT at 400 and 800 nm, Layertec GmbH). The s-polarized ultraviolet pulse was focused at normal incidence with an f=250 mm focal length CaF2 lens. The beam size measured with a knife-edge was 400 μm. The ultraviolet energy was controlled by acting on the half-wave plate at the input of the third-harmonic generation tool. The NIR pump was obtained by splitting a portion of the laser beam and delaying it from the ultraviolet pulse using a computer-controlled linear translation stage (M-VP-25XA, Newport), equipped with a silver-coated hollow retroreflector (PLX Inc.). The s-polarized NIR pump was focused at normal incidence onto the AZO film. A dichroic mirror (HR at 266 nm, HT at 800 nm, Layertec GmbH) was employed for combining the two pump pulses. The beam waist of the NIR pump was measured to be 210 μm using the knife-edge technique. The pulse energy was controlled with a waveplate in front of a thin-film polarizer (Altechna).
The ultraviolet, NIR and probe energies were measured with a thermopile detector (XPL12, Gentec-EO). The reflected and transmitted signals were recorded with amplified Germanium photodetectors (PDA50B-EC, Thorlabs).
Sample fabrication and characterization
The oxygen-deprived AZO films were deposited using pulsed laser deposition (PVD Products Inc.) with a KrF excimer laser (Lambda Physik GmbH) operating at a wavelength of 248 nm for source material ablation. A 2 wt% doped AZO target was purchased from the Kurt J. Lesker Corp. with a purity of 99.99% or higher. The energy density of the laser beam at the target surface was maintained at 1.5 J cm−2 and the deposition temperature was 75 °C. We maintained the oxygen pressure under 0.01 mTorr to achieve additional free carriers from the oxygen vacancies. The prepared thin films were characterized by spectroscopic ellipsometry (J.A. Woollam Co. Inc.) in the spectral region from 300 to 2,500 nm. The dielectric function of the AZO was retrieved by fitting a Drude (when ωo=0) and Lorentz oscillator model, equation (1), to the ellipsometry data. The optical properties at 262 nm were estimated from a spline extrapolation of the measured properties combined with bounds provided by data from similar films34. To probe the electrical properties of thin films, such as mobility and carrier concentration, we carried out the Hall measurement (MMR Technologies) at room temperature.

Interband dynamics and modelling
The interband modulation, Ehν>Eg, and relaxation of the AZO film were first observed individually using only the 262 nm ultraviolet pump and probe. The sub-picosecond recombination time is indicative of Shockley–Read–Hall recombination processes, which result in a reduced recombination time according to τrec∝1/Ntσνth, where Nt is the trap density, σ is the capture cross section and νth is the thermal velocity of carriers35. The interband dynamics were modelled using a 2D spatial and temporal discretization (see Supplementary Discussion for details).
The change in the optical properties was then determined using the transfer matrix method for the graded index profile whereby a matrix was calculated for each layer δz and multiplied to determine an effective transfer matrix at each time step assuming an infinite substrate of fused silica. The amplitude of the change was then normalized and the recombination rate was fitted to the experimental data. Subsequently, the recombination time of the film was estimated to be ≃600 fs.
Intraband dynamics and modelling
The intraband dynamics, Ehν>Eg of the AZO film were also observed individually using only the 787 nm excitation and probe. At 787 nm, the AZO is a lossy dielectric, but the excitation is still far from the band-edge (λ≃320 nm). Subsequently, the absorption in this regime is dominated by the residual Drude loss, that is, free carriers in the conduction band. This excitation results in a non-equilibrium hot electron population, which relaxes through various scattering processes (τe−p), heating the lattice. Consequently, the intraband dynamics of the AZO film were modelled using the two-temperature model, whereby the change in the electron temperature and lattice temperature are captured as a function of time for the material (see Supplementary Discussion for details). Following, the resulting change in the optical properties was modelled using an effective thermally dependent complex index, nth, such that ΔnAZO=(ΔTe+ΔT1)nth. The transfer matrix method was used to determine the change in the optical properties of the graded index material. The reflection and transmission of the sample were normalized, and the rate was fitted to extract the electron phonon-coupling coefficient and found to be G≃1.41016 W K−1 m−3. After the normalization procedure, only the sign of the complex effective thermal index is relevant, and it was found that the extinction coefficient decreases while the index increased, that is, nth>0 and kth<0, matching the experimental results. However, unlike other materials, we did not observe a long-lasting thermal offset arising from heat dissipation and removal from the lattice. This is likely due to the significant disparity between the electron and lattice heat capacities of AZO (see Supplementary Discussion). Thus, for a small application of energy, the electron temperature increases significantly, giving rise to a large nonlinear response and an observable change in the reflection/transmission, although this energy does not result in a substantial increase in the lattice temperature.
Data availability
All relevant data present in this publication can be accessed at http://dx.doi.org/10.17861/8f45636c-0560-427b-992e-87ba6d9090ab.
Additional information
How to cite this article: Clerici, M. et al. Controlling hybrid nonlinearities in transparent conducting oxides via two-colour excitation. Nat. Commun. 8, 15829 doi: 10.1038/ncomms15829 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
01 August 2017
An incorrect version of the Supplementary Information was inadvertently published with this Article, where the pump wavelengths for panels a and b were interchanged in the figure caption of Supplementary Fig. 3. The HTML has now been updated to include the correct version of the Supplementary Information.
References
Barnes, W. L., Dereux, A. & Ebbesen, T. W. Surface plasmon subwavelength optics. Nature 424, 824–830 (2003).
Brongersma, M. L. & Shalaev, V. M. The case for plasmonics. Science 328, 440–441 (2010).
Kinsey, N., Ferrera, M., Shalaev, V. M. & Boltasseva, A. Examining nanophotonics for integrated hybrid systems: a review of plasmonic interconnects and modulators using traditional and alternative materials. J. Opt. Soc. Am. B 32, 121 (2015).
Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings. Springer Tracts in Modern Physics 111, Springer Berlin Heidelberg (1988).
Maier, S. A. Plasmonics: Fundamentals and Applications Springer (2007).
Khurgin, J. B. & Boltasseva, A. Reflecting upon the losses in plasmonics and metamaterials. MRS Bull. 37, 768–779 (2012).
Blaber, M. G., Arnold, M. D. & Ford, M. J. A review of the optical properties of alloys and intermetallics for plasmonics. J. Phys. Condens. Matter 22, 143201 (2010).
Naik, G. V., Shalaev, V. M. & Boltasseva, A. Alternative plasmonic materials: beyond gold and silver. Adv. Mater. 25, 3264–3294 (2013).
Rhodes, C. et al. Surface plasmon resonance in conducting metal oxides. J. Appl. Phys. 100, 54905 (2006).
Franzen, S. Surface plasmon polaritons and screened plasma absorption in indium tin oxide compared to silver and gold. J. Phys. Chem. C 112, 6027–6032 (2008).
Noginov, M. A. et al. Transparent conductive oxides: plasmonic materials for telecom wavelengths. Appl. Phys. Lett. 99, 21101 (2011).
Naik, G. V., Liu, J., Kildishev, A. V., Shalaev, V. M. & Boltasseva, A. Demonstration of Al:ZnO as a plasmonic component for near-infrared metamaterials. Proc. Natl Acad. Sci. 109, 8834–8838 (2012).
Li, Y. & Ong, B. S. Thin film transistor using an oriented zinc oxide layer. EU patent EP1921681 A2 (2008).
Schmidt, H. et al. Efficient semitransparent inverted organic solar cells with indium tin oxide top electrode. Appl. Phys. Lett. 94, 243302 (2009).
Traviss, D., Bruck, R., Mills, B., Abb, M. & Muskens, O. L. Ultrafast plasmonics using transparent conductive oxide hybrids in the epsilon-near-zero regime. Appl. Phys. Lett. 102, 121112 (2013).
Park, J., Kang, J.-H., Liu, X. & Brongersma, M. L. Electrically tunable epsilon-near-zero (ENZ) metafilm absorbers. Sci. Rep. 5, 15754 (2015).
Huang, Y.-W. et al. Gate-tunable conducting oxide metasurfaces. Nano Lett. 16, 5319–5325 (2016).
Kinsey, N. et al. Epsilon-near-zero Al-doped ZnO for ultrafast switching at telecom wavelengths. Optica 2, 616 (2015).
Caspani, L. et al. Enhanced nonlinear refractive index in ɛ-near-zero materials. Phys. Rev. Lett. 116, 233901 (2016).
Alam, M. Z., De Leon, I. & Boyd, R. W. Large optical nonlinearity of indium tin oxide in its epsilon-near-zero region. Science 352, 795–797 (2016).
Guo, P. et al. Large optical nonlinearity of ITO nanorods for sub-picosecond all-optical modulation of the full-visible spectrum. Nat. Commun. 7, 12892 (2016).
Alù, A., Silveirinha, M. G., Salandrino, A. & Engheta, N. Epsilon-near-zero metamaterials and electromagnetic sources: tailoring the radiation phase pattern. Phys. Rev. B 75, 155410 (2007).
Silveirinha, M. G. & Engheta, N. Theory of supercoupling, squeezing wave energy, and field confinement in narrow channels and tight bends using ɛ near-zero metamaterials. Phys. Rev. B 76, 245109 (2007).
Schuller, J. A. et al. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 9, 193–204 (2010).
Abb, M., Albella, P., Aizpurua, J. & Muskens, O. L. All-optical control of a single plasmonic nanoantenna-ITO hybrid. Nano Lett. 11, 2457–2463 (2011).
Luk, T. S. et al. Enhanced third harmonic generation from the epsilon-near-zero modes of ultrathin films. Appl. Phys. Lett. 106, 151103 (2015).
Tyborski, T. et al. Ultrafast nonlinear response of bulk plasmons in highly doped ZnO layers. Phys. Rev. Lett. 115, 147401 (2015).
Capretti, A., Wang, Y., Engheta, N. & Dal Negro, L. Enhanced third-harmonic generation in Si-compatible epsilon-near-zero indium tin oxide nanolayers. Opt. Lett. 40, 1500 (2015).
Kaipurath, R. M. et al. Optically induced metal-to-dielectric transition in epsilon-near-zero metamaterials. Sci. Rep. 6, 27700 (2016).
Fang, X. et al. Ultrafast all-optical switching via coherent modulation of metamaterial absorption. Appl. Phys. Lett. 104, 141102 (2014).
Lee, H. W. et al. Nanoscale conducting oxide plasmostor. Nano Lett. 14, 6463–6468 (2014).
Melikyan, A. et al. High-speed plasmonic phase modulators. Nat. Photon. 8, 229–233 (2014).
Haffner, C. et al. All-plasmonic Mach-Zehnder modulator enabling optical high-speed communication at the microscale. Nat. Photon. 9, 525–528 (2015).
Kim, J. et al. Optical properties of gallium-doped zinc oxide—a low-loss plasmonic material: first-principles theory and experiment. Phys. Rev. X 3, 41037 (2013).
Neamen, D. A. Semiconductor Physics and Devices 4th edn. McGraw-Hill Education (2003).
Acknowledgements
This work was supported by the NSF MRSEC Grant DMR-1120923, AFOSR Grant FA9550-14-1-0138 and AFOSR Grant FA9550-14-1-0389. D.F. acknowledges financial support from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC GA 306559 and EPSRC (UK, Grant EP/M009122/1). M.C. acknowledges support from EPSRC (Grants No. EP/P009697/1 and EP/P51133X/1) and from BLM s.p.a. L.C. acknowledges the support from the People Programme (Marie Curie Actions) of the European Union’s FP7 Programme under REA Grant Agreements No. 627478 (THREEPLE). M.F. acknowledges sponsorship from EPSRC (UK, Grant EP/P019994/1). The authors thank Prof. Arrigo Calzolari, CNR Nano Modena Italy, for helpful discussions during the development of numerical models.
Author information
Authors and Affiliations
Contributions
M.C., E.G.C., L.C., D.F. and M.F. contributed to the optical characterization and measurements. N.K., C.D., J.K., A.S., V.S. and A.B. contributed to the material development and modelling. All the authors contributed to the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Notes, Supplementary Figures, Supplementary Discussion and Supplementary References (PDF 796 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Clerici, M., Kinsey, N., DeVault, C. et al. Controlling hybrid nonlinearities in transparent conducting oxides via two-colour excitation. Nat Commun 8, 15829 (2017). https://doi.org/10.1038/ncomms15829
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms15829
This article is cited by
-
Engineering the temporal dynamics of all-optical switching with fast and slow materials
Nature Communications (2023)
-
Integrated metasurfaces for re-envisioning a near-future disruptive optical platform
Light: Science & Applications (2023)
-
Intensity and wavelength-dependent two-photon absorption and its saturation in ITO film
Applied Physics A (2023)
-
Thickness-dependent nonlinear optical properties of ITO thin films
Optical and Quantum Electronics (2023)
-
Near-zero-index ultra-fast pulse characterization
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.